
Мокрoусов_ПЗ_Криптопротоколы
.pdfФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра систем информационной безопасности
281 - 2014
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям по дисциплине «Криптографические протоколы»
для студентов специальности 090301 «Компьютерная безопасность»,
очной формы обучения
Воронеж 2014
Составитель канд. техн. наук А. Н. Мокроусов
УДК 681.326
Методические указания к практическим занятиям по дисциплине «Криптографические протоколы» для специальности 090301 «Компьютерная безопасность» очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. А. Н. Мокроусов. Воронеж, 2014, 44 с.
Методические указания предназначены для студентов четвертого и пятого курсов, выполняющих практические занятия по изучению основ криптографии. Рассмотрены основные методы шифрования данных.
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2013 и содержатся в файле Мокроусов_ПЗ_Криптопротоколы.pdf.
Ил. 9. Табл. 3. Библиогр.: 10 назв.
Рецензент д-р техн. наук, проф. А. Г. Остапенко
Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. А. Г. Остапенко
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУ ВПО «Воронежский государственный технический университет», 2014
Практическая работа № 1 Шифрование данных в группе симметричных
блочных алгоритмов REDOC
Цель работы: изучить методы шифрования данных в алгоритмах REDOC и освоить их практическое применение.
Теоретическое введение
REDOC представляет собой группу симметричных блочных алгоритмов, в которой используются 20-байтовый (160-битовый) ключ и 10 байтный (80-битовый) блок.
В алгоритме REDOC II все манипуляции - перестановки, подстановки и XOR (логическое исключающее ИЛИ) выполняются с байтами ключа, а не с битами как во многих других алгоритмах. Эта особенность позволяет его эффективно реализовать программно. В REDOC II используются переменные табличные функции. В REDOC II используются зависимые от ключа и открытого текста наборы таблиц (по сути, S-блоки). В REDOC II 10 этапов, каждый этап представляет собой сложную последовательность манипуляций с 10-байтовым блоком.
Другой уникальной особенностью является использование масок, которые являются числами, полученными из таблицы ключей, и используются для выбора таблиц данной функции для данного этапа. Для выбора таблиц функции используются как значение данных, так и маски.
Алгоритм REDOC III
Существует значительно упрощенная версия алгоритма REDOC II - REDOC III, созданная Майклом Вудом. Используется также 80-битный блок, длина ключа переменна, может достигать 2560 байт (20480 бит). Перестановки и подстановки исключены, все операции над блоком и ключом основаны лишь на применении XOR, за счет чего значительно
увеличена скорость шифрования в ущерб стойкости к дифференциальному криптоанализу. Основой алгоритма являются генерированные на основе секретного ключа 256 10байтовых ключей, и полученные на основе XOR 128 10байтовых ключей и два 10-байтовых блока маски. Для успешного восстановления обеих масок алгоритма REDOC III требуется 223 открытых текстов.
Алгоритм зашифрования REDOC III
1)Создать таблицу ключей из 256 10-байтовых ключей, используя секретный ключ.
2)Создать два 10-байтовых блока маски M1 и M2, где M1 представляет собой XOR первых 128 10-байтовых ключей,
аM2 - XOR вторых 128 10-байтовых ключей.
3)Для шифрования 10-байтового блока:
а) Выполнить XOR для первого байта блока данных и первого байта M1. Выбрать ключ из таблицы ключей, рассчитанной на 1 этапе, используя вычисленное значение в качестве индекса таблицы. Выполнить XOR каждого, кроме первого, байта блока данных с соответствующим байтом выбранного ключа.
б) Выполнить XOR для второго байта блока данных и второго байта M1. Выбрать ключ из таблицы ключей, рассчитанной на 1 этапе, используя вычисленное значение в качестве индекса таблицы. Выполнить XOR каждого, кроме второго, байта блока данных с соответствующим байтом выбранного ключа.
в) Продолжать для всего блока данных (для байтов с 3 по 10), пока каждый байт не будет использован для выбора ключа из таблицы после выполнения для него XOR с соответствующим значением M1. Затем выполнить XOR с ключом для каждого, кроме использованного для выбора ключа, байта.
г) Повторить для M2 этапы (а) – (в).
2
Создание таблицы ключей
Таблица ключей, используемая в алгоритме шифрования REDOC III, строится на основании секретного ключа и генератора псевдослучайных чисел (ГПСЧ).
Заполнение таблицы осуществляется циклически и состоит из 35 шагов.
На каждом шаге объединяются пары двух символов секретного ключа по порядку в одно 2 байтовой значение, причем одна пара за один шаг. Полученное значение используется для инициализации ГПСЧ.
После того, как ГПСЧ инициализирован, производится циклическое заполнение таблицы ключей, состоящей из 2560 элементов. Каждый последующий элемент является псевдослучайным числом, сгенерированным ГПСЧ. Сгенерированное число записывается по индексу k n, где k – номер шага заполнения, а n – простое число, выбранное из табл.1 по номеру шага создания таблицы ключей.
|
|
|
|
|
|
Таблица 1 |
|
1 |
3 |
5 |
7 |
11 |
13 |
|
17 |
19 |
23 |
29 |
31 |
37 |
41 |
|
43 |
47 |
53 |
59 |
61 |
67 |
71 |
|
73 |
79 |
83 |
89 |
97 |
101 |
103 |
|
107 |
109 |
113 |
127 |
131 |
137 |
139 |
|
149 |
Алгоритм расшифрования REDOC III
Алгоритм расшифрования заключается в последовательном выполнении описанных в алгоритме зашифрования действий.
1)Создать таблицу ключей из 256 10-байтовых ключей, используя секретный ключ.
2)Создать два 10-байтовых блока маски M1 и M2, где M1 представляет собой XOR первых 128 10-байтовых ключей,
аM2 - XOR вторых 128 10-байтовых ключей.
3
3) Для расшифрования 10-байтового блока:
а) Выполнить XOR для десятого байта блока данных и десятого байта M2. Выбрать ключ из таблицы ключей, рассчитанной на 1 этапе, используя вычисленное значение в качестве индекса таблицы. Выполнить XOR каждого, кроме десятого, байта блока данных с соответствующим байтом выбранного ключа.
б) Выполнить XOR для девятого байта блока данных и девятого байта M2. Выбрать ключ из таблицы ключей, рассчитанной на 1 этапе, используя вычисленное значение в качестве индекса таблицы. Выполнить XOR каждого, кроме девятого, байта блока данных с соответствующим байтом выбранного ключа.
в) Продолжать для всего блока данных (для байтов с 8 по 1), пока каждый байт не будет использован для выбора ключа из таблицы после выполнения для него XOR с соответствующим значением M2. Затем выполнить XOR с ключом для каждого, кроме использованного для выбора ключа, байта.
г) Повторить для M1 этапы (а) – (в).
Задание:
Используя алгоритм шифрования данных REDOC, написать программу шифрования и дешифрования произвольного набора символов на любом языке программирования.
Порядок выполнения работы:
написать на языке программирования функцию шифрования, в которую в качестве параметров передается ключ и символ (или строка символов) исходного текста.
написать функцию дешифрования, в которую в качестве параметров передается ключ и символ (или строка символов) зашифрованного текста.
4
Оформление отчета:
В отчете следует привести краткие теоретические сведения. Кроме того, должны быть представлены: краткая блок-схема, текст программы, шифруемый набор символов, результаты выполнения программы.
Контрольные вопросы:
1.В чем заключается суть метода шифрования
REDOC?
2.Какой характерной особенностью обладает
REDOC III?
3.Что используется в качестве таблицы ключей?
4.Поясните общую схему симметричного шифрования.
5.Что общего имеют все методы шифрования с закрытым ключом?
6.Назовите основные группы методов шифрования с закрытым ключом.
7.Приведите примеры шифров перестановки.
8.Сформулируйте общие принципы для методов шифрования подстановкой.
5
Практическая работа № 2 Шифрование данных с помощью генератора Геффе
Цель работы: изучить методы шифрования данных в алгоритме Геффе и освоить их практическое применение.
Теоретическ ое введение
В этом генераторе потока ключей используются три LFSR, объединенные нелинейным образом. Два LFSR являются входами мультиплексора, а третий LFSR управляет выходом мультиплексора. Если а1, а2 и а3 - выходы трех LFSR, выход генератора Геффе можно описать как:
b = (a1 ^ a2) XOR ((¬a1) ^ a3)
Если длины LFSR равны n1, n2 и n3, соответственно, то линейная сложность генератора равна
(n1 + 1)n2 + n1n3
Период генератора равен наименьшему общему кратному периодов трех генераторов. При условии, что степени трех примитивных многочленов обратной связи взаимно просты, период этого генератора будет равен произведению периодов трех LFSR. Этот генератор криптографически слаб и не может устоять против корреляционного вскрытия. В 75 процентах времени выход генератора равен выходу LFSR-2.
Поэтому, если известны отводные последовательности обратной связи, можно догадаться о начальном значении LFSR-2 и сгенерировать выходную последовательность этого регистра. Тогда можно подсчитать, сколько раз выход LFSR совпадает с выходом генератора. Если начальное значение определено неверно, две последовательности будут согласовываться в 50 процентах времени, а если правильно, то в 75 процентах времени.
6
С такими корреляциями генератор потока ключей может быть легко взломан. Например, если примитивные многочлены состоят только из трех членов, и длина самого большого LFSR равна n, для восстановления внутренних состояний всех трех LFSR нужен фрагмент выходной последовательности длиной 37n битов.
Обобщенный генератор Геффе
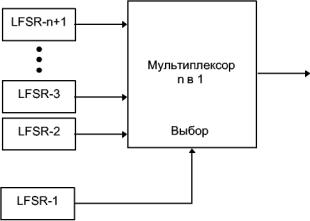
Вместо выбора между двумя LFSR в этой схеме выбирается один из n LFSR, где n является степенью 2. Всего используется n + 1 LFSR (рис. 1). Тактовая частота LFSR-1 должна быть в log2 n раз выше, чем у остальных n LFSR.
Рис. 1. Обобщенный генератор Геффе.
Несмотря на то, что эта схема сложнее генератора Геффе, для взлома можно использовать то же корреляционное вскрытие.
7
Описание алгоритма решения задачи
Решение данной задачи можно разбить на следующие
этапы.
На первом этапе задаются входные условия, а именно:
первоначальные состояния для трех регистров сдвига;
примитивные многочлены, на основе которых будут формироваться последовательности LFSR;
необходимая длина генерируемой последовательности;
список возможных используемых примитивных многочленов.
На следующем этапе рассчитываются линейная сложность и период генерируемой последовательности. Сложность рассчитывается по линейной формуле
(n1 + 1)n2 + n1n3.
Для нахождения периода генерируемой последовательности, рассчитываются периоды трех последовательностей LFSR, а потом находится их наименьшее общее кратное.
На третьем этапе реализуется сам алгоритм Геффе. Генерируются выходные биты следующего состояния LFSRпоследовательностей. Для этого согласно выбранным примитивным многочленам складываются биты текущего состояния LFSR, получившийся результат записывается старшим битом, а младший бит является результатом генерации нового состояния для данной LFSR. Полученные результаты трех LFSR подставляются в формулу
b = (a1 ^ a2) XOR ((¬a1) ^ a3),
8
