3.4. Теплопроводность твердых тел

Все твердые тела способны проводить теплоту. В изотропном твердом теле распространение тепла описывается законом Фурье.

, (3.55)

где Q – плотность теплового потока: тепловой поток через единичное сечение; - градиент температуры вдоль нормали n к изотермической поверхности; – коэффициент теплопроводности [Вт/(м·к)].

Знак минус означает, что теплота течет в направлении, противоположном градиенту температуры, т.е. от горячей области к холодной.

Для анизотропных тел направление теплового потока, в общем случае, не совпадает с направлением n и уравнение (3.54) принимает форму

;;. (3.56)

где ,и - коэффициенты теплопроводности в направлении главных осей кристалла.

В общем случае в твердых телах существуют два механизма теплопроводности: перенос тепла свободными электронами и упругуми колебаниями решетки.

Решеточная теплопроводность обусловлена передачей тепла за счент взаимодействия нормальных колебаний кристаллической решетки.

В реальных кристаллах при не слишком низких температурах колебания атомов носят ангармонический характер. Проявление ангармоничности приводит к тому, что норманальные колебания решетки утрачивают независимый характер и при встречах взаимодействуют друг с другом, обмениваясь энергией и меняя направление своего распространения. Именно вследствие протекания таких процессов взаимодействия упругих волн становится возможной передача энергии от колебаний одной частоты к колебаниям другой частоты и установление в кристалле теплового равновесия.

Описание процесса рассеяния нормальных колебаний друг на друге удобно вести, рассматривая термически возбужденный кристалл как объем, заполненный фононами. В гармоническом приближении, в котором нармальные колебания решетки являются независимыми, фононы образуют идеальный газ (газ невзаимодействующих фононов). Переход к ангармоническим колебаниям эквивалентен введению взаимодействия между фононами, в результате которого могут происходить процессы расщепления фонона на два и более и образование одного фонона из двух. Такие процессы принято назвать фонон-фононным рассеянием. Вероятность их протекания, как и вероятность протекания любых процессов рассеяния, характеризуют эффективным сечением рассеяния σ_Ф. Рассеяние фонона фононом может произойти лишь в том случае, если они сближаются на расстояние, при котором их эффективные сечения начинают перекрываться. Так как рассеяние появляется в результате ангармоничности колебаний атомов, количественной мерой которой является коэффициент ангармоничности g, то естественно положить радиус эффективного сечения фонона пропорциональным g, а σ_Ф ~ g².

Зная эффективное сечение рассеяния σ_Ф, можно вычислить длину свободного пробега λ_Ф фонона, т.е. то среднее расстояние, которое они проходят между двумя проследовательными актами рассеяния. Расчет показывает, что

, (3.57)

где n_Ф – концентрация фононов.

В кинетической теории газов показывается, что коэффициент теплопровожности газов равен

, (3.58)

где λ – длина свободного пробега молекул газа, υ – скорость их теплового движения, с_V – теплоемкость единицы объема газа.

Применим эту формулу к фононному газу, подставив в нее с_V - теплоемкость единицы объема кристалла (фононного газа), λ=λ_Ф – длину свободного пробега фононов и сместо υ – скорость звука (скорость фононов). Тогда получим слудующее выражение для коэффициента теплопроводности решетки:

, (3.59)

Подставив сюда λ_Ф из (3.56), найдем

. (3.60)

В области высоких температур, согласно (3.32), n_Ф~T, поэтому

. (3.61)

Так как в этой области с_V практически не зависит от Т, то коэффициент теплопроводности решетки должен быть обратно пропорциональным абсолютной температуре, что качественно согласуется с опытом.

При температурах ниже дебаевской концентрация фононов резко уменьшается при понижении Т, вследствии чего их длина свободного пробега резко возрастает и при достигает величины, сравнимой с размером кристалла. Поскольку стенки кристалла обычно плохо отроажают фононы, дальнейшее понижение температуры не приводит к увеличению λ_ф, так как последняя определяется просто рпзмерами кристалла. Температурная зависимость теплопроводности решетки в этом диапазоне температур определяется зависимостью от Т теплоемкости кристалла с_V. Так как в области низких температур с_V~T³, то _реш должна быть пропорциональна Т³:

(3.61)

Этот вывод подтверждается рис. 3.12, на котором показана зависимость теплопроводности искусственного сапфира от температуры.

По мере увеличения температуры растет концентрация фононов n_ф, что само по себе должно приводить к росту _реш. Однако повышение n_ф сопровождается увеличением интенсивности фонон-фононного рассеяния и уменьшения длины свободного пробега λ_ф фононов, что должно приводить к падению _реш. При невысоком n_ф превалирующее значение имеет первый фактор и _реш, пройдя через максимум, падает с ростом Т. В области высоких температур это падение происходит примерно обратно пропорционально Т.

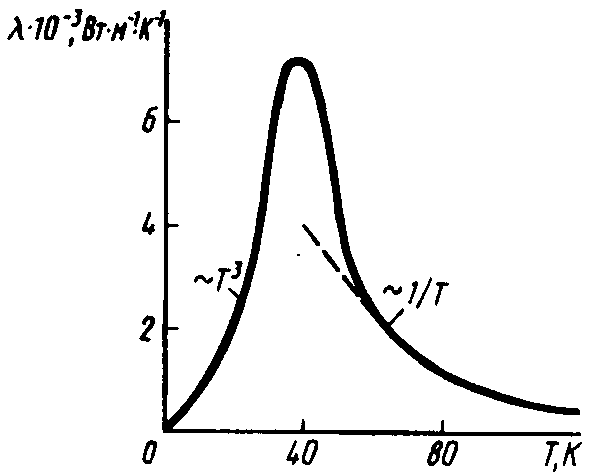
Рис. 3.12. Зависимость теплопроводности сапфира от температуры

Однако теория пока не в состоянии предсказать не только точное значение, но даеж порядок теплопроводности решетки _реш.

Теплопроводность металлов. В металлах перенос теплоты осуществляется не только фононами, но и свободными электронами. Поэтому теплопроводность металлов в общем случае складывается из теплопроводности решетки _реш (теплопроводности, обусловленной фононами) и теплопроводности _е обусловленной свободными электронами

Теплопроводность электронного газа х можно определить, воспользовавшись. Подставив в эту формулу теплоемкость электронного газа (3.58) с_е, скорость электронов υ_F и длину свободного пробега λ_е, получим

. (3.63)

Подставляя сюда из (3.40) найдем

. (3.64)

Определим качественно характер температурной зависимостм чистых металлов.

Область высоких температур. Из всех величин, входящих в правую часть (3.64), от температуры зависит практически только . Для чистых металлов при не слишком низких температурах ,определяется рассеянием электронов на фононах и при прочих одинаковых условиях обратно пропорциональна концентрации фононов n_ф . В области высоких температура, согласно (3.32),n_ф~T. Подставляя это в (3.64) получим

. (3.65)

Таким образом, в области высоких температур теплопроводность чистых металлов не должна зависеть от температуры, что подтверждается экспериментально.

Область низких температур. В этой области, согласно (3.31), концентрация фононов n_ф~T³, поэтому

Подставляя это в (3.64), получим

. (3.66)

Следовательно, в области низких температур, где выполняется закон Дебая, теплопроводность металлов должна быть обратно пропорциональна квадрату абсолютной температуры.

Область очень низких температур. Вблизи абсолютного нуля концентрация фононов в металле становится настолько небольшой, что для процессов рассеяния электронов основное значение приобретают примесные атомы, которые всегда содержатся в металле, сколько бы чистым он ни был. В этом случае длина свободного пробега электронов (N_П – концентрация примесных атомов) перерастает зависеть от температуры и теплопроводность металла, согласно (3.64), оказывается пропорциональной Т.

. (3.67)

Оценим относительную долю, приходящуюся на решеточную теплопроводность металла. Для этого возьмем отношение (3.59) к (3.63):

.

Для чистых металлов,м/с,м,м/с,м. Тогда.

Следовательно, теплопроводность типичных чистых металлов почти полностью определяется теплопроводностью их электронного газа; на долю решеточной проводимости приходится всего лишь несколько процентов.

В металлических сплавах преобладающим механизмом рассеяния электронов является рассеяние на примесных атомах. Длина свободного пробега электронов λ, обусловленная этим рассеянием, обратно пропорциональна концентрации примеси N_П может быть сравнима с длиной свободного пробега фононов . Вклад в теплопроводность электронов в этом случае может по порядку величины быть таким же, как и вклад фононов, т.е.. Исследования показали, что, например, теплопроводность константана (сплава на основе меди и никеля) значительно ниже чем у чистых меди и никеля. Это свидетельствует о том, что за рассеяние электронов в константане ответственны главным образом искажения решетки, вызванные примесными атомами.