Изображение структуры математических моделей

С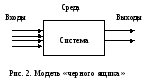труктурную модель системы называют еще структурной схемой или диаграммой связей. Структурные схемы не относятся к обязательным элементам моделирования, однако их свойства позволяют их применять для реализации достаточно абстрактных моделей. Простейшей структурной схемой является модель «черного ящика» (Рис. 1), когда внутреннее устройство системы не представляет интереса, но важно описать ее реакцию на внешние воздействия.

Метод графов

Для отображения структуры модели часто используется метод графов. Граф – это система линий, соединяющих заданные точки. В транспортной системе – это дороги, соединяющие населенные пункты, в электротехнике – проводники, соединяющие различные детали, в химии – взаимосвязи между реагентами. Линии графа, соединяющие заданные точки, называют ветвями. Ветви соединяют вершины графа. Графы, имеющие принципиально одно и тоже строение, называются изоморфными. Если ветви графа пересекаются только в вершинах, такой граф называется плоским.

Путь графа – непрерывная последовательность ветвей в каком-либо одном направлении, в котором ни одна из вершин не встречается более одного раза. Если путь замкнут, то есть начинается и заканчивается в одной и той же вершине, то это называется циклом, а соответствующий граф – циклическим. Граф называется связным, если каждую его вершину можно соединить с любой другой вершиной некоторым путем. Например, граф любой химической реакции является связным. Если же в системе рассматривается несколько независимых реакций, то они образуют несвязный граф.

Каждой ветви графа можно придать определенное численное значение. Например, в кинетике химических реакций каждая стрелка кинетической схемы характеризуется константой скорости данного превращения. Граф, на котором указано направление каждой его ветви, называется ориентированным или направленным. Ветви в ориентированных графах называются также дугами, а в неориентированных графах – ребрами. Граф, в котором имеются как ориентированные, так и неориентированные ветви, называется смешанным.

В любом графе можно выбрать одну из вершин и считать ее базовой. Тогда базовым деревом называется совокупность всех ветвей, проходящих через все вершины графа и направленных к базе. Ветви базового дерева не образуют циклов. Сумма величин всех базовых деревьев, направленных к данной базе, называется базовым определителем графа. Решение графа, например нахождение уравнения скорости какого-либо многоступенчатого процесса, сводится к нахождению всех базовых определителей. Для этого используются следующие свойства графа:

1. Величина пути графа равна произведению величин всех ветвей этого пути. Так, в случае графа

путь (A → D) = abc, . a, b, c – количественные характеристики соответствующих направлений.

2. Параллельные и однонаправленные ветви графа складываются. Таким образом, можно уменьшить число деревьев графа.

3. Ветви, направленные к одной базе, перемножаются:

4. При наличии симметрии можно сливать соответствующие ветви графа.

Метод графов позволяет достаточно легко перейти от графического отображения модели к аналитической ее форме. Рассмотрим, например, обратимое связывание веществА и Б с компонентом почвенного поглощающего комплекса П по следующей схеме:

гдеk₁, k₂, k₃, k₄, k₅, k₆, k₇, k₈ – константы скорости соответствующих реакций. Получить выражения, показывающие соотношение величин А, Б, ПА, ПБ и ПАБ в процессе их взаимодействия представляет собой трудную задачу. Попробуем методом графов определить содержание всех состояний поглощающего комплекса – П, ПА, ПБ и ПАБ при известных концентрациях А и Б в состоянии динамического равновесия. Представим систему (3) в виде графа:

Содержание отдельных форм П_i определяется по формуле

Пi = П0	Di		(4)
	n ∑ i = 1	Di

где П₀ – начальное количество компонента П в системе, D_i – базовый определитель отдельных состояний П.

Проведем построение всех возможных деревьев или путей ведущих к выделенным базам, не образующих циклов. Например, для свободной формы П можно выделить следующие деревья:

Выпишем значения базовых определителей для всех реагентов:

D_П = k₇Ak₆k₂ + k₅Бk₈k₄ + k₈k₄k₂ + k₆k₂k₄

D_ПА = k₃Бk₈k₆ + k₈k₄k₁A + k₄k₁Ak₆+ k₇Ak₆k₁А

D_ПБ = k₁Ak₅Бk₈ + k₆k₂k₃Б + k₅Бk₈k₃Б + k₂k₃Бk₈

D_ПАБ = k₄k₁Ak₅Б + k₂k₃Бk₇A + k₃Бk₇Ak₅Б + k₁Ak₅Бk₇A

Тогда содержание свободной формы П и его комплексов ПА, ПБ и ПАБ в соответствии с формулой (4) определяется следующим образом:

П =	П0DП
	DП + DПА DПБ + DПБ

ПА =	П0DПА
	DП + DПА DПБ + DПБ

ПБ =	П0DПБ
	DП + DПА DПБ + DПБ
ПАБ =	П0DПАБ
	DП + DПА DПБ + DПБ