
4_terehina-li-fik / posobie
.PDF
pRAWOSTORONNIJ PREDEL: |
|
|
|
|
|
|
|
|
|
|
|
|||
lim arctg |
1 |
= arctg |
1 |
|
|
= arctg |
1 |
|
= arctg(+ |
1 |
) = + |
|
: |
|
x ; 2 |
2 + 0 |
; 2 |
+0 |
2 |
||||||||||
x!2+0 |
|
|
|
|
|
|||||||||
kAK WIDIM, \TI PREDELY NE RAWNY MEVDU SOBOJ.
cos x x :
nAJDEM PREDELY \TOJ FUNKCII SLEWA I SPRAWA OT TO^KI x = 0: lEWOSTORONNIJ PREDEL:
|
|
|
|
|
lim |
Sos x |
= cos(;0) |
= cos 0 |
= |
1 |
|
|
= |
;1 |
: |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
;0 |
|
|
|
|
|||||||||||||||||
|
|
|
|
x!;0 |
|
x |
|
|
;0 |
|
|
;0 |
|
|
|
|
|
|
|
|||||||||||
pRAWOSTORONNIJ PREDEL: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
lim |
Sos x = cos(+0) |
= cos 0 |
= |
1 |
|
|
= + |
1 |
: |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
x!+0 |
|
x |
|
|
+0 |
|
|
+0 |
|
+0 |
|
|
|
|
|
|
|
|||||||||
kAK WIDIM, \TI PREDELY NE RAWNY MEVDU SOBOJ. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3: y = |
x2 + 1 |
|
nAJDEM PREDELY FUNKCII PRI x ! ;1 I x ! +1 |
|||||||||||||||||||||||||||
|
2x |
|
|
|
||||||||||||||||||||||||||
|
|
p |
|
|
|
|
p |
|
= |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
lim |
x2 + 1 |
= |
lim |
x2 |
lim |
|
j x j = |
lim |
|
|
x |
= |
1 |
: |
|||||||||||||||
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x!+1 |
|
|
|
|
|
|
|
x!+1 2x |
|
x!+1 |
2x |
|
|
|
x!+1 2x 2 |
|
|||||||||||||
|
lim p |
|
= |
|
|
px2 = |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x2 + 1 |
|
lim |
|
lim |
j x j |
= |
|
|
lim |
|
;x |
= |
; |
1: |
|||||||||||||||
|
x!;1 |
|
|
2x |
|
|
|
x!;1 |
2x |
x!;1 |
2x |
|
x!;1 |
2x |
|
2 |
||||||||||||||
1.4.2. pONQTIE NEPRERYWNOSTI FUNKCII |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
o P R E D E L E N I E |
|
1. fUNKCIQ y = f(x) NAZYWAETSQ NEPRERYWNOJ |
||||||||||||||||||||||||||||
W TO^KE x0 ESLI WYPOLNQ@TSQ TRI USLOWIQ:
1) FUNKCIQ OPREDELENA W \TOJ TO^KE, T.E. SU]ESTWUET ZNA^ENIE FUNKCII
WTO^KE x0 RAWNOE f(x0)
2)ODNOSTORONNIE PREDELY FUNKCII W TO^KE SU]ESTWU@T
lim |
f(x) = A |
lim f(x) = B |
x!x0;0 |
|
x!x0+0 |
3) ODNOSTORONNIE PREDELY RAWNY MEVDU SOBOJ I RAWNY ZNA^ENI@ FUNK- CII W TO^KE
lim f(x) = lim f(x) = f(x0).
x!x0;0 x!x0+0
43

2. fUNKCIQ y = f(x) NAZYWAETSQ NEPRERYWNOJ W TO^KE x0 ESLI SU]ESTWUET PREDEL FUNKCII W TO^KE x0 I \TOT PREDEL RAWEN ZNA^ENI@ FUKCII W \TOJ TO^KE
lim f(x) = f(x0) .
x!x0
w \TOM OPREDELENII PODRAZUMEWAETSQ, ^TO FUNKCIQ OPREDELENA W TO^KE x0 A TAKVE SU]ESTWOWANIE I RAWENSTWO ODNOSTORONNIH PREDELOW EDINO-
MU PREDELU lim f(x):
x!x0
pREOBRAZUEM \TO OPREDELENIE SLEDU@]IM OBRAZOM
lim |
f(x) |
; |
f(x0) = 0 |
) |
lim |
f(x) |
; |
f(x0) |
g |
= 0: |
(x;x0)!0 |
|
|
(x;x0)!0f |
|
|
|
||||
oBOZNA^IM |
x ; x0 = x ; PRIRA]ENIE ARGUMENTA |
|
|
|||||||
f(x) ; f(x0) = f(x) ; PRIRA]ENIE FUNKCII: |
|
|||||||||
tOGDA MOVNO SFORMULIROWATX E]E ODNO OPREDELENIE NEPRERYWNOSTI FUNKCII W TO^KE NA QZYKE PRIRA]ENIJ.
3. fUNKCIQ y = f(x) NAZYWAETSQ NEPRERYWNOJ W TO^KE x0, ESLI BESKONE^NO MALOMU PRIRA]ENI@ ARGUMENTA SOOTWET- STWUET BESKONE^NO MALOE PRIRA]ENIE FUNKCII
lim f(x) = 0:
x!0
1.4.3. kLASSIFIKACIQ TO^EK RAZRYWA
eSLI W TO^KE x0 NARU[AETSQ KAKOE-LIBO USLOWIE NEPRERYWNOSTI FUNK- CII, TO TO^KA x0 NAZYWAETSQ TO^KOJ RAZRYWA FUNKCII.
u S T R A N I M Y J R A Z R Y W. tO^KA x0 NAZYWAETSQ TO^KOJ USTRANI- MOGO RAZRYWA FUNKCII y = f(x) ESLI FUNKCIQ W TO^KE NEOPREDELENA, NO ODNOSTORONNIE PREDELY SU]ESTWU@T I RAWNY MEVDU SOBOJ
(rIS. 1.3) |
|
|
lim |
f(x) = |
lim f(x) = A: |
x!x0;0 |
|
x!x0+0 |
44 |
|
|
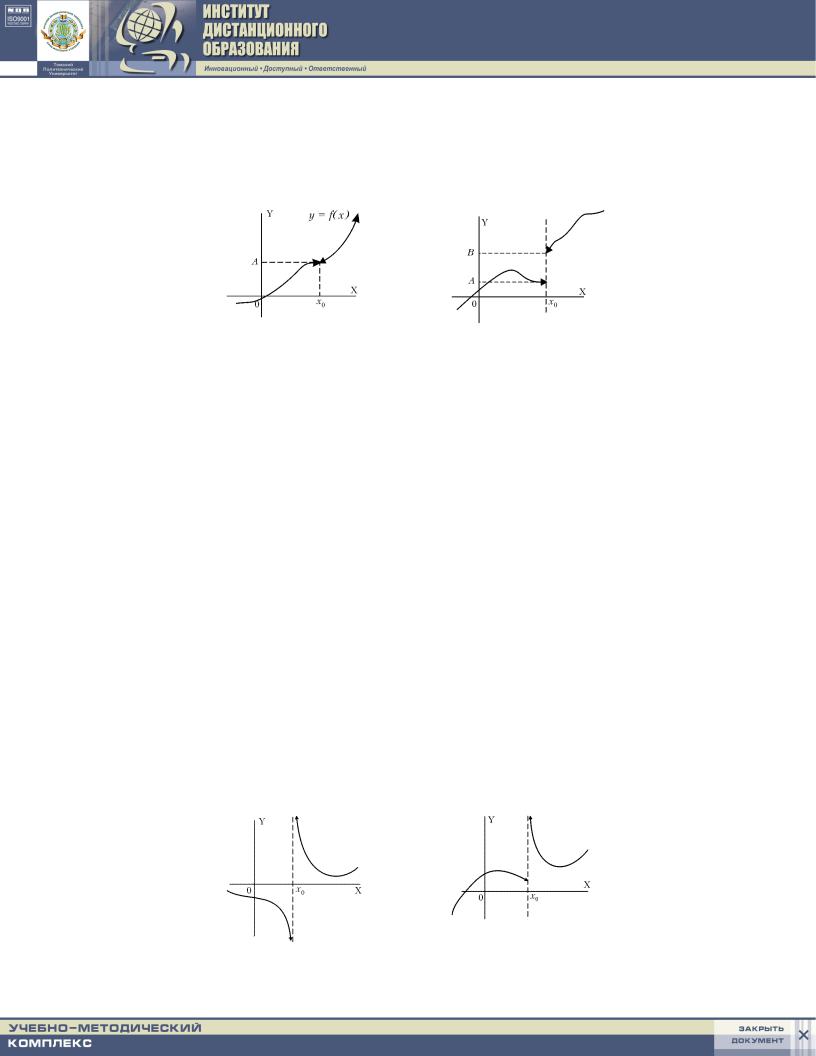
tAKOJ RAZRYW MOVNO USTRANITX, DOOPREDELIW FUNKCI@ W TO^KE RAZRYWA x0 ZNA^ENIEM EE PREDELA A, TOGDA FUNKCIQ ZAPI[ETSQ SISTEMOJ
y = 8 f(x) |
x 6=x0 |
|
< |
A |
x = x0: |
: |
|
|
rIS. 1.3. |
rIS. 1.4. |
n E U S T R A N I M Y J R A Z R Y W I - GO |
R O D A. tO^KA x0 NAZYWA- |
ETSQ TO^KOJ NEUSTRANIMOGO RAZRYWA I- GO RODA (TO^KOJ KONE^NOGO SKA^KA FUNKCII) FUNKCII y = f(x) ESLI ODNOSTORONNIE PREDELY SU]ESTWU@T, NO NE RAWNY MEVDU SOBOJ
lim f(x) 6= lim f(x):
x!x0;0 x!x0+0
pRI \TOM W SAMOJ TO^KE x0 FUNKCIQ MOVET BYTX I NE OPREDELENA. sKA^OK FUNKCII RAWEN ABSOL@TNOJ WELI^INE RAZNOSTI ODNOSTORONNIH PREDELOW
lim |
f(x) |
lim |
f(x) |
j |
. (rIS.1.4 ) |
j x!x0;0 |
|
; x!x0+0 |
|
|
II - GO R O D A. tO^KA x0 NAZYWAETSQ TO^KOJ NEUSTRANIMOGO RAZRYWA II- GO RODA FUNKCII y = f(x) ESLI HOTQ BY ODIN IZ ODNOSTORONNIH PREDELOW NE SU]ESTWUET ILI RAWEN BESKONE^NOSTI
lim |
f(x) = |
1 |
|
lim f(x) = |
1 |
: |
x!x0;0 |
|
|
x!x0+0 |
|
w SLU^AQH, KOGDA ODNOSTORONNIE PREDELY RAWNY BESKONE^OSTI, RAZRYW II- GO RODA NAZYWA@T BESKONE^NYM RAZRYWOM, A TO^KU x0 {TO^KOJ BES- KONE^NOGO SKA^KA FUNKCII (RIS. 1.5, 1.6).
rIS. 1.5. |
rIS. 1.6. |
45

1.4.4. iSSLEDOWANIE FUNKCIJ NA NEPRERYWNOSTX
iSSLEDOWANIE NA NEPRERYWNOSTX SOSTOIT W WYQWLENII TO^EK RAZRYWA I OPREDELENII IH HARAKTERA (T.E. OPREDELENII TIPA RAZRYWA).
1: y = x2 ; 4: x ; 2
dANNAQ FUNKCIQ OPREDELENA NA WSEJ ^ISLOWOJ OSI ZA ISKL@^ENIEM TO^KI x = 2: w \TOJ TO^KE NARU[AETSQ PERWOE USLOWIE OPREDELENIQ 1. NEPRERYWNOSTI FUNKCII, TAK KAK ZNA^ENIE FUNKCII W TO^KE x = 2
PREDSTAWLQET SOBOJ NEOPREDELENNOSTX WIDA ( |
0 |
). tAKIM OBRAZOM, TO^KA |
|
|
|||
|
0 |
|
|
x = 2 |
QWLQETSQ TO^KOJ RAZRYWA FUNKCII. |
||
oPREDELIM TIP RAZRYWA. dLQ \TOGO NAHODIM ODNOSTORONNIE PREDELY W TO^KE x = 2:
lim |
x2 ; 4 |
= |
lim |
(x ; 2)(x + 2) |
= |
lim |
(x + 2)=2 |
|
0 + 2=4: |
x!2 0 |
x ; 2 |
|
x!2 0 |
x ; 2 |
|
x!2 0 |
|
|
oDNOSTORONNIE PREDELY RAWNY MEVDU SOBOJ, TAK KAK POSLE SOKRA]E- NIQ WYRAVENIQ W OSTAW[EMSQ UVE NE SKAZYWAETSQ NALI^IE 0 W ZNAMENATELE.
tAKIM OBRAZOM, MY IMEEM DELO S USTRANIMYM RAZRYWOM FUNKCII. ~TO- BY USTRANITX RAZRYW, POLOVIM ZNA^ENIE FUNKCII W TO^KE x = 2 RAW- NYM ZNA^ENI@ ODNOSTORONNIH PREDELOW, T.E. 4.
iTAK, |
8 x2 |
; 4 |
|
x |
6 |
= 2 |
|
y = > x |
; |
2 |
|
|
|
||
|
< |
|
|
x = 2: |
|||
|
> 4 |
|
|
|
|||
zAPISANNAQ TAKIM OBRAZOM FUNKCIQ UVE QWLQETSQ NEPRERYWNOJ
: .
2: y = e3x ; 1:
2x
dANNAQ FUNKCIQ OPREDELENA NA WSEJ ^ISLOWOJ OSI ZA ISKL@^ENIEM TO^KI x = 0: w \TOJ TO^KE NARU[AETSQ PERWOE USLOWIE OPREDELENIQ 1. NEPRERYWNOSTI FUNKCII, TAK KAK ZNA^ENIE FUNKCII W TO^KE x = 0 PREDSTAWLQET SOBOJ NEOPREDELENNOSTX WIDA tAKIM OBRAZOM, TO^KA x = 0 QWLQETSQ TO^KOJ RAZRYWA FUNKCII.
46

oPREDELIM TIP RAZRYWA. dLQ \TOGO NAHODIM ODNOSTORONNIE PREDELY W TO^KE x = 0: pRAWOSTORONNIJ PREDEL
lim |
e3x ; 1 |
= lim |
3x |
= |
3 |
(+0) |
= |
3 |
: |
x!+0 |
2x |
x!+0 |
2x |
|
2 |
(+0) |
|
2 |
|
pRI NAHOVDENII PREDELA MY WOSPOLXZOWALISX TABLICEJ \KWIWALENTNYH BESKONE^NO MALYH WELI^IN. aNALOGI^NO NAHODIM LEWOSTORONNIJ PREDEL
lim |
e3x ; 1 |
= lim |
3x |
= |
3 (;0) |
= |
3 |
: |
x!;0 |
2x |
x!;0 |
2x |
|
2 (;0) |
|
2 |
|
oDNOSTORONNIE PREDELY RAWNY MEVDU SOBOJ I NE ZAWISQT OT TOGO, S KA- KOJ STORONY K TO^KE x = 0 MY PODHODIM.
tAKIM OBRAZOM, MY IMEEM DELO S USTRANIMYM RAZRYWOM FUNKCII. ~TO- BY USTRANITX RAZRYW, POLOVIM ZNA^ENIE FUNKCII W TO^KE x = 0 RAW- NYM ZNA^ENI@ ODNOSTORONNIH PREDELOW, T.E. 3/2.
|
|
8 |
e3x ; 1 |
x |
6 |
= 0 |
||
|
|
2x |
|
|
||||
|
|
< |
|
|
|
|
||
|
iTAK, |
y = > |
|
|
|
|
||
|
|
> 3=2 |
x = 0: |
|||||
|
|
: |
|
|
|
|
||
tAKAQ FUNKCIQ UVE QWLQETSQ NEPRERYWNOJ. |
||||||||
|
3: y = |
2 |
|
|
: |
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|||
|
5 + 4x+3 |
|
|
|
|
|||
|
|
|
|
|
|
|||
w OBLASTX OPREDELENIQ DANNOJ FUNKCII NE WHODIT TO^KA x = ;3 QW- LQ@]AQSQ W SILU \TOGO TO^KOJ RAZRYWA. oPREDELIM HARAKTER RAZRYWA. nAHODIM PREDEL FUNKCII SLEWA OT TO^KI x = ;3:
lim |
2 |
|
|
= |
|
2 |
|
|
|
= |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
1 |
|
|
|
1 |
|
||||
x!;3;0 |
5 + 4x+3 |
|
5+4 |
3 |
; |
0+3 |
|
|
5+4 |
0 |
|
|||
|
|
|
|
|
|
; |
|
|
|
|
; |
|
||
zDESX MY ISPOLXZOWALI SLEDU@]EE: |
|
|
|
|||||||||||
= |
2 |
= |
2 |
= |
2 |
: |
|
|
|
||||
5+4;1 |
5+0 |
5 |
1 |
= ;1 4;1 = |
1 |
! |
+1 |
= |
1 |
= |
1 |
= 0: |
;0 |
4 |
|
41 |
1 |
nAHODIM PREDEL FUNKCII SPRAWA OT TO^KI x = ;3:
47

|
lim |
|
2 |
|
|
= |
|
2 |
|
= |
2 |
|
|
= |
2 |
= |
2 |
|
= 0: |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
5 + 4+1 |
5 + |
1 |
||||||||
x |
!; |
3+0 |
5+4x+3 |
5+4;3+0+3 |
|
|
|
5+4+0 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
iTAK, ODNOSTORONNIE PREDELY SU]ESTWU@T, |
|
|
|
|
||||||||||||||||||
NO NE RAWNY MEVDU SOBOJ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
lim |
y = 2=5 |
= lim |
|
y |
= 0: |
|
|
|
|
|
|
|
|
||||||
|
|
x!;3;0 |
|
|
|
|
6 x!;3+0 |
|
|
|
|
|
|
|
|
|
|
|||||
rIS. 1.7.
wYWOD : W TO^KE x = ;3 FUNKCIQ TERPIT NEUSTRANIMYJ RAZRYW
I - GO RODA. sKA^OK FUNKCII RAWEN RAZNOSTI ODNOSTORONNIH PREDELOW,
T.E. 2/5.
dOPOLNITELXNO MOVNO WY^ISLITX PREDEL \TOJ FUNKCII PRI x ! 1
|
|
lim |
|
|
|
2 |
|
|
|
|
|
= |
|
|
|
|
2 |
|
|
|
|
= |
2 |
= |
2 |
|
= 2=6 = 1=3: |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
5 + 40 |
|
|
|||||||||||
|
|
x |
!1 5 + 4x+3 |
|
5 + 41 |
|
|
|
5 + 1 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
nA RISUNKE 1.7 PREDSTAWLEN \SKIZ GRAFIKA DANNOJ FUNKCII. |
||||||||||||||||||||||||||||||
|
|
|
|
3x2 |
|
|
|
|
|
|
x < 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4: y = 8 p |
|
|
0 x < 1 |
|
|
|
|
|
|
||||||||||||||||||||
|
1 x2 |
|
rIS. 1.8. |
|
||||||||||||||||||||||||||
|
|
> |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
< |
|
|
|
|
|
|
|
|
|
x 1: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
> x ; 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
fUNKCIQ :OPREDELENA NA WSEJ ^ISLOWOJ OSI, ODNAKO, DLQ RAZNYH PROME- |
||||||||||||||||||||||||||||||
VUTKOW FUNKCIQ ZADANA RAZLI^NYMI URAWNENIQMI, PRI^EM W KAVDOM |
||||||||||||||||||||||||||||||
IZ PROMEVUTKOW FUNKCIQ QWLQETSQ NEPRERYWNOJ, PO\TOMU RAZRYWY MO- |
||||||||||||||||||||||||||||||
GUT BYTX TOLXKO NA STYKE PROMEVUTKOW. |
|
|
|
|
||||||||||||||||||||||||||
iTAK, RAZRYW WOZMOVEN W TO^KAH x1 = 0 I x2 = 1: |
|
|||||||||||||||||||||||||||||
rASSMOTRIM PERWU@ TO^KU. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
1) x1 = 0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
nAJDEM ODNOSTORONNIE PREDELY |
|
|
|
|
|
|
||||||||||||||||||||||||
|
lim |
y = |
lim (3x2) = (3 |
|
02) = 0 |
|
|
|
|
|
||||||||||||||||||||
|
x!;0 |
|
|
x!;0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
p1 |
|
|
|
x2 |
|
|
|
|
|
|
|
02 |
= 1: |
|
|
|
|
||||||||||
|
lim |
y = lim |
; |
= p1 |
; |
|
|
|
|
|||||||||||||||||||||
|
x!+0 |
|
|
x!+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
iTOG: oDNOSTORONNIE PREDELY SU]ESTWU@T, NO NE RAWNY MEVDU SO- BOJ. pO\TOMU W TO^KE x = 0 FUNKCIQ TERPIT RAZRYW I- GO RODA. sKA^OK RAWEN 1 ; 0 = 1:
48

rASSMOTRIM WTORU@ TO^KU. 2) x2 = 1:
nAJDEM ODNOSTORONNIE PREDELY
|
|
lim |
y = |
lim (p1 |
; |
x2) = |
|
|||
|
|
x!1; |
0 |
|
x!1;0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= p1 ; 12 = 0 |
|
|
|
|
|
|||
rIS |
. 1.9. |
lim |
y = |
lim (x |
; |
1) = 1 |
; |
1 = 0: |
||
x!1+0 |
|
x!1+0 |
|
|
|
|||||
|
|
nAJDEM |
ZNA^ENIE |
FUNKCII |
W TO^KE x = |
|||||
|
|
1 : |
|
y(1) = x ; 1 = 1 ; 1 = 0: |
||||||
iTOG: oDNOSTORONNIE PREDELY SU]ESTWU@T, RAWNY MEVDU SOBOJ I RAWNY ZNA^ENI@ FUNKCII W TO^KE. pO\TOMU, SOGLASNO OPREDELENIQ 1, W TO^KE x = 1 FUNKCIQ NEPRERYWNA.
pOSTROIM GRAFIK \TOJ FUNKCII:
1) dLQ x < 0 IMEEM y = 3x2 { \TO LEWAQ WETWX PARABOLY.
2) dLQ 0 x < 1 IMEEM y = p1 ; x2 { \TO ^ASTX OKRUVNOSTI x2 + y2 = 1 RASPOLOVENNAQ W PERWOJ ^ETWERTI.
3) dLQ x 1 IMEEM y = x ; 1 { OTREZOK PRQMOJ LINII.
iZ GRAFIKA WIDNO, ^TO W TO^KE x = 0 FUNKCIQ TERPIT RAZRYW, TAK KAK GRAFIKI PARABOLY I OKRUVNOSTI NE SOSTYKOWALISX, A W TO^KE x = 1 GRAFIK FUNKCII y = p1 ; x2 NEPRERYWNO PEREHODIT W GRAFIK FUNKCII y = x ; 1: (rIS.1.9)
5: y = 1 ; 2jxxj:
w OBLASTX OPREDELENIQ DANNOJ FUNKCII NE WHODIT TO^KA x = 0: w jxxj PRI x = 0 IMEEM NEOPREDELENOSTX WIDA 00! :
kROME TOGO, NEOBHODIMO WSPOMNITX OPREDELENIE MODULQ x:
8 |
;x |
ESLI |
< |
|
|
jxj = > |
0 |
ESLI |
> |
x |
ESLI |
: |
|
|
x < 0 x = 0 x > 0:
49

nAHODIM ODNOSTORONIE PREDELY
xlim0 |
0 1 |
; 2 |
jxj |
1 = xlim0 |
1 ; 2 |
|
;x |
! = 1 ; 2; |
1 |
= 1 ; 1=2 = 1=2: |
|||||||||||||
x |
|
x |
|
||||||||||||||||||||
!; |
@ |
|
|
A |
!; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
0 |
2 jxj1 |
= lim |
|
1 |
|
|
2 x |
|
= 1 |
|
21 |
= 1 |
|
2 = |
|
1: |
|||||
x!+0 |
@; |
|
A |
x!+0 |
; |
|
|
|
|
|
; |
|
|
|
; |
|
; |
|
|||||
oDNOSTORONNIE PREDELY SU]ESTWU@T, NO NE |
|
|
|
|
|
|
|
||||||||||||||||
RAWNY MEVDU SOBOJ. tAKIM OBRAZOM, MY IME- |
|
|
|
|
|
|
|
||||||||||||||||
EM W TO^KE x = 0 NEUSTRANIMYJ RAZRYW I-GO |
|
|
|
|
|
|
|
||||||||||||||||
RODA. sKA^OK FUNKCII W TO^KE RAZRYWA PO |
|
|
|
|
|
|
|
||||||||||||||||
ABSOL@TOJ WELI^INE RAWEN 1=2 |
; |
( |
; |
1) = 3=2: |
|
|
|
rIS. 1.10. |
|||||||||||||||
pOWEDENIE FUNKCII W OKRESTNOSTI TO^KI RAZRYWA POKAZANO NA RISUNKE
1.10.
6: y = xx2+;59:
zNAMENATELX DROBI OBRA]AETSQ W NOLX PRI x = ;3 I x = 3: |TI ZNA- ^ENIQ NE WHODQT W OBLASTX OPREDELENIQ FUNKCII I QWLQ@TSQ TO^KAMI RAZRYWA. oPREDELIM TIP RAZRYWA. dLQ \TOGO NAJDEM ODNOSTORONNIE PREDELY W KAVDOJ TO^KE.
1) x = ;3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
x + 5 |
= |
lim |
|
|
x + 5 |
|
|
|
= |
|
|
|
;3 + 5 |
|
|
|
= |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x!;3;0 x2 ; 9 |
|
x!;3;0 (x + 3)(x ; |
3) |
|
(;3 ; 0 + 3)(;3 ; 3) |
|
|||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
= |
|
|
|
|
= + |
|
0 |
= +1: |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
(;0) |
(;6) |
3 |
|
|
|
|
|
|
|||||||||||
lim |
x + 5 |
= |
lim |
|
x + 5 |
|
|
|
= |
|
|
|
;3 + 5 |
|
|
|
= |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x!;3+0 x2 |
; |
9 |
|
x!;3+0 (x + 3)(x |
; |
3) |
|
( |
; |
3 + 0 + 3)( |
; |
3 |
; |
3) |
|
||||||||||
|
|
|
|
|
2 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
= |
|
|
= ; |
|
0 |
= ;1: |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
(+0) |
(;6) |
3 |
|
|
|
|
|
|
|||||||||||
oBA ODNOSTORONNIH PREDELA RAWNY BESKONE^NOSTI, ZNA^IT FUKCIQ W |
|||||||||||||||||||||||||
TO^KE x = |
;3 TERPIT NEUSTRANIMYJ RAZRYW II-GO RODA, ILI BESKONE^- |
||||||||||||||||||||||||
NYJ RAZRYW. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50

2) x = 3 x + 5 lim 2
x!3;0 x8 ; 9
= (6) (;0)
x + 5 lim 2
x!3+0 x8 ; 9
= (6) (+0)
= |
|
lim |
|
|
x + 5 |
|
||
|
|
|
|
|
||||
|
(x + 3)(x |
; 3) |
||||||
|
x!3;0 |
|||||||
|
4 |
1 |
|
|
|
|
||
= |
|
|
|
|
|
= ;1: |
|
|
3 |
;0 |
|
||||||
= |
|
lim |
|
|
x + 5 |
|
||
|
(x + 3)(x |
; 3) |
||||||
|
x!3+0 |
|||||||
|
4 |
1 |
|
|
|
|
||
= |
|
|
|
|
= +1: |
|
||
3 |
+0 |
|
||||||
3 + 5 = (3 + 3)(3 ; 0 ; 3) =
3 + 5 = (3 + 3)(3 + 0 ; 3) =
oBA ODNOSTORONNIH PREDELA RAWNY BESKONE^NOSTI, ZNA^IT FUNKCIQ W TO^KE x = 3 TERPIT NEUSTRANIMYJ RAZRYW II-GO RODA, ILI BESKONE^NYJ RAZRYW.
|
|
|
|
|
pREDEL FUNKCII PRI x |
! 1, O^EWIDNO, RA- |
||||||||||||||||||||
|
|
|
|
|
WEN NUL@ |
|
|
|
|
|
|
|
|
|
|
|
x + 5 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
= 0: |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x!1 x2 ; |
9 |
|
|
|
|
|
|||||||||
|
|
|
|
|
pOWEDENIE GRAFIKA W OKRESTNOSTQH TO^EK |
|||||||||||||||||||||
rIS. 1.11. |
|
|
|
|
RAZRYWA POKAZANO NA RISUNKE 1.11. |
|||||||||||||||||||||
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7: y = 2 ; 3 5 + x: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
o^EWIDNO, ^TO FUNKCIQ RAZRYWNA W TO^KE x = ;5: |
|
|
|
|
||||||||||||||||||||||
nAHODIM ODNOSTORONNIE PREDELY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
7 |
! |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
7 |
|
||
|
lim |
2 |
; |
3 5+x |
= 2 |
; |
3 |
5 |
; |
5 |
; |
0 = 2 |
; |
3 |
; |
0 = |
||||||||||
x!;5;0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
= 2 ; 3;1 |
= 2 ; |
1 |
= 2 ; |
|
|
1 |
|
|
|
= 2 |
; 0 = 2: |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
3+1 |
71 |
||||||||||||||||||||||||
|
|
|
|
|
|
7 |
! |
|
|
|
|
|
|
|
|
|
|
7 |
|
|||||||
|
lim |
2 |
; |
3 5+x |
= 2 |
; |
3 |
5 |
; |
5+0 = 2 |
; |
3 |
+0 = |
|||||||||||||
x!;5+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
= 2 ; 3+1 = 2 ; 1 |
= |
;1: |
|
|
|
|
|
|
||||||||||||||
oDIN IZ ODNOSTORONNIH PREDELOW RAWEN |
;1, ZNA^IT W TO^KE x = ;5 |
|||||||||||||||||||||||||
FUNKCIQ IMEET NEUSTRANIMYJ RAZRYW II-GO RODA. |
|
|
|
|
||||||||||||||||||||||
51

dOPOLNITELXNO MOVNO NAJTI PREDEL FUNK- CII PRI x ! 1
|
|
|
|
|
|
|
7 |
! |
|
|
lim |
2 |
; |
35+x |
= |
|
|||||
x!1 |
|
|
|
|
|
|||||
|
7 |
|
= 2 ; 30 = 2 ; 1 = 1: |
|
||||||
= 2 ; 31 |
|
|||||||||
nA RISUNKE 1.12 |
POKAZAN \SKIZ GRAFIKA DAN- |
rIS. 1.12. |
||||||||
NOJ FUNKCII.
1.4.5. sWOJSTWA NEPRERYWNYH FUNKCIJ
1.wSE OSNOWNYE \LEMENTARNYE FUNKCII NEPRERYWNY W OBLASTI IH OPREDELENIQ.
2.sUMMA, RAZNOSTX I PROIZWEDENIE NEPRERYWNYH FUNKCIJ ESTX FUNK- CIQ NEPRERYWNAQ. ~ASTNOE DWUH NEPRERYWNYH FUNKCIJ ESTX NEPRERYW- NAQ FUNKCIQ, ESLI FUNKCIQ, STOQ]AQ W ZNAMENATELE, NE OBRA]AETSQ W NOLX W TO^KE x0:
3.sLOVNAQ FUNKCIQ, SOSTAWLENNAQ IZ NEPRERYWNYH FUNKCIJ, NEPRE- RYWNA.
4.fUNKCIQ NAZYWAETSQ NEPRERYWNOJ W PROMEVUTKE, ESLI ONA NEPRE- RYWNA W KAVDOJ TO^KE \TOGO PROMEVUTKA.
sWOJSTWA FUNKCIJ, NEPRERYWNYH W ZAMKNUTOM PROMEVUTKE
t E O R E M A wEJER[TRASSA. |
fUNKCIQ f(x) NEPRERYWNAQ W ZA- |
|
MKNUTOM PROMEVUTKE [a b] |
DOSTIGAET W \TOM PROMEVUTKE SWOEGO NAI- |
|
BOLX[EGO M I NAIMENX[EGO |
m ZNA^ENIJ. |
|
t.E. SU]ESTWU@T TAKIE TO^KI x1 I x2 |
PROMEVUTKA [a b] ^TO DLQ WSEH |
|
x IZ [a b] WYPOLNQ@TSQ NERAWENSTWA |
|
|
f(x1) f(x) |
f(x2) f(x): |
|
zNA^ENIE f(x1) = M NAZYWAETSQ NAIBOLX[IM ZNA^ENIEM FUNKCII W IN-
TERWALE.
zNA^ENIE f(x2) = m NAZYWAETSQ NAIMENX[IM ZNA^ENIEM FUNKCII W IN-
TERWALE.
52
