4_terehina-li-fik / posobie

gLAWA 1. funkciq i ee predel

1.1.pONQTIE FUNKCII

oSNOWNYE \LEMENTARNYE FUNKCII

pRI IZU^ENII RAZLI^NYH QWLENIJ MY POSTOQNNO STALKIWAEMSQ S PO- STOQNNYMI I PEREMENNYMI WELI^INAMI RAZLI^NOJ PRIRODY. pRIMERA- MI POSTOQNNYH WELI^IN QWLQ@TSQ, NAPRIMER, ^ISLO = 3 14:::, ^ISLO

T.P. k PEREMENNYM WELI^INAM OTNOSQTSQ: WREMQ, SKOROSTX, DAWLENIE, TEMPERATURA, SILA I T.P. iZMENENIE ODNOJ PEREMENNOJ WELI^INY, ^A]E WSEGO, PROISHODIT WSLED ZA IZMENENIEM ODNOJ ILI NESKOLXKIH DRUGIH. w \TOM SLU^AE GOWORQT, ^TO PEREMENNYE SWQZANY MEVDU SOBOJ ILI ZAWISQT DRUG OT DRUGA. mATEMATI^ESKOJ MODELX@ TAKOJ ZAWISIMOSTI QWLQETSQ FUNKCIQ.

o P R E D E L E N I E. eSLI KAVDOMU ZNA^ENI@ PEREMENNOJ x SO- OTWETSTWUET OPREDELENNOE ZNA^ENIE PEREMENNOJ y, TO GOWORQT, ^TO PEREMENNAQ y QWLQETSQ FUNKCIEJ NEZAWISIMOJ PEREMENNOJ x I OBOZNA- ^A@T TAKU@ ZAWISIMOSTX SLEDU@]IM OBRAZOM:

y = y(x) ILI y = f(x):

nEZAWISIMAQ PEREMENNAQ x NAZYWAETSQ ARGUMENTOM FUNKCII y = f(x):

w MATEMATI^ESKOM ANALIZE DLQ ZADANIQ FUNKCII ISPOLXZU@T, W OS- NOWNOM, ANALITI^ESKIJ SPOSOB ZADANIQ FUNKCII, KOGDA DLQ OPISANIQ FUNKCIONALXNOJ ZAWISIMOSTI IMEETSQ ANALITI^ESKOE WYRAVENIE, W KO- TOROM UKAZANY WSE DEJSTWIQ, KOTORYE NUVNO PRODELATX NAD NEZAWISI- MOJ PEREMENNOJ, ^TOBY POLU^ITX ZNA^ENIE FUNKCII.

pRI ANALITI^ESKOM ZADANII FUNKCII RAZLI^A@T FUNKCII, ZADANNYE

\TOM SLU^AE ODNU PEREMENNU@ S^ITA@T ARGUMENTOM, TOGDA DRUGAQ BU- DET FUNKCIEJ. w RQDE SLU^AEW NEQWNAQ FUNKCIQ MOVET BYTX ZAPISANA W QWNOM WIDE, NAPRIMER WYRAVENIE x2 + y2 = 4 NEQWNO OPREDELQET 2

3

FIK. gRAFIK FUNKCII {\TO LINIQ NA PLOSKOSTI. kOORDINATY (x y) KAVDOJ TO^KI \TOJ LINII UDOWLETWORQ@T URAWNENI@ y = f(x): zNAQ ANALITI^ESKOE WYRAVENIE, OPREDELQ@]EE FUNKCI@, MOVNO DLQ KON- KRETNYH ZNA^ENIJ x WY^ISLITX PO ZADANNOJ FORMULE ZNA^ENIE FUNKCII y I POSTROITX EE GRAFIK.

pRI IZU^ENII FUNKCII NEOBHODIMO ZNATX EE OBLASTX OPREDELENIQ.

o P R E D E L E N I E. oBLASTX@ OPREDELENIQ FUNKCII NAZYWAETSQ MNOVESTWO ZNA^ENIJ NEZAWISIMOJ PEREMENNOJ, PRI KOTORYH WYRAVE-

y = x2 ex OPREDELENA DLQ L@BYH ZNA^ENIJ x: bOLX[OE KOLI^ESTWO PRI- MEROW NAHOVDENIQ OBLASTEJ OPREDELENIQ FUNKCIJ PRIWEDENY W GLAWE 3 NASTOQ]EGO POSOBIQ.

rAZLI^A@T FUNKCII: OSNOWNYE \LEMENTARNYE, \LEMENTARNYE, NE\LE- MENTARNYE, PROSTYE, SLOVNYE, ALGEBRAI^ESKIE, NEALGEBRAI^ESKIE.

k OSNOWNYM \LEMENTARNYM FUNKCIQM OTNOSQTSQ SLEDU@]IE 5 TIPOW

4

w MATEMATIKE I EE PRILOVENIQH ^ASTO ISPOLXZU@TSQ GIPERBOLI^ESKIE

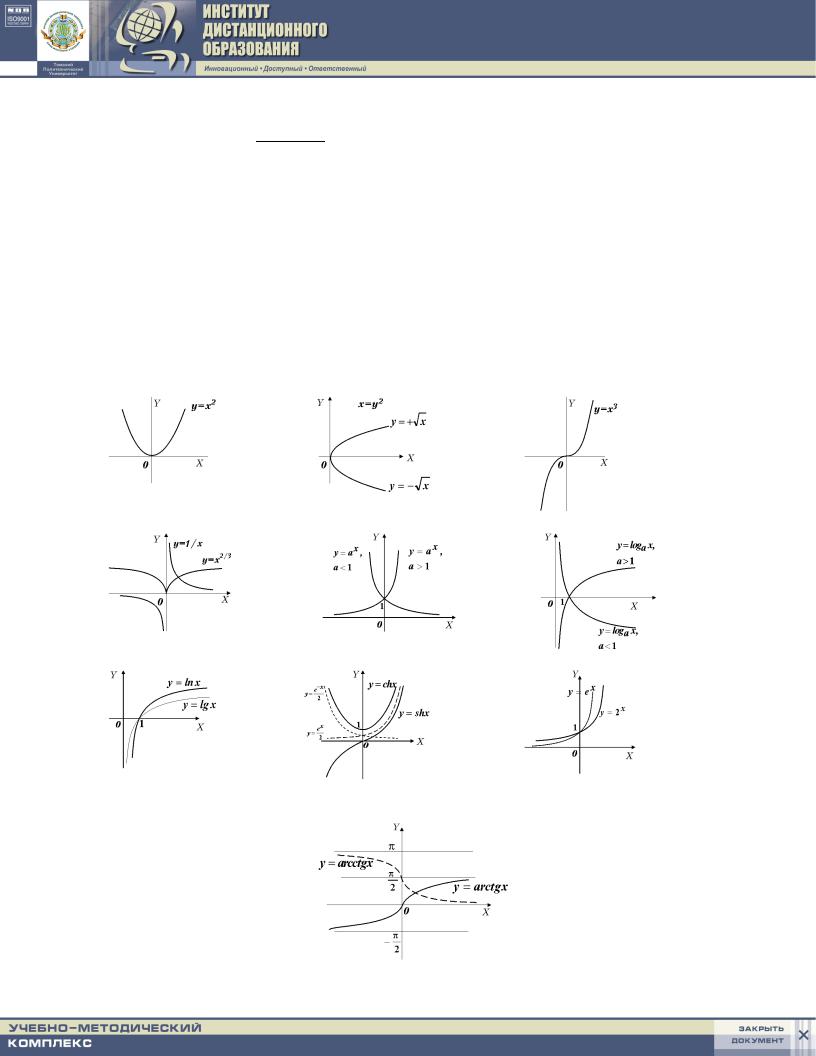
gRAFIKI OSNOWNYH \LEMENTARNYH FUNKCIJ

5

fUNKCIQ NAZYWAETSQ:

\ L E M E N T A R N O J, ESLI ONA PREDSTAWLQETSQ W WIDE KONE^NOGO ANALITI^ESKOGO WYRAVENIQ

N E \ L E M E N T A R N O J, ESLI ONA NE MOVET BYTX PREDSTAWLENA W WIDE KONE^NOGO ANALITI^ESKOGO WYRAVENIQ. s TAKIMI FUNKCIQMI MY WSTRETIMSQ POZVE

P R O S T O J, ESLI ONA SOSTAWLENA IZ OSNOWNYH \LEMENTARNYH S POMO]X@ ARIFMETI^ESKIH OPERACIJ, NAPRIMER

y = 1 ; x2 y = x sin x ; px + tgx 1 + x2

S L O V N O J, ESLI ONA SODERVIT OPERACII NAHOVDENIQ FUNKCII OT FUNKCII, T.E. ARGUMENTOM SLOVNOJ FUNKCII QWLQETSQ TAKVE NEKOTORAQ FUNKCIQ, NAPRIMER

y = (1 ; 3x2)5 y = ln3(cos 3x) y = x + ex2;4x

pRIMEROM SLOVNOJ FUNKCII QWLQETSQ P O K A Z A T E L X N O -

S T E P E N N A Q FUNKCIQ, W KOTOROJ NEZAWISIMAQ PEREMENNAQ WHODIT KAK W OSNOWANIE, TAK I W POKAZATELX STEPENI, NAPRIMER

pRI IZU^ENII POWEDENIQ FUNKCII, NAPRIMER S CELX@ POSTROENIQ EE GRAFIKA, WOZNIKAET NEOBHODIMOSTX ISSLEDOWANIQ FUNKCII WBLIZI TO- ^EK RAZRYWA FUNKCII I NA BESKONE^NOSTI. tAKIE ISSLEDOWANIQ SLEDUET PROWODITX S POMO]X@ P R E D E L O W FUNKCII.

1.2. pREDEL FUNKCII

1.2.1. pONQTIE PREDELA FUNKCII

pONQTIE PREDELA QWLQETSQ ODNIM IZ WAVNEJ[IH PONQTIJ MATEMATI- ^ESKOGO ANALIZA, S NIM TESNO SWQZANY PONQTIQ NEPRERYWNOSTI FUNKCII, PROIZWODNOJ I INTEGRALA.

1. pONQTIE PREDELA FUNKCII PRI x ! x0.

pUSTX ZNA^ENIQ x POSTEPENNO PRIBLIVA@TSQ K TO^KE x0 ( GOWORQT, ^TO

6

x STREMITSQ K x0 I ZAPISYWA@T x ! x0). |TO ZNA^IT, ^TO RAZNOSTX MEVDU ZNA^ENIQMI x I x0 UMENX[AETSQ I STREMITSQ K NUL@, T.E. MOVET STATX MENX[E L@BOGO SKOLX UGODNO MALOGO POLOVITELXNOGO ^IS- LA . tAKIM OBRAZOM, STREMLENIE x K x0 MOVNO OPISATX NERAWENSTWOM j x ; x0 j< :

pUSTX PRI \TOM, SOOTWETSTWU@]IE ZNA^ENIQ FUNKCII y = f(x) NE- OGRANI^ENNO PRIBLIVA@TSQ K NEKOTOROMU ^ISLU A ( GOWORQT, ^TO f(x) STREMITSQ K A I ZAPISYWA@T ! A). pRI \TOM RAZNOSTX MEVDU ZNA^ENIQMI FUNKCII I ^ISLOM A WSE WREMQ UMENX[AETSQ I STREMITSQ K NUL@: [f(x) ; A] ! 0 A ZNA^IT MOVET STATX MENX[E SKOLX UGODNO MALOGO POLOVITELXNOGO ^ISLA ": sTREMLENIE f(x) K A MOVNO OPISATX NERAWENSTWOM j f(x) ; A j< ":

pRIWEDEM STROGOE MATEMATI^ESKOE OPREDELENIE PREDELA FUNKCII PRI x ! x0 NA "QZYKE " ":

o P R E D E L E N I E. ~ISLO A NAZYWAETSQ PREDELOM FUNKCII y = f(x) PRI x ! x0 ESLI DLQ L@BOGO SKOLX UGODNO MALOGO POLOVITELXNOGO ^ISLA " NAJDETSQ TAKOE MALOE POLOVITELXNOE ^ISLO (") ^TO DLQ WSEH ZNA^ENIJ x, UDOWLETWORQ@]IH NERAWENSTWU 0 <j x ; x0 j< BUDET WYPOLNQTXSQ NERAWENSTWO j f(x);A j< : tOT FAKT, ^TO ^ISLO A ESTX PREDEL FUNKCII PRI x ! x0 ZAPISYWAETSQ SIMWOLI^ESKI

lim f(x) = A:

x!x0

nERAWENSTWA 0 <j x ; x0 j< I j f(x) ; A j< " S POMO]X@ KO- TORYH DAETSQ STROGOE MATEMATI^ESKOE OPREDELENIE PREDELA FUNKCII,

OZNA^A@T, ^TO ZNA^ENIQ x PRINADLEVAT INTERWALU

KOTORYJ NAZYWAETSQ " ; OKRESTNOSTX@" TO^KI x0, A ZNA^ENIQ FUNK- CII f(x) PRI \TOM PRINADLEVAT INTERWALU

A ; " < f(x) < A + " ILI f(x) 2 (A ; " A + ")

KOTORYJ NAZYWAETSQ "" ; OKRESTNOSTX@" TO^KI A:

g E O M E T R I ^ E S K A Q ILL@STRACIQ PREDELA FUNKCII POKAZANA NA RIS.1.1.

7

2. pONQTIE PREDELA FUNKCII PRI x ! 1.

pUSTX ZNA^ENIQ ARGUMENTA x NEOGRANI^ENNO UWELI^IWA@TSQ PO ABSO- L@TNOJ WELI^INE (GOWORQT, ^TO x STREMITSQ K BESKONE^NOSTI I ZAPI- SYWA@T x ! 1). |TO OZNA^AET, ^TO ZNA^ENIQ jxj STANOWQTSQ BOLX- [E SKOLX UGODNO BOLX[OGO POLOVITELXNOGO ^ISLA N T.E. j x j> N: pRI \TOM ZNA^ENIQ FUNKCII POSTEPENNO PRIBLIVA@TSQ K ZNA^ENI@

A, T.E. jf(x) ; Aj ! 0 ILI jf(x) ; Aj < ":

o P R E D E L E N I E. ~ISLO A NAZYWAETSQ PREDELOM FUNKCII y = f(x) PRI x ! 1 ESLI DLQ L@BOGO SKOLX UGODNO MALOGO POLOVITELXNOGO ^ISLA " NAJDETSQ TAKOE POLOVITELXNOE ^ISLO N( ) ^TO DLQ WSEH ZNA^ENIJ x,

tOT FAKT, ^TO ^ISLO A ESTX PREDEL FUKCII PRI x ! 1 ZAPISYWAETSQ SIMWOLI^ESKI SLEDU@]IM OBRAZOM:

~ASTNYM SLU^AEM FUNKCII MOVET QWLQTXSQ FUNKCIQ NATURALXNOGO

8

ARGUMENTA, KOGDA ZNA^ENIQ x = 1 2 3 :::n ::: . zNA^ENIQ f(n) TAKOJ FUNKCII OBRAZU@T ^ISLOWU@ POSLEDOWATELXNOSTX fang

NOM an: pREDEL ^ISLOWOJ POSLEDOWATELXNOSTI MOVNO RASSMATRIWATX KAK PREDEL SOOTWETSTWU@]EJ FUNKCII f(n) PRI n ! 1.

1.2.2. bESKONE^NO MALYE I BESKONE^NO BOLX[IE WELI^INY.

eSLI FUNKCIQ f(x) PRI x ! x0 STREMITSQ K NUL@, ILI ESLI PREDEL FUNKCII RAWEN NUL@ PRI x ! x0, TO FUNKCI@ f(x) NAZYWA@T

B E S K O N E ^ N O M A L O J WELI^INOJ W OKRESTNOSTI TO^KI x0: bESKONE^NO MALYE WELI^INY (FUNKCII) OBOZNA^A@T (x) (x) (x): tOGDA TOT FAKT, ^TO f(x) QWLQETSQ BESKONE^NO MALOJ ZAPISYWA@T SIM- WOLI^ESKI WYRAVENIEM

bESKONE^NO MALYE WELI^INY OBLADA@T SLEDU@]IMI SWOJSTWAMI:

1)pRI SLOVENII KONE^NOGO ^ISLA BESKONE^NO MALYH WELI^IN POLU- ^AETSQ BESKONE^NO MALAQ WELI^INA.

2)pRI UMNOVENII BESKONE^NO MALYH WELI^IN POLU^AETSQ BESKONE^- NO MALAQ WELI^INA.

3)pRI UMNOVENII BESKONE^NO MALOJ WELI^INY NA KONSTANTU ILI OGRANI^ENNU@ FUNKCI@ POLU^AETSQ BESKONE^NO MALAQ WELI^INA.

eSLI FUNKCIQ NEOGRANI^ENNO WOZRASTAET PO ABSOL@TNOJ WELI^INE (GO- WORQT, ^TO FUNKCIQ STREMITSQ K BESKONE^NOSTI, T.E. f(x) ! 1) PRI

x ! x0, ILI x ! 1, TO FUNKCI@ f(x) NAZYWA@T B E S K O N E ^ N O B O L X [ O J WELI^INOJ W OKRESTNOSTI TO^KI x0, ILI NA BESKONE^NOSTI. bES-

KONE^NO BOLX[IE WELI^INY (FUNKCII) OBOZNA^A@T A(x) B(x) G(x):

9

tOGDA TOT FAKT, ^TO f(x) QWLQETSQ BESKONE^NO BOLX[OJ ZAPISYWA@T SIMWOLI^ESKI WYRAVENIEM

;1 TO f(x) < ;M: :

bESKONE^NO BOLX[IE WELI^INY OBLADA@T SLEDU@]IMI SWOJSTWAMI

1)pRI SLOVENII BESKONE^NO BOLX[IH WELI^IN POLU^AETSQ WELI^INA BESKONE^NO BOLX[AQ.

2)pRI UMNOVENII BESKONE^NO BOLX[IH WELI^IN POLU^AETSQ WELI^I- NA BESKONE^NO BOLX[AQ.

3)pRI UMNOVENII BESKONE^NO BOLX[OJ WELI^INY NA KONSTANTU (NE RAWNU@ NUL@) ILI OGRANI^ENNU@ FUNKCI@ (NE STREMQ]U@SQ K NUL@) POLU^AETSQ BESKONE^NO BOLX[AQ WELI^INA.

sWQZX BESKONE^NO MALOJ I BESKONE^NO BOLX[OJ WELI^IN. wELI^INA,

OBRATNAQ BESKONE^NO MALOJ, ESTX WELI^INA BESKONE^NO BOLX[AQ. wELI^INA, OBRATNAQ BESKONE^NO BOLX[OJ, ESTX WELI^INA BESKONE^NO MA- LAQ.

[U@ WELI^INU PREDSTAWLQET SOBOJ NEOPREDELENNOSTX WIDA (0 1) :

10

pRI WY^ISLENII PREDELOW NAM PONADOBQTSQ PRAWILA OBRA]ENIQ S PREDELAMI, NEKOTORYE ZAME^ATELXNYE PREDELY I PRAWILA RASKRYTIQ N E O P R E D E L E N N O S T E J, KOTORYE WOZNIKA@T PRI RABOTE S BES- KONE^NO MALYMI I BESKONE^NO BOLX[IMI WELI^INAMI.

1.2.3. oSNOWNYE SWOJSTWA PREDELOW

iZ RASSMOTRENNOGO WY[E SLEDUET, ^TO FUNKCIQ, IME@]AQ PREDEL, OTLI^AETSQ OT \TOGO PREDELA NA BESKONE^NO MALU@ WELI^INU, POSKOLX- KU RAZNOSTX j f(x) ; A j< " T.E. [f(x) ; A]; ESTX BESKONE^NO MALAQ WELI^INA.

1. oSNOWNAQ TEOREMA O PREDELAH.(tEOREMA O SWQZI FUNKCII S EE PRE- DELOM.)

a) pRQMAQ TEOREMA. eSLI FUNKCIQ y = f(x) PRI x ! x0 IMEET PREDE- LOM ^ISLO A TO W OKRESTNOSTI \TOJ TO^KI EE MOVNO PREDSTAWITX W WIDE SUMMY POSTOQNNOGO ^ISLA A, RAWNOGO PREDELU FUNKCII, I BESKONE^NO MALOJ WELI^INY (x) T.E.

b) oBRATNAQ TEOREMA. eSLI FUNKCI@ y = f(x) W OKRESTNOSTI TO^KI

NO PREDSTAWITX W WIDE SUMMY POSTOQNNOGO ^ISLA A I BESKONE^NO MALOJ WELI^INY (x) TO \TO POSTOQNNOE ^ISLO ESTX PREDEL FUNKCII PRI x ! x0, T.E.

ESLI f(x) = A + (x) TO A = lim f(x):

x!x0

2. eSLI FUNKCIQ IMEET PREDEL, TO TOLXKO ODIN. 3. pREDEL POSTOQNNOJ RAWEN SAMOJ POSTOQNNOJ.

4. pREDEL SUMMY (RAZNOSTI) KONE^NOGO ^ISLA FUNKCIJ, IME@]IH PREDEL, RAWEN SUMME (RAZNOSTI) PREDELOW SLAGAEMYH.

5. pREDEL PROIZWEDENIQ FUNKCIJ, IME@]IH PREDEL, RAWEN PROIZWE- DENI@ PREDELOW SOMNOVITELEJ.

6. pOSTOQNNYJ MNOVITELX MOVNO WYNOSITX ZA ZNAK PREDELA.

7. pREDEL OTNO[ENIQ DWUH FUNKCIJ, IME@]IH PREDELY, RAWEN OT- NO[ENI@ PREDELOW \TIH FUNKCIJ (PRI USLOWII, ^TO PREDEL FUNKCII, STOQ]EJ W ZNAMENATELE NE RAWEN NUL@).

11

8. pRI PREDELXNOM PEREHODE W NERAWENSTWE ZNAK NERAWENSTWA SOHRA- NQETSQ.

9. k PREDELU MOVNO PEREHODITX POD ZNAKOM L@BOJ \LEMENTARNOJ FUNKCII W OBLASTI EE OPREDELENIQ, NAPRIMER:

1.2.4. zAME^ATELXNYE PREDELY

nARQDU S UKAZANNYMI SWOJSTWAMI DLQ WY^ISLENIQ PREDELOW ISPOLX- ZU@TSQ TAK NAZYWAEMYE "ZAME^ATELXNYE PREDELY".

1. pERWYJ ZAME^ATELXNYJ PREDEL I EGO SLEDSTWIQ

pREDEL OTNO[ENIQ SINUSA BESKONE^NO MALOJ WELI^INY K SAMOJ BESKO- NE^NO MALOJ RAWEN EDINICE

sLEDSTWIQ IZ PERWOGO "ZAME^ATELXNOGO PREDELA"

1

lim (1 + (x)) (x) = e

(x)!0

s POMO]X@ WTOROGO ZAME^ATELXNOGO PREDELA RASKRYWAETSQ NEOPREDE- LENNOSTX WIDA

12