Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

4_terehina-li-fik / posobie

.PDF

Скачиваний:

Добавлен:

30.05.2015

Размер:

2.22 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1716 17 > Следующая >>>

x = 0

2: z = x4 + y4 ; x2 ; y2 ; 2xy:

1)fUNKCIQ OPREDELENA DLQ WSEH ZNA^ENIJ PEREMENNYH x I y:

2)nAHODIM ^ASTNYE PROIZWODNYE PERWOGO PORQDKA I SOSTAWLQEM SISTE- MU DLQ OPREDELENIQ KOORDINAT TO^EK, W KOTORYH WOZMOVEN \KSTREMUM

= 4x3

;

4x3

;

2y = 0

8 zx0 = 4y3

2y:

4y3

2y = 0

;

wY^ITAQ IZ PERWOGO URAWNENIQ WTOROE, POLU^IM

4(x3 ; y3) = 0 ) (x ; y)(x2 + xy + y2) = 0:

wYRAVENIE WO WTOROJ SKOBKE RAWNO NUL@ TOLXKO PRI

y = 0: pERWYJ SOMNOVITELX OBRA]AETSQ W NULX PRI x = y: pODSTAWLQEM x WMESTO y W PERWOE URAWNENIE SISTEMY I POLU^AEM

4x3 ; 4x = 0 ) x1 = 0 x2 = ;1 x3 = 1:

sOOTWETSTWU@]IE ZNA^ENIQ y y1 = 0 y2 = ;1 y3 = 1: tAKIM OBRAZOM, MY POLU^ILI TRI KRITI^ESKIH TO^KI

O(0 0) M1(;1 ;1) M2(1 1):

3) nAHODIM ^ASTNYE PROIZWODNYE WTOROGO PORQDKA I WY^ISLQEM IH W \TIH TO^KAH

	@2z				@2z			@2z
	@x2 = 12x2 ; 2					= ;2		@y2 = 12y2 ; 2:
	@x2 = 12x2 ; 2				@x@y	= ;2		@y2 = 12y2 ; 2:
1) M1(;1 ;1):		a11 = 10			a12 = ;2		a22 = 10:
				2			10 10 ; (;2)		2		= 96 > 0:
sOSTAWLQEM WYRAVENIE			a11a22 ; a12 =				10 10 ; (;2)				= 96 > 0:
sOSTAWLQEM WYRAVENIE
oTME^AEM, ^TO \KSTREMUM SU]ESTWUET I, TAK KAK, PRI \TOM, a11 > 0 {
W TO^KE	M1(;1 ;1)	; min:		: M1 zmin = z(;1 ;1) = ;2:
zNA^ENIE FUNKCII W TO^KE				: M1 zmin = z(;1 ;1) = ;2:
2) M2(1 1):		a11 = 10			a12 = ;2		a22 = 10:
				2						2	= 96 > 0:
wY^ISLQEM W TO^KE		M2 : a11a22 ; a12 = 10 10 ; (;2)									= 96 > 0:
wY^ISLQEM W TO^KE
\|KSTREMUM SU]ESTWUET I, TAK KAK, PRI \TOM, a11 > 0 { W TO^KE M2(1 1);
min: zNA^ENIE FUNKCII W TO^KE min : z(1								1) = ;2:			153

3) O(0 0): a11 = ;2 a12 = ;2 a22 = ;2:

wY^ISLQEM W TO^KE O(0 0) a11a22 ; a212 = ;2(;2) ; (;2)2 = 0: wYWOD: WOPROS O SU]ESTWOWANII \KSTREMUMA W TO^KE O(0 0) OSTAETSQ

POKA OTKRYTYM.

rASSMOTRIM ZNAK POLNOGO PRIRA]ENIQ FUNKCII W NA^ALE KOORDINAT.z(0 0)= z(x y);z(0 0)= x4+y4 ;x2 ;y2 ;2xy = x4 +y4 ;(x + y)2:

pRI y = ;x PRIRA]ENIE z(0 0) = 2x4 > 0:

pRI y = x PRIRA]ENIE z(0 0) = 2x4 ; 4x2 = 2x2(x2 ; 2) < 0: sLEDOWATELXNO, PRIRA]ENIE FUNKCII W NA^ALE KOORDINAT PRINIMAET ZNA^ENIQ RAZNYH ZNAKOW, PO\TOMU \KSTREMUMA NET.

3: z = x3 y3 (6 ; x ; y):

1)fUNKCIQ OPREDELENA NA WSEJ KOORDINATNOJ PLOSKOSTI.

2)nAHODIM ^ASTNYE PROIZWODNYE PERWOGO PORQDKA I SOSTAWLQEM SIS- TEMU DLQ OPREDELENIQ KOORDINAT KRITI^ESKIH TO^EK.

= 3x2 y3 (6

x3 y3 = x2 y3 (18

;

4x)

8 zx0 = 3x3 y2 (6

; x

; y)

; x3 y3 = x3 y2 (18

; 4y):

;

(18 ; 3y ; 4x) = 0

8 x1 = 0

y1 ; L@BOE

8 x3

< x

(18 ; 3x ; 4y) = 0

)

< y2 = 0

x2 ; L@BOE

;

3y ; 4x = 0

A TAKVE

4y = 0

x = y x3 = y3 = 18:

;

)

t.O., KRITI^ESKIMI: TO^KAMI SLUVAT WSE TO^KI OSEJ KOORDINAT I TO^KA

M0(18=7 18=7).

3) nAHODIM ^ASTNYE PROIZWODNYE WTOROGO PORQDKA I WY^ISLQEM IH W \TIH TO^KAH

z00 = 2x y3 (18 ; 3y ; 4x) ; 4x2 y3 = 2xy3(18 ; 6x ; 3y)

z00 = 3x2 y2 (18 ; 3y ; 4x) ; 3x2 y3 = 3x2y2(18 ; 4x ; 4y)

z00 = 2x3 y (18 ; 3x ; 4y) ; 4x3 y2 = 2x3y(18 ; 3x ; 6y):

154

o^EWIDNO, ^TO WO WSEH TO^KAH OSEJ

OY I

OX WSE ^ASTNYE PRO-

IZWODNYE 2-GO PORQDKA RAWNY NUL@, I WOPROS OB \KSTREMUME OSTAETSQ

OTKRYTYM. w TO^KE

M0(18=7 18=7) :

a11 =

;

4(18=7)5

a12 =

;

3(18=7)5

a22 =

;

4(18=7)5:

: a11a22

0 > 0:

pROWERQEM

; a12

= 16(18=7)

; 9(18=7)

|KSTREMUM SU]ESTWUET I, TAK KAK, PRI \TOM a11 < 0 { W TO^KE

M0(18=7 18=7) ; max:

zNA^ENIE FUNKCII W TO^KE max : zmax = (18=7)6(6 ; 36=7) 248:

4.3.3.nAIBOLX[EE I NAIMENX[EE ZNA^ENIQ FUNKCII W OBLASTI

pUSTX FUNKCIQ z = f(x y) I EE ^ASTNYE PROIZWODNYE 1-GO PORQDKA NEPRERYWNY W ZAMKNUTOJ OBLASTI (D). tAKAQ FUNKCIQ SOGLASNO TE- OREME wEJER[TRASSA DOSTIGAET W \TOJ OBLASTI SWOEGO NAIBOLX[EGO I NAIMENX[EGO ZNA^ENIJ LIBO WO WNUTRENNIH TO^KAH OBLASTI, LIBO W TO^- KAH, LEVA]IH NA GRANICE OBLASTI. eSLI NAIBOLX[EE ILI NAIMENX[EE ZNA^ENIQ FUNKCIQ PRINIMAET WO WNUTRENNIH TO^KAH OBLASTI, TO \TI TO^KI OBQZATELXNO BUDUT KRITI^ESKIMI TO^KAMI FUNKCII, PO\TOMU DLQ OTYSKANIQ NAIBOLX[EGO I NAIMENX[EGO ZNA^ENIJ FUNKCII NEOBHODIMO DEJSTWOWATX SOGLASNO SLEDU@]EJ SHEME.

1) nAHODIM KRITI^ESKIE TO^KI FUNKCII IZ USLOWIJ RAWENSTWA NUL@

PERWYH ^ASTNYH PROIZWODNYH FUNKCII z0 = 0	z0 = 0:
x	y

iZ POLU^ENNYH TO^EK OSTAWLQEM TOLXKO TE, KOTORYE PRINADLEVAT ZA- DANNOJ OBLASTI I WY^ISLQEM ZNA^ENIQ FUNKCII W \TIH TO^KAH. (hARAK- TER KRITI^ESKIH TO^EK MY W DANNOJ ZADA^E NE RASSMATRIWAEM.)

2) iSSLEDUEM FUNKCI@ NA GRANICE OBLASTI. dLQ \TOGO IZ URAWNE- NIQ GRANICY OBLASTI WYRAVAEM ODNU IZ PEREMENNYH I PODSTAWLQEM W WYRAVENIE DLQ FUNKCII z = f(x y): pOLU^AEM FUNKCI@ ODNOJ PEREMENNOJ, I ZADA^A SWODITSQ K IZWESTNOJ ZADA^E OTYSKANIQ NAIBOLX- [EGO I NAIMENX[EGO ZNA^ENIJ FUNKCII ODNOJ PEREMENNOJ W ZAMKNUTOM PROMEVUTKE.

3) iZ WSEH POLU^ENNYH ZNA^ENIJ FUNKCII W HARAKTERNYH TO^KAH OTBIRAEM PUTEM PROSTOGO SRAWNENIQ DWA ZNA^ENIQ: ODNO NAIBOLX[EE, A DRUGOE NAIMENX[EE.

155

1. nAJTI NAIBOLX[EE I NAIMENX[EE ZNA^ENIQ FUNKCII

z = 2x2 + 2xy ;

2 ; 4y

W OBLASTI (D): f y = 2x

y = 4 x = 0 g:

1) nAHODIM KRITI^ESKIE TO^KI FUNKCII

@x@z = 4x + 2y = 0

@y = 2x ; y ; 4 = 0:

rE[ENIE>

SISTEMY: x = 1

y =

;

2: iZ RISUNKA 4.7 WIDNO, ^TO KRITI-

^ESKAQ TO^KA M(1 ;2) NE PRINADLEVIT ZADANNOJ OBLASTI.

2) iSSLEDUEM FUNKCI@ NA GRANICE OBLASTI (ONA SOSTOIT IZ TREH

U^ASTKOW)

02 y

a) nA LINII OA :

x = 0

IMEEM FUNKCI@ ODNOJ

PEREMENNOJ

z = 2x2 + 2xy ;

; 4y = ;

; 4y:

i]EM NAIBOLX[EE I NAIMENX[EE ZNA^ENIQ FUNKCII

z = ; 2 ; 4y W

INTERWALE 0

;

4 = 0

)

;

(D):

pO\TOMU NAHODIM ZNA^ENIQ FUNKCII NA KONCAH INTERWALA

;24:

z(0) = 0 z(A) = z(y = 4) =

;

2 ; 4

4 =

b) nA LINII AB :

y = 4

0 x 2

IMEEM FUNKCI@ ODNOJ

PEREMENNOJ

z = 2x2 + 2xy

4y = 2x2

4 4 = 2x2 + 8x ; 24:

;

2 ;

+ 8x ;

2 ;

i]EM NAIBOLX[EE I NAIMENX[EE ZNA^ENIQ FUNKCII z = 2x2 + 8x ; 24

W INTERWALE [0 2]:

= 4x + 8 = 0

)

x =

;

(D):

nAHODIM ZNA^ENIQ FUNKCII NA KONCAH INTERWALA

z(A) = z(x = 0) = ;10 z(B) = z(x = 2) = 2

22 + 8

2 ; 24 = 0:

c) nA LINII OB :

y = 2x

0 x 2

IMEEM FUNKCI@ ODNOJ

PEREMENNOJ

z = 2x2 + 2xy

4y = 2x2

+ 4x2 ;

4x2

8x = 4x2

;

2 ;

; 8x:

i]EM NAIBOLX[EE I NAIMENX[EE ZNA^ENIQ FUNKCII z = 4x2 ;8x W

INTERWALE [0 2]:

z0 = 8x

;

8 = 0

)

x = 1

(D) :

;

8 =

;4: nA KONCAH

zNA^ENIE FUNKCII W \TOJ TO^KE

z(x = 1) = 4

INTERWALA ZNA^ENIQ FUNKCII UVE NAJDENY

z(O) = 0

z(B) = 0:

3) sRAWNIWAQ WSE POLU^ENNYE ZNA^ENIQ, OPREDELQEM

zNAIB: = z(O) = z(B) = 0

zNAIM: = z(A) = z(0 4) = ;24:

156

2. nAJTI NAIBOLX[EE I NAIMENX[EE ZNA^ENIQ FUNKCII

z = x2 + xy ; 2 W OBLASTI (D) : f y = 4x2 ; 4 y = 0 g:

	1) nAHODIM KRITI^ESKIE TO^KI FUNKCII
	8	@x@z = 2x + y = 0
	>	@z
	<	@y = y = 0:
	>
rIS. 4.8.	:
rIS. 4.8.
rE[ENIE SISTEMY: x = 0		y = 0: iZ RISUNKA 4.8 WIDNO, ^TO KRITI^ES-
KAQ TO^KA M1(0 0) NAHODITSQ NA GRANICE ZADANNOJ OBLASTI. zNA^ENIE

FUNKCII W \TOJ TO^KE z(0 0) = ;2:
2) iSSLEDUEM FUNKCI@ NA GRANICE OBLASTI (ONA SOSTOIT IZ DWUH
LINIJ).					y = 4x2 ;4 ;1 x
a) nA DUGE ABC PARABOLY								1 IMEEM FUNKCI@
ODNOJ PEREMENNOJ			z = x2 + x (4x2 ; 4) ; 2 = 4x3 + x2						; 4x ; 2:
i]EM NAIBOLX[EE I NAIMENX[EE ZNA^ENIQ FUNKCII
z = 4x3 + x2	; 4x ; 2 W INTERWALE [;1 1]:
z0 = 12x2 + 2x		;	4 = 0	)	x1 =	;	2=3 x2 = 1=2	2	(D):
x
zNA^ENIQM x	SOOTWETSTWU@T ZNA^ENIQ y1 = ;20=9							I y2 = ;3:

tAKIM OBRAZOM, MY IMEEM E]E DWE KRITI^ESKIE TO^KI NA GRANICE OB-

LASTI M2(;2=3 ;20=9) M3(1=2 ;3):

nAHODIM ZNA^ENIQ FUNKCII W \TIH TO^KAH I NA KONCAH PROMEVUTKA

z(M2) = z(x = ;2=3) =

;2=27 z(M3) = z(x = 1=2) = ;13=4:

z(A) =

z(C) = ;1:

b) nA OTREZKE AC

: y = 0 ;1 x 1 IMEEM z = x2 ;

; 2 W

i]EM NAIBOLX[EE I NAIMENX[EE ZNA^ENIQ FUNKCII z = x2

INTERWALE [

;

1 1]:

= 2x = 0

)

x = 0

(D):

tO^KU

M1(0 0)

MY UVE RASSMATRIWALI

, ( z(0 0) = ;2 ):

zNA^ENIQ FUNKCII NA KONCAH INTERWALA TAKVE UVE NAJDENY, PO\TOMU

3)	sRAWNIWAEM WSE POLU^ENNYE ZNA^ENIQ FUNKCII, OPREDELQEM
	2	20	2		1	13
zNAIB: ;3		; 9	! = ;		zNAIM: 2	;3! = ; 4	:
				27

157

4.4. sKALQRNOE POLE

4.4.1. pONQTIE SKALQRNOGO POLQ

gOWORQT, ^TO W NEKOTOROJ OBLASTI PLOSKOSTI XOY ZADANO SKALQRNOE POLE, ESLI W KAVDOJ TO^KE \TOJ OBLASTI OPREDELENA NEKOTORAQ FUNKCIQ DWUH NEZAWISIMYH PEREMENNYH

U = f(x y):

gOWORQT, ^TO W NEKOTOROJ OBLASTI 3-H MERNOGO PROSTRANSTWA ZADANO SKALQRNOE POLE, ESLI W KAVDOJ TO^KE \TOJ OBLASTI OPREDELENA NEKOTO- RAQ FUNKCIQ TREH NEZAWISIMYH PEREMENNYH

U = f(x y z):

fIZI^ESKIMI PRIMERAMI SKALQRNYH POLEJ MOGUT SLUVITX

{POLE TEMPERATUR NERAWNOMERNO NAGRETOGO TELA T = T (x y z)

{POLE ATMOSFERNOGO DAWLENIQ NA NEKOTOROM U^ASTKE ZEMNOJ POWERH- NOSTI P = P (x y)

{POLE RASPREDELENIQ WYSOTY POWERHNOSTI NAD UROWNEM MORQ

H= H(x y)

{POTENCIAL \LEKTRI^ESKOGO ILI MAGNITNOGO POLQ WOKRUG PROWODNI- KA S TOKOM ' = '(x y z):

wAVNEJ[IMI HARAKTERISTIKAMI SKALQRNYH POLEJ, ZNANIE KOTORYH

POZWOLQET NAGLQDNO PREDSTAWLQTX I ANALIZIROWATX IH, QWLQ@TSQ SLE- DU@]IE:

1.lINII I POWERHNOSTI UROWNQ.

2.pROIZWODNAQ POLQ W TO^KE W ZADANNOM NAPRAWLENII.

3.gRADIENT POLQ.

oSTANOWIMSQ PODROBNEE NA \TIH PONQTIQH.

4.4.2. lINII I POWERHNOSTI UROWNQ

lINIEJ UROWNQ SKALQRNOGO POLQ U = U(x y) NAZYWAETSQ LINIQ NA PLOSKOSTI, SOEDINQ@]AQ TO^KI RAWNYH ZNA^ENIJ FUNKCII, T.E. SEMEJ- STWO LINIJ UROWNQ NA PLOSKOSTI OPREDELQETSQ URAWNENIEM

U(x y) = const:

158

w SLU^AE PROSTRANSTWENNOGO POLQ GOWORQT O POWERHNOSTQH UROWNQ { POWERHNOSTQH, NA KOTORYH FUNKCIQ PRINIMAET ODINAKOWYE ZNA^ENIQ. uRAWNENIQ POWERHNOSTEJ UROWNQ: U(x y z) = const:

fIZI^ESKIE PRIMERY LINIJ I POWERHNOSTEJ UROWNQ:

{IZOTERMY, IZOBARY W METEOROLOGII,

{GORIZONTALI W KARTOGRAFII,

{\KWIPOTENCIALXNYE LINII I POWERHNOSTI W TEORII \LEKTROMAGNE- TIZMA.

zADA^A nAJTI I IZOBRAZITX LINII I POWERHNOSTI UROWNQ SKALQR- NYH POLEJ.

1: U = x2 ; y2:

sEMEJSTWO LINIJ UROWNQ OPREDELQETSQ URAWNENIEM

x2 ; y2 = C =)	x2 y2
	C ; C = 1:

|TO SEMEJSTWO RAWNOBOKIH GIPERBOL S ASIMPTOTAMI y = x y = ;x: w ZAWISIMOSTI OT ZNAKA WZQTOJ KONSTANTY C DEJSTWITELXNOJ OSX@ GI- PERBOL MOVET BYTX I OSX OX I OSX OY: (rIS.a)

									rIS. c
	rIS. a								rIS. b
			x
2: U =				:
		x2 + y2
sEMEJSTWO LINIJ UROWNQ OPREDELQETSQ URAWNENIEM
	x							x
			= C =) x2				+ y2 =		:
	x2 + y2							C
\|TO SEMEJSTWO OKRUVNOSTEJ S CENTROM, SME]ENNYM PO OSI WLEWO ILI
WPRAWO W ZAWISIMOSTI OT ZNAKA C NA WELI^INU j1=2Cj
1
I RADIUSOM R =						:	(rIS.b)
					(2C)2

159

z = C(x2 + y2):

3: U = x2 + y2 :

sEMEJSTWO POWERHNOSTEJ RAWNOGO UROWNQ OPREDELQETSQ URAWNENIEM z

x2 + y2 = C =)

|TO SEMEJSTWO PARABOLOIDOW, S WER[INAMI W NA^ALE KOORDINAT I SX@ SIMMETRII OZ: (rIS.c) w ZAWISIMOSTI OT ZNAKA C PARABOLOIDY MOGUT BYTX NAPRAWLENY WWERH ILI WNIZ.

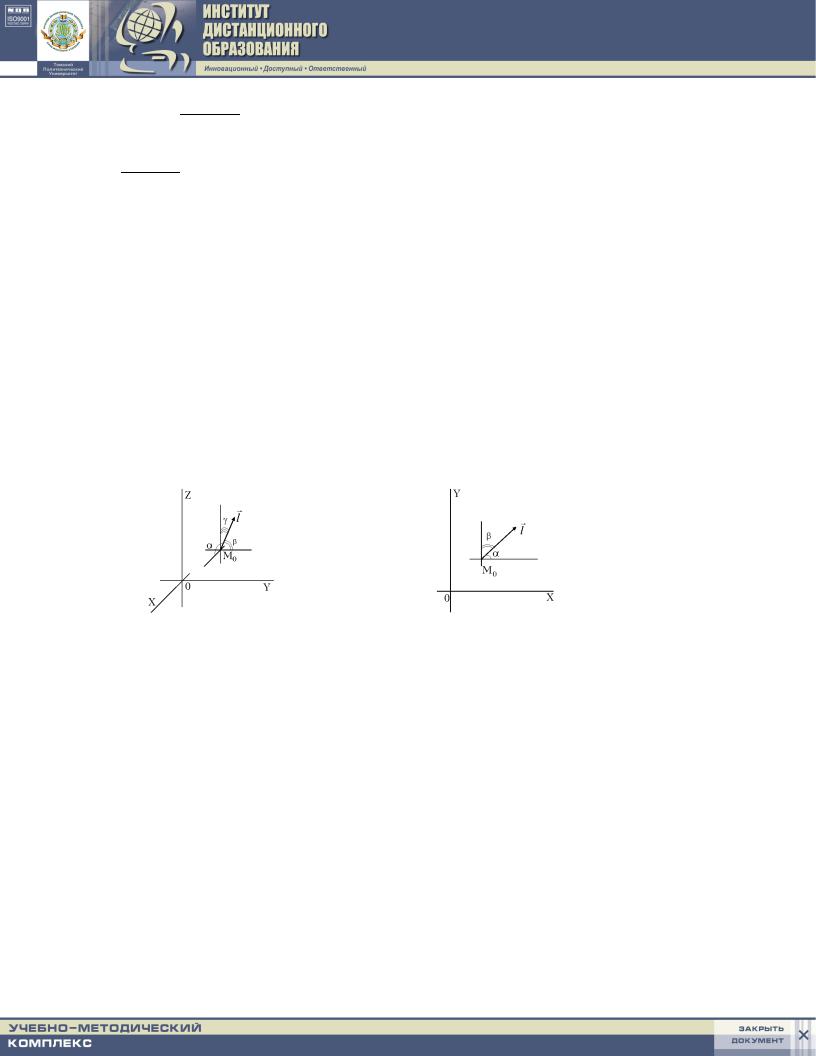
4.4.3. pROIZWODNAQ PO NAPRAWLENI@

pUSTX W NEKOTOROJ OBLASTI 3-H MERNOGO PROSTRANSTWA, SODERVA]EJ TO^KU M0(x0 y0 z0) ZADANA DIFFERENCIRUEMAQ FUNKCIQ U = U(x y z): pROSLEDIM ZA EE IZMENENIEM PRI PEREME]ENII IZ TO^KI M0(x0 y0 z0) W ZADANNOM NAPRAWLENII, HARAKTERIZUEMOM EDINI^NYM WEKTOROM ~lo OB- RAZU@]IM S OSQMI KOORDINAT OX OY OZ UGLY SOOTWET- STWENNO.

o P R E D E L E N I E. pROIZWODNOJ SKALQRNOJ FUNKCII U(x y z)
		~			M0(x0 y0 z0) NAZYWAETSQ KONE^NYJ PRE-
PO NAPRAWLENI@ l			W TO^KE		M0(x0 y0 z0) NAZYWAETSQ KONE^NYJ PRE-
DEL OTNO[ENIQ PRIRA]ENIQ U FUNKCII PRI PEREME]ENII IZ TO^KI
M0(x0 y0							~
M0(x0 y0		z0) W NAPRAWLENII WEKTORA l K WELI^INE \TOGO PEREME]ENIQ
PRI STREMLENII WELI^INY PEREME]ENIQ K NUL@
					@U	= lim	U :
					@l	!0
pROIZWODNAQ PO NAPRAWLENI@ WY^ISLQETSQ PO FORMULE
		@U@l	= @U@x cos + @U@y cos + @U@z cos
	@U	@U	@U	;
GDE	@x	@y	@z	;	^ASTNYE PROIZWODNYE FUNKCII U(x y z)
WY^ISLENNYE W TO^KE				M0		cos	cos cos ; NAPRAWLQ@]IE
160

cos + @U@y

KOSINUSY NAPRAWLENIQ ~l ILI ^TO TOVE { KOORDINATY EGO ORTA

= fcos

cos

cos g:

z g TO EGO NAPRAWLQ@-

eSLI IZWESTNY KOORDINATY WEKTORA l = f x

]IE KOSINUSY NAHODQTSQ PO FORMULAM

cos =

cos

= px

+ y

+ z

j l j

w ^ASTNOM SLU^AE PROIZWODNAQ PLOSKOGO SKALQRNOGO POLQ U(x

y) W TO^-

KE M0(x0 y0) PO NAPRAWLENI@, SOSTAWLQ@]EMU S OSQMI KOORDINAT OX I OY UGLY I SOOTWETSTWENNO, WYRAVAETSQ FORMULOJ

@U@l = @U@x cos :

tAK KAK NA PLOSKOSTI UGLY I SWQZANY SOOTNO[ENIEM= =2 ; TO MOVNO ZAPISATX

@U@l = @U@x cos + @U@y sin :

w FIZI^ESKOM SMYSLE PROIZWODNAQ SKALQRNOJ FUNKCII W DANNOJ TO^KE PO ZADANNOMU NAPRAWLENI@ ESTX SKOROSTX IZMENENIQ \TOJ FUNK- CII W DANNOJ TO^KE PO UKAZANNOMU NAPRAWLENI@.

dLQ WY^ISLENIQ PROIZWODNOJ SKALQRNOGO POLQ W DANNOJ TO^KE PO DANNOMU NAPRAWLENI@ NEOBHODIMO:

a)nAJTI ZNA^ENIQ WSEH ^ASTNYH PROIZWODNYH PERWOGO PORQDKA W DANNOJ TO^KE.

b)iZ USLOWIJ ZADA^I, ESLI NE ZADANO SRAZU, NAJTI EDINI^NYJ WEKTOR (ORT) ZADANNOGO NAPRAWLENIQ ~lo:

c)wY^ISLITX PROIZWODNU@ SOGLASNO PRIWEDENNYM WY[E FORMULAM.

rASSMOTRIM PRIMERY.

1. nAJTI PROIZWODNU@ SKALQRNOGO POLQ U = 3x2 ; 4xy W TO^KE M0(;1 4) W NAPRAWLENII, SOSTAWLQ@]EM S OSX@ OX UGOL = 2 =3.

a) nAHODIM ^ASTNYE PROIZWODNYE I IH ZNA^ENIQ W TO^KE M0

@U@x !M0 = 6x ; 4y jx=;1 y=4 = ;22

161

@U@y !M0 = ;4x jx=;1 y=4 = 4:

b) nAPRAWLENIE NA PLOSKOSTI ZADANO UGLOM : nAHODIM

cos = cos(2 =3) = ;1=2 sin = sin(2 =3) = p3=2:

c) pODSTAWLQEM WSE POLU^ENNYE ZNA^ENIQ W FORMULU DLQ PROIZWODNOJ PO NAPRAWLENI@ DLQ SLU^AQ PLOSKOGO POLQ

= @U

= 11 + 2p

cos +

sin =

;

+ 4

14 4:

nAJTI PROIZWODNU@ SKALQRNOGO POLQ

U = xpy

W TO^KE

;z y + 4z

M0(1

;2)

W NAPRAWLENII OT TO^KI M0

K TO^KE M1(;1 ;1 2):

nAHODIM ^ASTNYE PROIZWODNYE I IH ZNA^ENIQ W TO^KE

@U@x !M0

= p

jM0 = 1

= 0

z21

M0 =

4 =

@y !M0

2py ;

2 ;

;

@U@z !M0

= (;2zy + 4) jM0

= 4 + 4 = 8:

b) nAHODIM WEKTOR NAPRAWLENIQ

;;;!M0M1 = f;1

; 1 ;1

; 1 2

;

(;2)g = f;2

;2 4g:

nAHODIM EDINI^NYJ WEKTOR,

DELQ KAVDU@ KOORDINATU WEKTORA NA EGO

DLINU

;;;!M0M1

= f;p

g = f;p

M M

j;;;!0 1j

tAKIM OBRAZOM,

NAPRAWLQ@]IE KOSINUSY

cos = ;p

cos =

c) wY^ISLQEM PROIZWODNU@ PO NAPRAWLENI@

@U@l

= @U@x

cos + @U@y

cos + @U@z

cos =

18 5

= 1

! ; 3 5 ;p

! + 8 p

7 55:

iTAK,

MY NA[LI, ^TO SKOROSTX IZMENENIQ SKALQRNOGO POLQ W DANNOJ

TO^KE W ZADANNOM NAPRAWLENII RAWNA 7 55:

162

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1716 17 > Следующая >>>

Соседние файлы в папке 4_terehina-li-fik

#
30.05.2015516.46 Кб13main.pdf
#
30.05.2015444.12 Кб13main_uch_posobie.pdf
#
30.05.20152.22 Mб14posobie.PDF
#
30.05.2015700.17 Кб14programma.pdf