Тестовые задания

1. Каноническая задача линейного программирования – это …

А) все ограничения имеет форму

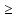
Б) все ограничения имеет форму

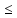
В) все ограничения имеет форму равенства Г) нет правильного ответа

2. Найти разрешающий элемент

Базис	С	План	5	4	0	0	0	0
	0	3	2	3	1	0	0	0
	0	4	1	-2	0	1	0	0
	0	5	-1	1	0	0	1	0
	0	6	5	4	0	0	0	1
		0	-5	-4	0	0	0	0

А)5 Б)-2 В)2 Г)4

3. Какого раздела не существует в математическом программировании? А) линейное программирование Б) нелинейное программирование В) целочисленное программирование Г) комплементарное программирование

4. Если задача ЗЛП имеет оптимальный план, то он достигается… А) в одной из вершин многоугольника допустимой области Б) в строке план  В) в столбце план Г) в более чем одной точке

5. К какому направлению в программировании относятся задачи , где исходная информация содержит элементы неопределенности? А) стохастическое программирование Б) выпуклое программирование В) квадратичное программирование Г) элементное программирование

6. В исходной задаче целевая функция имеет 4 переменных, а ограничения состоят из 2х неравенств, задача на max.При решении данной задачи двойственная симплекс задача имеет вид :

А)Целевая функция состоит из 3 переменных, а ограничения в системе неравенств 4х,задача на min.

Б) Целевая функция состоит из 2 переменных, а ограничения в системе неравенств 4х,задача на min.

В) Целевая функция состоит из 2 переменных, а ограничения в системе неравенств 4х,задача на max.

Г) Целевая функция состоит из 2 переменных, а ограничения в системе неравенств 3х,задача на min.

7. При решении пары взаимодвойственныхзадач СМ-решение двойственной задачи находится в …

А) первой симплекс таблице

Б) последней симплекс таблице

В)Ответ А,Б. Г)Нет правильного ответа

8.В каких случаях целесообразно применять двойственный симплекс метод?

А)Когда число ограничений прямой задачи намного больше, чем число неизвестных

Б)В задачах целочисленного программирования

В)Ответ А,Б

Г)Нет правильного ответа

9.По какому методу пересчитываются симплекс-таблицы? А)Метод треугольника Б)Метод прямоугольника В)Метод жордановых преобразований

Г)Ответ А,В Д)Ответ Б,В Е) Ответ А,Б Ж)Нет правильного ответа

10. Может ли крайняя точка выпуклого множества лежать между двумя точками на соединяющем их отрезке?

А) может;

Б) не может;

В) верно А и Б;

Г) нет правильного ответа.

11. Выпуклой линейной комбинацией точки х₁, х₂, …, х_n называется сумма:

А) α₁х₁ + α₂х₂ + … + α_nх_n ;

Б) с₁х₁ + с₂х₂ + … с_nх_n;

В) х₁ + х₂ + … + х_n ;

Г) α₁х₁ + α₂х_2.

12. Если существует набор х₁, х₂, …, х_{n ,} который удовлетворяет системе ограничений и условию неотрицательности, то он называется:

А) оптимальным решением;

Б) геометрической интерпретацией;

В) допустимым планом;

Г) допустимым значением;

Д) правильны В и Д;

Е) нет правильного ответа.

13. Симплексный метод позволяет решать ЗЛП:

А) с ограниченным числом переменных;

Б) верны А и Г;

В) с любым числом переменных;

Г) без переменных.

14.Допустимой областью решения ЗЛП графическим методом является:

А) выпуклый замкнутый многоугольник;

Б) только выпуклый замкнутый многоугольник;

В) невыпуклый замкнутый многоугольник;

Г) замкнутая окружность.

15. ЗЛП могут иметь:

А) единственное решение;

Б) неограниченное количество решений;

В) два решения;

Г) четыре решения;

Д) нет верного ответа.

16. Частным случаем допустимой областью решения ЗЛП графическим методом является:

А) только прямая и отрезок;

Б) точка, луч;

В) окружность;

Г) правильны А и Б;

Д) правильны А, Б, В.

17. Будет ли область допустимых значений выпуклым многоугольником, если система ограничений ЗЛП не противоречива:

А) будет;

Б) не будет;

В) в зависимости от условий ЗЛП;

Г) нет правильного ответа.

18. Если целевая функция исходной ЗЛП задается на максимум, то целевая функция двойственной задачи задается на:

А) максимум;

Б) минимум;

В) невозможно определить;

Г) нет правильного ответа.

19. В каком году американский математик Дж.Бернард Данциг разработал симплекс-метод?

А) в 1961 году;

Б) в 1956 году;

В) в 1949 году;

Г) нет правильного ответа.

20. Задача, в которой фигурируют ограничения в форме неравенств, называется:

А) ЗЛП;

Б) ОЗЛП;

В) транспортная задача;

Г) верны А, Б, В.

21. Линейное программирование относится к методам:

А) классической математики;

Б) математической статистики;

В) математической программирование;

Г) принятие решения в условиях неопределенности и риска.

22. Общая стоимость сырья в двойственной ЗЛП может стремится к:

А) минимуму;

Б) максимум;

В) верны А и Б;

Г) нет правильного ответа.

23. Вычислительной процедурой, основанной на принципе последовательного улучшения плана называют:

А) симплексный метод;

Б) графический метод;

В) М-метод;

Г) нет верного ответа.

24. Допустимой областью не является:

А) точка;

Б) луч;

В) прямая;

Г) незамкнутый многоугольник.

25. В оптимальном плане допустимые значения должны быть:

А) только положительные;

Б) только отрицательные;

В) положительные и отрицательные одновременно;

Г) дополнительные значения должны быть равны нулю.

26. Заполните пропуск: Множество планов общей ЗЛП является выпуклым, если оно ________ (не пусто).

27. Случай, когда в более чем в одной точке достигается оптимальный план и во всякой другой точке, являющейся выпуклой линейной комбинацией вершин многоугольника, называется:

А) случай бесконечного множества решений;

Б) случаи единственного решения;

В) случаи нулевого решения;

Г) нет верного ответа.

28. Сколько шагов в решении ЗЛП симплексным методом?

А) ровно 2;

Б) всегда 3;

В) 4;

Г) в зависимости от того, сколько шагов потребуется, чтобы удовлетворить решение при условии неотрицательности.

29.Какой вид математическогопрограммирования рассматривает методы решения задач оптимизации, в которых целевая функция является дробно линейной, а ограничения на переменные – линейные?

А) линейное программирование;

Б) дробно-линейное программирование;

В) целочисленное программирование;

Г) стохастическое программирование.

30.Установить соответствие:

1. Целевая функция линейная, все ограничения имеют вид 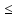0.

2. После приведения задачи к каноническому виду дополнительные переменные не образовали единичную матрицу.

3. Целевая функция представлена в виде отношения двух линейных многочленов.

4. Решение ЗЛП должно быть в целых числах.

А) дробно-линейное программирование;

Б) целочисленное программирование;

В) линейное программирование;

Г) М-метод.

1 – В, 2 – Г, 3 – А, 4 – Б.

31. Дробно-линейное программирование рассматривает методы решения задач оптимизации, в которых …

А) целевая функция линейная, ограничения на переменные линейные;

Б) целевая функция линейная, ограничения на переменные линейные и в ограничениях присутствует условие целочисленности;

В) целевая функция линейная, ограничения на переменные дробно-линейные;

Г) часть данных определяется вероятностными методами.

32. В математическом программировании существуют направления:

1. математическое программирование;

2. стохастическое программирование;

3. линейное программирование;

4. целочисленное программирование.

А) 1,2

Б) 1,2,3

В) 1,2,3,4

Г) 1,3

33. К универсальным методам ЛП относится:

А) симплексный метод;

Б) графический метод;

В) метод Монте-Карло;

Г) метод потенциалов.

34. Решения, которые позволяют достигать цели при минимальных затратах трудовых, материальных и сырьевых ресурсов, это … решения.

А) целевые;

Б) математические;

В) оптимальные;

Г) условные.

35.Модель, которая записана в математических символах, являющаяся абстракцией реального процесса, это …

А) экономическая модель;

Б) модель Кобба- Дугласа;

В) математическая модель;

Г) вероятностная модель.

36. Методы линейного программирования делятся на …

А) универсальные и приближённые методы;

Б) специальные и стохастические методы;

В) универсальные, специальные и оптимальные методы;

Г) универсальные, специальные и приближённые методы.

37.На какие два вида делится нелинейное программирование?

А) выпуклое и треугольное программирование;

Б) выпуклое и квадратичное программирование;

В) треугольное и квадратичное программирование;

Г) все ответы неверны.

38.Каким способом могут быть решены задачи ЛП с двумя переменными или сводимые к двум переменным?

А) графическим способом;

Б) математическим способом;

В) вероятностным способом;

Г) абстрактным способом.

39) Двойственный симплексный метод можно применить при решении _______________ , свободные члены уравнений, которые могут быть любыми числами.

1. метод оптимальных решений

2. задача линейного программирования

3. целочисленное программирование

4. дробно-линейное программирование

40 Если в симплексной таблице есть хотя бы один нулевой элемент (не считая свободного члена) то ЗЛП имеет признак?

А. нулевой признак

Б .признак неограниченности

В. признак бесконечности

Г. нет правильных ответов