
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •Часть I. ПРОБОЙ ГАЗОВ
- •Глава 1. Электронные и ионные процессы в газовом разряде
- •1.1. Законы сохранения энергии при столкновении атомных частиц
- •1.2. Интегральные характеристики столкновения
- •1.3. Энергия взаимодействия атомных частиц
- •1.4. Подвижность заряженных частиц
- •1.5. Диффузия заряженных частиц
- •1.6. Возбуждение и ионизация атомов и молекул
- •1.7. Термическая ионизация
- •1.8. О возможности ионизации газа ионами
- •1.9. Рекомбинация заряженных частиц
- •1.10. Термоэлектронная, автоэлектронная, взрывная эмиссия. Фотоэффект на катоде
- •1.11. Элементы кинетического уравнения для электронов
- •Глава 2. Теория пробоя Таунсенда
- •2.1. Первый коэффициент Таунсенда
- •2.2. Прилипание электронов к атомам и молекулам. Отрыв электронов от отрицательных ионов
- •2.3. Второй коэффициент Таунсенда
- •2.4. Электронная лавина
- •2.5. Условие самостоятельности разряда. Закон Пашена
- •2.6. Отступления от закона Пашена
- •2.7. Время разряда
- •Глава 3. Пробой газа в различных частотных диапазонах
- •3.1. СВЧ-пробой
- •3.2. ВЧ-пробой
- •3.3. Оптический пробой
- •Глава 4. Искровой разряд в газах
- •4.1. Наблюдения за развитием разряда в ионизационной камере
- •4.2. Схемы развития лавинно-стримерных процессов
- •4.3. Граница таунсендовского и стримерного разрядов
- •4.4. Пробой газов в наносекундном диапазоне времени
- •4.5. Длинная искра, разряд в виде молнии
- •4.6. Главный разряд
- •Глава 5. Самостоятельные разряды в газах
- •5.1. Тихий разряд
- •5.2. Тлеющий разряд
- •5.3. Дуговой разряд
- •5.4. Коронный разряд
- •5.5. Разряд по поверхности твердого диэлектрика
- •5.6. Зависимость пробивного напряжения газа от межэлектродного расстояния
- •Список литературы к разделу «Пробой газов»
- •Часть II. ПРОБОЙ ТВЕРДЫХ ДИЭЛЕКТРИКОВ
- •Глава 1. Тепловой пробой твердых диэлектриков
- •1.1. Теория теплового пробоя Вагнера
- •1.2. Другие теории теплового пробоя
- •Глава. 2. Классические теории электрического пробоя
- •2.1. Теория Роговского. Разрыв ионной кристаллической решетки
- •2.2. Разрыв твердого диэлектрика по микротрещине. Теория Горовица
- •2.3. Теория А. Ф. Иоффе
- •2.4. Теория А.А. Смурова. Теория электростатической ионизации
- •Глава 3. Квантово-механические теории электрического пробоя неударным механизмом
- •3.1. Теория Зинера. Теория безэлектродного пробоя
- •3.2. Теория Фаулера. Пробой электродного происхождения
- •3.3. Теория Я.И. Френкеля. Теория термической ионизации
- •Глава 4. Теории пробоя твердых диэлектриков вследствие ударной ионизации электронами
- •4.1. Теории Хиппеля и Фрелиха
- •4.2. Теории пробоя, основанные на решении кинетического уравнения. Теория Чуенкова
- •4.3. Некоторые замечания по теориям пробоя, основанных на рассмотрении механизма ударной ионизации электронами
- •Глава 5. Экспериментальные данные, укладывающиеся в представления о пробое твердых диэлектриков ударной ионизацией электронами
- •5.1. Стадии пробоя твердых диэлектриков
- •5.2. Развитие разряда в однородном и неоднородном полях в твердых диэлектриках
- •5.3. Эффект полярности при пробое в неоднородном электрическом поле
- •5.4. Влияние материала электродов на пробой твердых диэлектриков
- •5.5. Зависимость времени разряда от толщины диэлектрика. Формирование многолавинно-стримерного механизма разряда
- •Глава 6. Процессы, наблюдаемые в диэлектриках в области сверхсильных электрических полей
- •6.1. Электрическое упрочнение
- •6.2. Электронные токи в микронных слоях ЩГК в сильных электрических полях
- •6.3. Свечение в микронных слоях ЩГК
- •6.4. Дислокации и трещины в ЩГК перед пробоем
- •Глава 7. Другие теории пробоя твердых диэлектриков
- •7.2. Энергетический анализ электрической прочности твердых диэлектриков по теории Ю.Н. Вершинина
- •7.4. Термофлуктуационная теория разрушения твердых диэлектриков электрическим полем В.С. Дмитревского
- •7.5. Особенности пробоя полимерных диэлектриков. Теория электрического пробоя Артбауэра
- •7.6. Теория электромеханического пробоя Старка и Гартона
- •Глава 8. Некоторые особенности и закономерности электрического пробоя твердых диэлектриков
- •8.1. Статистический характер пробоя твердых диэлектриков
- •8.2. Минимальное пробивное напряжение
- •8.3. Неполный пробой и последовательный пробой
- •8.4. Кристаллографические эффекты при пробое кристаллов
- •8.5. Зависимость электрической прочности от температуры
- •8.6. Зависимость электрической прочности от времени воздействия напряжения
- •8.7. Пробой диэлектрических пленок
- •8.8. Формованные системы металл–диэлектрик–металл (МДМ)
- •8.9. Заключение по механизму электрического пробоя твердых диэлектриков
- •Глава 9. Электрохимический пробой
- •9.1. Электрическое старение органической изоляции
- •9.2. Кратковременное пробивное напряжение
- •9.3. Старение бумажной изоляции
- •9.4. Старение неорганических диэлектриков
- •Список литературы к разделу «Пробой твердых диэлектриков»
- •Часть III. ПРОБОЙ ЖИДКИХ ДИЭЛЕКТРИКОВ
- •Глава 1. Пробой жидкостей высокой степени очистки
- •1.1. Проводимость жидких диэлектриков
- •1.2. Пробой жидкостей вследствие ударной ионизации электронами
- •1.3. Пробой жидкостей неударным механизмом
- •Глава 2. Пробой жидких диэлектриков технической очистки
- •2.1. Влияние влаги
- •2.2. Влияние механических загрязнений
- •2.3. Влияние газовых пузырьков
- •2.4. Теории теплового пробоя жидких диэлектриков
- •2.5. Вольтолизационная теория пробоя жидких диэлектриков
- •2.6. Влияние формы и размеров электродов, их материала, состояния поверхности и расстояния между ними на пробой жидкостей
- •2.7. Развитие разряда и импульсный пробой в жидкостях
- •2.8. Влияние ультразвука на электрическую прочность
- •2.9. Внедрение разряда в твердый диэлектрик, погруженный в изолирующую жидкость
- •Список литературы к разделу «Пробой жидких диэлектриков»
- •ОГЛАВЛЕНИЕ
Часть II. Глава 2. Классические теории электрического пробоя
Глава. 2. Классические теории электрического пробоя
Первые исследования электрического пробоя твердых диэлектриков (ЭПТД) описаны в книге В. Франца [2]. Ван–Марум в 1799 г. наблюдал пробой в стекле в виде как бы просверленной дырки при зарядке лейденской банки. Следующий важный шаг сделал Алми, который измерил напряженность поля при ЭПТД и установил, что для пробоя стекла требуется напряженность поля 1.108 В/м, для слюды 6.2.108 В/м, для кварца (1.2÷1.5).108 В/м при толщинах 0.1 мм. Этот порядок ЭПТД (108 В/м) сохранился и по настоящее время. Значения Епр у раз-
ных авторов получались различными для одних и тех же твердых диэлектриков, что указывало на статистический характер величин Епр.
Отмечалось также, что ЭПТД отличается от теплового пробоя характером разрушения. Если при тепловом пробое твердых диэлектриков наблюдается разогрев с последующим расплавлением, то при ЭПТД разрушение обычно имеет вид как бы просверленной дырки. Появились предположения, что ЭПТД, как и газов, обусловлен ударной ионизацией электронами, но оснований к такому утверждению в то время пока еще не было.
В конце 20-х годов прошедшего века появились три более или менее обоснованных теории [1]. Это электростатический разрыв ионного кристалла (теория Роговского), теория пробоя ударной ионизацией ионами (теория А.Ф. Иоффе), теория отрыва электронов от атомов сильным электрическим полем (теория А.А. Смурова). Но эти теории требовали для пробоя напряженности поля около 1010 В/м, что на два порядка больше экспериментальных значений. Поэтому эти теории были отвергнуты. Здесь следует отметить важную роль, которую сыграла теория А.Ф. Иоффе для дальнейшего развития теорий ЭПТД. Так из теории А.Ф. Иоффе следует наличие электрического упрочнения, т.е. возрастания электрической прочности с уменьшением межэлектродного расстояния. Однако при пробое микронных слоев слюды и стекла А.П. Александров не обнаружил электрического упрочнения, что будет обсуждаться ниже. Отсутствие электрического упрочнения послужило поводом для создания теорий ЭПТД, учитывающих роль электронов, производимых неударным механизмом (теории Зинера, Фаулера, Френкеля и др.). Эти теории при полях 108 В/м давали слишком малые плотности электронного тока, так что по существу нельзя было говорить о том, что происходил пробой. Но предложенный механизм пробоя вследствие ударной ионизации электронами оставался заманчивым в теоретическом плане. К тому же появились экспериментальные дан-
103
Часть II. Глава 2. Классические теории электрического пробоя
ные, укладывающиеся в гипотезу о механизме ЭПТД вследствие ударной ионизации электронами. Так А.Ф. Вальтер и Л.Д. Инге обнаружили в щелочно-галоидных кристаллах (ЩГК) каналы неполных пробоев, а также малую длительность пробоя (10-7 с), что в дальнейшем будет еще обсуждаться. А. Хиппель также получил ряд экспериментальных данных, согласующихся с данной гипотезой (неустойчивость тока перед пробоем; развитие разряда с анода; введенные в ЩГК ионы меди остаются на своих местах и др.). Поэтому А. Хиппель первым развил теорию ЭПТД за счет ударной ионизации медленными электронами.
В 1937 г. Х. Фрелих в противоположность А. Хиппелю разработал теорию пробоя быстрыми электронами. А. Ахиезер и И. Лифшиц указали, что оба критерия (А. Хиппеля и Х. Фрелиха) неправомочны, т.к. электрическая прочность должна определяться из условия распределения энергии электронов согласно кинетическому уравнению (о чем говорилось раньше). Этим вопросом занимались ряд ученых, в том числе советских.
2.1. Теория Роговского. Разрыв ионной кристаллической решетки
Первую научную гипотезу о природе ЭПТД дал в 1927 г. Роговский. Он предположил, что электрическое поле вызывает разрыв связей между ионами в ионном диэлектрике, что приводит к его
разрушению.
В соответствии с теорией Борна потенциальная энергия взаимодействия между ионами складывается из энергии
|
|
|
q2 |
|
|
сил притяжения |
|
− |
|
|
и энергии сил |
|
|||||
|
|
|
r |
|
|
|
|
|
|
|
|
B за счет отталкивания электронных
r n
оболочек и ядер сближенных ионов и равна:
W = − |
q2 |
+ |
B |
, |
(2.1) |
|
r |
r n |
|||||
|
|
|
|
|||
где q – заряд иона, r |
– расстояние |
|||||
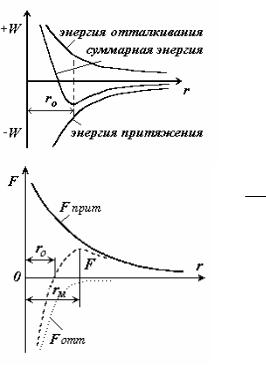
Рис. 2.1. Графики энергии и сил взаимодействия между ионами
между центрами ионов, B и n – постоянные.
Суммарная сила взаимодействия между ионами
104
Часть II. Глава 2. Классические теории электрического пробоя
F = |
dW |
= − |
q2 |
+ |
Bn |
. |
(2.2) |
|
dr |
r 2 |
r n+1 |
||||||
|
|
|
|
|
В состоянии равновесия, когда r = ro , энергия W =Wo , а сила взаимодействия между ионами
F = |
dW |
|
r=r = − |
q2 |
+ |
nB |
= 0 . |
(2.3) |
|
||||||||
dr |
|
ro2 |
ron+1 |
|||||
|
|
o |
|
|
|
|||
|
|
|
|
|
Отсюда B = q2rnоn−1 .
Электрическое поле обусловливает силу f = qE , под действием
которой будет происходить смещение ионов. Очевидно, что если сила f превзойдет силу Fм при r = rм (рис. 2.1), то ионная связь разорвется и
произойдет пробой по гипотезе Роговского. Поэтому интересно опре- |
||||||||||
делить F и r, соответствующие rм. Значение rм найдем из условия |
||||||||||
|
dF |
|
r =rм = − |
2q2 |
+ |
nB( n +1) |
= 0. |
(2.4) |
||
|
|
|||||||||
|
dr |
|
rм |
3 |
rмn+2 |
|
||||
|
|
|
|
|
|
|||||
Подставляя значение В, получим |
|||||
|
2q2 |
|
n( n +1)q2r |
n−1 |
|
|
|
= |
o |
|
|
|
rм3 |
nrмn+2 |
. |
||
|
|
||||
|
|
|
|
||
Отсюда
rм = ro n−1 n 2+1 .
Подставляя формулу (2.6) в (2.2), получаем
|
|
|
|
|
|
|
q2 |
|
|
|
|
|
|
|
|
|
q |
2r n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Fм = − |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
o |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||
|
|
n +1 |
2 |
|
|
n +1 |
n+1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
n−1 |
|
|
|
|
n−1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
r2 |
|
|
|
|
|
|
|
rn+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
о |
2 |
|
|
|
|
о |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
q2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
n+1 |
|
|
|
|
q2 n−1 |
|
(n −1) |
|
|||||||||||
|
|
|
|
|
4 |
|
|
n−1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
4 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
||||||||||||||||||||||||||
= |
|
|
− |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n+1 |
||||||||||||||||||||||
|
r2 |
|
|
(n +1)2 |
|
|
|
n + |
1 |
|
|
|
r |
2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n−1 |
|
|
||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
(n |
+ |
1) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(2.5)
(2.6)
(2.7)
Из условия Fм = qEпр определяется электрическая прочность
Епр = rq2 n+1 . (2.8)
о(n +1)n−1
Вслучае молекулы NаСl ( rо = 2.8 10−8 см, n = 9) Епр ≈1 1010 В/м. Для кристалла NаСl Роговский получил следующее. По направлениют−1 4(n −1)
105
Часть II. Глава 2. Классические теории электрического пробоя
[100] Епр = 2.9.1010 В/м, по направлению [110] Епр = 1.9.1010 В/м, по на-
правлению [111] Епр = 1.5.1010 В/м. После учета изменения постоянной решетки при сильных смещениях ионов, поляризации ионов в электрическом поле и с учетом того, что п может значительно отличаться от 9,
Роговский получил следующие соответствующие значения электриче-
ской прочности: Е100 = 1.9.1010 В/м, Е110 =1.26.1010 В/м, Е111=1.1010 В/м.
Эти значения на два порядка превышают экспериментальные значения электрической прочности ТД. Поэтому Роговский был вынужден предположить, что в реальном кристалле имеются микротрещины, которые значительно снижают величину Епр. Количественное рассмотрение возможности разрыва твердого диэлектрика по микротрещине было проведено Горовицем.
2.2. Разрыв твердого диэлектрика по микротрещине. Теория Горовица
Опыты, проведенные Горовицом, Гриффитсом и Иоффе, показали, что на поверхности твердых тел в нормальном состоянии имеются тре-
щины с глубиной порядка 10−4 см. По мнению Горовица, уже при полях порядка ~ З.106 В/м воздух в объеме микротрещины может быть ионизирован, и можно считать, что поверхность микротрещины принимает потенциал электрода.
|
|
Поскольку |
поверхности |
микро- |
|||||||
|
трещины |
приобретают |
заряд |
одного |
|||||||
|
знака, они отталкиваются друг от |
||||||||||
|
друга. Таким образом, под действием |
||||||||||
|
электрического |
поля создается |
сила |
||||||||
|
F = |
1 |
λεΕ 2 , |
которая |
стремится |
уг- |
|||||
|
|
||||||||||
|
1 |
8 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
лубить трещину. |
|
|
|
|
||||||
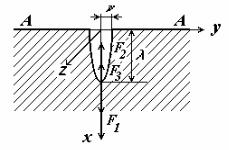
Рис. 2.2. К расчету электри- |
|
Поверхностное |
натяжение |
||||||||
характеризуется |
силой |
F2 = 2σ , |
|||||||||
ческой прочности при нали- |
|||||||||||
чии микротрещины |
которая |
препятствует |
этому. Строго |
||||||||
|
говоря, следовало бы учесть еще |
силу |
|||||||||
упругой связи ионов в решетке F3 , которая пропорциональна площади |
|||||||||||
сечения трещины и направлена как и сила F2 |
(рис. 2.2). Для очень тон- |
||||||||||
кой трещины (когда ν мала) эта сила будет стремиться к нулю и ей можно пренебречь. Когда сила электрического поля превзойдет силу поверхностного натяжения, микротрещина будет неограниченно увеличиваться, что адекватно пробою.
На основании этого было получено, что
106
