1.2. Примеры и задачи
1.2.1. Анализ термодинамических процессов
Над рабочим телом (идеальный газ) проводится термодинамический процесс.
Необходимо:
Вычислить параметры, помеченные в таблице знаком вопроса (?). Построить диаграмму процесса и ответить на вопросы.
1
)
Что означает положительное или
отрицательное значение величинQ,
L
, ΔU
и
Н?
2) Что происходит с рабочим телом и окружающей средой при изменении их состояний?
3) Возможно ли в заданном процессе совершение работы рабочим телом и одновременное увеличение его температуры?
4) Если нет (вопрос 3), то как изменяются при этом энергетические состояния рабочего тела и окружающей среды?
Обозначения:
р1,р2,V1,V2,Т1,Т2 - начальные и конечные значения давления, объема и температуры газа;Q,L- теплота и работа процесса; ΔU=U2-U1 , ΔН=Н1-Н2- изменения внутренней энергии и энтальпии газа;сv,ср- удельные изохорная и изобарная теплоемкости газа;М- масса газа;- молярная масса;R= 8314 Дж/(кмоль.К) - универсальная газовая постоянная.
Пример 1: Изотермический процесс
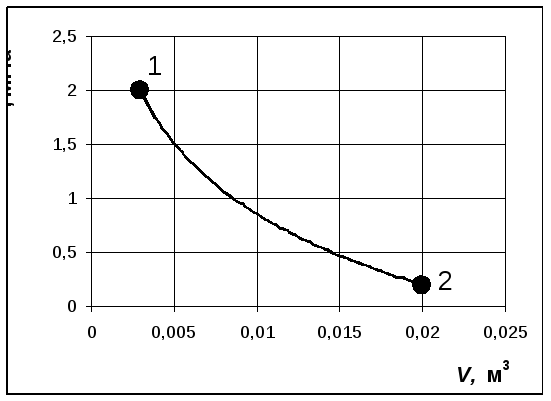
Т= 1000 К;
V1= 2·10-3м3;
V2= ?
p1= 20·105Па;
p2= 2·105Па;
L= ?
Q= ?
М= ?
μ = 32 кг/кмоль (О2).
Решение:
Напишем уравнение изотермического процесса (1.2.2): p1V1=p2V2, откуда определимV2=p1V1/p2= 20·105·2·10-3/2·105= 20·10-3м3.
Напишем уравнение состояния (1.1.1)для точки 1: p1V1= (М/μ)RТ, откуда определимМ=p1V1μ/(RТ) = 20·105·2·10-332/(8314·1000) = 15,4·10-3кг.
Работа изотермического процесса (1.2.3): L= (М/μ)RТ·ln(V2/V1) = (15,4/32)8314·1000ln(20·10-3/2·10-3) = 9212902 Дж = 9,2 МДж.
Поскольку процесс идет при постоянной температуре, изменения внутренней энергии не происходит и все подводимое тепло расходуется на выполнение работы, т.е.: Q=L= 9,2 МДж.
Для удобства построения графиков давление на нем представлено в МПа.
Пример 2: Изохорный процесс
V= 70·10-3м3;
Т1= 1200 К;
Т2= ?
p1 = 2,85·105 Па;
p2 = ?
Q = - 65000 Дж;
U2-U1 = ?
L= ?
М= 64·10-3кг;
μ = 32 кг/кмоль (О2);
сv = 1300 Дж/(кг·К).
Решение:
Т.к. изохорный процесс протекает в постоянном объеме, V=const:V1=V2= 70·10-3м3.
По количеству отведенного тепла (тепло дано со знаком -), определим конечную температуру процесса: L= 0 т. к. работа в изохорном процессе не совершается. Отведенное тепло эквивалентно уменьшению внутренней энергии:U2-U1=ΔU=Q= - 65000 Дж.
Изменение внутренней энергии (1.2.10): ΔU=Мсv(Т2-Т1), откуда:Т2=ΔU/(M·сv) +Т1= - 65000/(64·10-3·1300)+1200 = 419 К.
Напишем уравнение изохорного процесса (1.2.8): p1/Т1=p2/Т2, откуда определимр2=Т2(p1/Т1) = 419(2,85·105/1200) = 99453 = 0,99·105Па.
Пример 3: Изобарный процесс
р=p1=p2 = 20·105Па;
V1= 2·10-3м3;
V2= 10·10-3м3;
Т1= ?
Т2= ?
Q= ?
U2 – U1 = ?
H1 – H2 = ?
L= ?
M= 2·10-3кг;
μ = 2 кг/кмоль (Н2);
cvуд= 10400 Дж/(кг·К);
cруд= 14550 Дж/(кг·К).
Решение:
Напишем уравнение состояния для точки 1 (1.2.2.): pV1= (М/μ)RТ1, откуда определимТ1=pV1/ [(М/μ)R] = 20·105·2·10-3/[(2·10-3/2) 8314 ] = 481 К.
Напишем уравнение изобарного процесса (1.2.13): Т1/V1=Т2/V2, откуда определимТ2=V2·Т1/V1= 10·10-3·481/2·10-3= 2406 К.
Работа изобарного процесса (1.2.14): L=р(V2-V1) = 20·105(10·10-3- 2·10-3) = 16000 Дж.
Теплота процесса (1.2.15) Q= (U2–U1) +р(V2-V1) =Мcv(Т2–Т1) +р(V2-V1) = 2·10-3·10400(2405 – 481) + 20·105(10·10-3- 2·10-3) = 40020+ 16000 = 56020 Дж.
Изменение энтальпии (1.2.17): H1–H2=ΔH= (U2+рV2) – (U1+рV1) = (U2–U1) +р(V2-V1) =Q= 56020 Дж.
Для проверки определим количество подведенного тепла, используя изобарную теплоемкость (1.2.17): Q = Мср(Т2 – Т1) = 2·10-3·14550(2406 – 481) = 56020 Дж.