Методички / Н.Н. Демидова Физика. Методические указания по выполнению контрольных работ для студентов заочной формы обучения (сокращенные сроки обучения на базе среднего проф. образования)

70

Законы теплового излучения тел.

•Закон Кирхгофа. Отношение спектральной плотности энергетической светимости к спектральной поглощательной способности не зависит от природы тела; оно является для всех тел универсальной функцией длины (частоты) волны и температуры:

rλ, T = rλ0, T . Aλ, T

Для чёрного тела (поглощает всё падающее на него излучение) A0λ, T ≡1, поэтому универсальная функция Кирхгофа rλ0, T есть не что

иное, как спектральная плотность энергетической светимости абсолютно чёрного тела (см. рис.4.7).

•Закон Стефана – Больцмана. Энергетическая светимость абсолютно чёрного тела прямо пропорциональна четвёртой степени абсолютной температуры нагретого тела:

(задачи 4.31-4.37)

•Закон смещения Вина. Длина волны λmax , на которую приходится максимум спектральной плотности энергетической светимости чёрного тела, обратно пропорциональна абсолютной температуре:

где b = 2,9 10−3 м К - постоянная Вина (задачи 4.31-4.37). При повышении температуры Т максимум спектральной плотности энергетической светимости смещается в сторону коротких длин волн.

•Закон Вина. Максимальная спектральная плотность энергетической светимости rλmax, T чёрного тела прямо пропорциональна пятой степени абсолютной температуры:

м К

ПРИМЕР 4.5. Вследствие изменения температуры чёрного тела максимум спектральной плотности энергетической светимости rλmax,T

сместился с λ1 = 2,5 мкм на λ2 = 0,5 мкм. Во сколько раз изменилась энергетическая светимость Re нагретого тела и максимальная спектральная плотность энергетической светимости?

71

Энергетическая светимость Re чёрного тела выражается из закона Стефана – Больцмана:

Re = σ T4 ,

максимальная спектральная плотность энергетической светимости – из закона Вина:

21.Задачи 4.41-4.50 на тему «Взаимодействие фотонов с веществом»

[1, § 202-206]; [2, гл. 36]; [3, §35-37].

Свет испускается, поглощается и распространяется дискретными порциями (квантами), названными фотонами. Энергия фотона εф= hν . Его масса находится из закона взаимосвязи массы и энергии mф=hν/c2. Импульс фотона рф= hν/c .

Результат взаимодействия фотонов с электронами вещества зависит от энергии фотонов. Так, при энергии фотонов, характерных для частот видимого участка спектра (ν~1015 Гц), происходит поглощение фотона электронами вещества. Энергии поглощённого электронами фотона достаточно для разрыва связей электрона с веществом, т.е. электрон может вылететь в вакуум или другое вещество – внешний фотоэффект (задачи 4.41-4.45). Этот процесс описывается уравнением Эйнштейна:

εф = Ав+ Тmax ,

72

где с = 3 108 м/с – скорость света в вакууме; λ0 (ν0) – красная граница фотоэффекта (задачи 4.41, 4.44).

Для полного прекращения фототока (задачи 4.42, 4.43) необходимо приложить задерживающую разность потенциалов ∆ϕ З , при которой

где е = 1,6 10-19 Кл – заряд электрона; m = 9,1 10-31 кг – масса электрона.

При энергиях фотонов, характерных для частот рентгеновского участка спектра (ν ~ 1020 Гц), происходит рассеяние фотона на свободном или слабосвязанном электроне вещества – эффект Комптона (задачи 4.46-4.50). При упругом взаимодействии фотона и свободного электрона выполняются:

1) закон сохранения энергии

T = E− E0 = mc2 − m0c2 - кинетическая энергия электрона отдачи.

2) закон сохраненияr импульсаr r (рис. 4.8)

r P1 = P2 + Pe , (2)r

где P1 - импульс фотона до взаимодействия; P2 - импульс фотона по- r

сле взаимодействия; Pe - импульс электрона отдачи.

73

Совместное решение уравнений (1) и (2) даёт формулу для определения изменения длины волны фотона в результате рассеяния на свободном электроне:

где h – постоянная Планка; m0 – масса покоя электрона; с – скорость света в вакууме; θ - угол рассеяния фотона.

ПРИМЕР 4.6. В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол θ = 90°. Энергия рассеянного ε2 фотона равна 0,4 МэВ. Определить энергию ε1 фотона до рассеяния.

Выразим из этой формулы искомую энергию:

ПРИМЕЧАНИЯ 4.4:

1. Для определения доли энергии фотона (задача 4.41), расходующейся на сообщение электрону кинетической энергии, найдите отношение Т/hν.

74

2.Энергия во внесистемных единицах может измеряться в электрон - вольтах (эВ): 1 эВ = 1,6 10-19 Дж.

3.Обратите внимание на то, что ε1 = 2Е0 (задача 4.46) и ε1 = Е0

(задача 4.47), ε1 = Е0/2 (задача 4.48) и ε1 = 3Е0/2 (задача 4.50).

4. Для определения доли энергии hν фотона, приходящейся на электрон отдачи (задача 4.49), найдите отношение T/ε1.

22.Задачи 4.51-4.60 на тему «Элементы квантовой механики»

[1, гл. 28]; [2, гл. 37]; [3, гл. 9].

По идее де Бройля движение частицы связано с волновым процес-

сом.

•Формула де Бройля, выражающая связь длины волны λ с импульсом p движущейся частицы, λ = hp для двух случаев:

а) в классическом приближении (V << c); p =m0V;

б) в релятивистском случае (скорость V частицы сравнима со

Связь импульса p частицы с её кинетической энергией Т и энергией покоя Е0 = m0 c2 имеет вид

p = 1c T(T+ 2 E0 ).

Корпускулярно – волновой дуализм свойств частиц, изучаемых в квантовой механике, не позволяет с одинаковой точностью определять координату частицы, например х, и проекцию её импульса рх на ось х, энергию Е частиц в возбуждённом состоянии и время t нахождения частицы в этом состоянии.

•Соотношение неопределённостей Гейзенберга:

где значок ∆ используется для обозначения неопределённости соответствующей величины; h = 2hπ =1,054 10−34 Дж с - постоянная Планка.

Для приближённой оценки искомых величин можно полагать, что ошибки (неопределённости) в определении величин по порядку не могут быть больше самой величины.

ПРИМЕЧАНИЯ 4.5:

1. Комптоновская длина волны частицы (задача 4.51):

75

λк = mh c .

0

2.В задаче 4.52 удобнее использовать связь полной энергии

Е= mc2 и импульса р релятивистской частицы:

E2 = E02 +(p c)2

3. Используя соотношение неопределённостей для величин E и t , произведение неопределённостей которых не может быть меньше h (задачи 4,57, 4.60), учтите, что неопределённость значения энергии ∆Е

обусловлена неточностью в определении частоты излучения ∆ν фотона: ∆ν ≤ ∆hE , а интервал частот ∆ν и интервал длин волн ∆λ связаны

соотношением

∆ν = λс2 ∆λ.

4. Электрон можно считать классической частицей, если его кинетическая энергия Т много меньше энергии покоя (задача 4.56, 4.58) или его скорость V << c. Вследствие чего импульс классического электрона связан с его кинетической энергией Т соотношением

p = 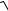2 m0 T ,

где m0 – масса покоя электрона.

23. Задачи 4.61-4.70 на тему «Радиоактивность»

[1, §254-255]; [2, §45.3-45.7]; [3, §41].

Под радиоактивностью понимают способность некоторых атомных ядер самопроизвольно превращаться в другие ядра с испусканием различных видов радиоактивных излучений и элементарных частиц. Радиоактивное излучение бывает трёх типов: α-, β-, γ- излучение.

α- излучение представляет собой поток ядер гелия; заряд α- частицы равен +2е, а масса совпадает с массой ядра изотопа 42 He .

β-излучение представляет собой поток быстрых электронов. γ-излучение является потоком частиц (фотонов).

•Закон радиоактивного распада:

N = N0 e−λt ,

где N0 – количество ядер в начальный момент времени (t = 0); N – количество не распавшихся ядер к моменту времени t; λ - постоянная радиоактивного распада (рис. 4.9).

77

Активность изотопа уменьшается со временем по закону

A = A0 e−λt .

Заменив в формуле постоянную распада λ её выражением через период полураспада, получим

ПРИМЕЧАНИЯ 4.6:

1. В задаче 4.66 обозначено число зарегистрированных частиц через ∆N1 и ∆N2 . Они связаны с первоначальным числом радиоактивных ядер:

∆N = N0 (1− e−λt )

2. В условии задачи 4.68, сказано, что активность изотопа уменьшилась на ε % , а в задаче 4.69 нужно определить, на сколько процентов уменьшилась активность. Математически это можно представить в виде

ε = A0 −A 100%. A0

Если же необходимо определить, во сколько раз уменьшилась ак-

тивность препарата (задача 4.67), исходным является соотношение A0 .

A

24. Задачи 4.71-4.80 на тему «Ядерные реакции»

[1, §262-268]; [2, §45.9]; [3, §43. 44].

•Дефект масс представляет собой разность между суммой масс покоя частиц, составляющих ядро, и массой покоя ядра:

78

∆m = Z mp + (A− Z) mn − mя,

где Z – порядковый номер элемента в таблице Менделеева (зарядовое число), который определяет число протонов в ядре; А – массовое число, определяющее суммарное число нуклонов в ядре (нуклонами называются частицы, входящие в состав ядра); mp , mn , mя – массы протона, нейтрона и ядра, соответственно. Поскольку в справочных таблицах приводятся значения масс атомов, а не ядер, то удобнее вычислять (задача 4.73) дефект масс по формуле

∆m = Z mH +(A− Z) mn −mа ,

где mH – масса покоя атома водорода; ma – масса данного атома.

•Энергия связи ядра – это энергия, которую необходимо затратить, чтобы разделить ядро на составляющие его частицы без сообщения им кинетической энергии. Энергия связи прямо пропорциональна дефекту массы системы частиц (задача 4.75):

Eсв = с2 ∆m ,

где с – скорость света в вакууме (с2 = 9 1016 м2/с2 = 9 1016 Дж/кг).

Если энергия выражена в мегаэлектрон - вольтах, а масса в атомных единицах, то с2 = 931 МэВ/а.е.м.

•При записи ядерных реакций используются следующие обозначения:

AZ X - символ ядра,

Х – символ химического элемента; А – массовое число (число нуклонов в ядре);

Z – зарядовое число (число протонов в ядре); N =A – Z – число нейтронов в ядре.

•Символическая запись ядерной реакции может быть дана в развёрнутом виде, например:

146 C+42He → 178O+01n

или сокращённо 14С(α, n)17O (задачи 4.71, 4.72, 4.80).

При сокращённой записи порядковый номер элемента не пишут, так как он определяется химическим символом атома. В скобках на первом месте записывают обозначение бомбардирующей частицы (в нашем случае α - частица), на втором –частицы, вылетающей из составного ядра (n – нейтрон) и за скобками химический символ ядра – продукта реакции.

Для обозначения частиц приняты следующие символы: p – протон, n – нейтрон, d – дейтон, t – тритон, α - альфа-частица, γ - гамма-фотон.

3.релятивистской полной энергии Er1+rE2 =rE3 +rE4 ;

4.импульса P1+ P2 = P3 + P4 .

•Энергия ядерной реакции определяется

Q = c2 [(m1+ m2 ) −(m3 + m4 )],

где m1 и m2 – массы покоя ядра мишени и бомбардирующей частицы; m3 + m4 –сумма масс покоя ядер продуктов реакции. Массы покоя атомов и частиц берутся из таблицы (см. приложение).

Если m1 + m2 > m3 + m4 , то энергия освобождается, энергетический эффект положителен, реакция экзотермическая.

Если m1 + m2 < m3 + m4 , то энергия поглощается, энергетический эффект отрицателен, реакция эндотермическая.

Энергия ядерной реакции может быть записана также в виде

(задачи 4.77, 4.79)

Q = (T1+T2 )−(T3 + T4 ),

где Т1 и Т2 – кинетические энергии соответственно ядра-мишени и бомбардирующей частицы; Т3 и Т4 – кинетические энергии вылетающей частицы и ядра – продукта реакции.

При экзотермической реакции Т3 + Т4 >Т1 + Т2 ; При эндотермической реакции Т3 + Т4< Т1 + Т2 .

ПРИМЕР 4.8. Вычислить энергию ядерной реакции:

146 C+42He → 178O+01n

РЕШЕНИЕ.

Энергия ядерной реакции определяется по формуле

Q = c2 [(mС+ mHe ) −(mO + mn )].

Из таблицы определяем массы ядер и частиц:

Подставляя в формулу, вычисляем

Q = 931 (14,00324+4,00260-16,99913-1,00867)=-1,82 МэВ.

Реакция протекает с поглощением тепла. Реакция эндотермиче-

ская.