Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

Физика

Файл:

Методички / Н.Н. Демидова Физика. Методические указания по выполнению контрольных работ для студентов заочной формы обучения (сокращенные сроки обучения на базе среднего проф. образования)

.pdf

Скачиваний:

Добавлен:

19.08.2013

Размер:

786.66 Кб

Скачать

☆

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

МИНИСТЕРСТВООБРАЗОВАНИЯРОССИЙСКОЙФЕДЕРАЦИИ КУЗБАССКИЙГОСУДАРСТВЕННЫЙТЕХНИЧЕСКИЙУНИВЕРСИТЕТ

КАФЕДРА ФИЗИКИ

ФИЗИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

для студентов заочной формы обучения (сокращённые сроки обучения на базе среднего профессионального образования)

Составители: Н. Н. Демидова Т. В. Лавряшина Э. Н. Лебединская А. А. Мальшин

Утверждены на заседании кафедры Протокол №9 от 25.06.01 Рекомендованы к печати методической комиссией направления 550600 Протокол №9 от 19.06.01 Электронная копия находится в библиотеке главного корпуса КузГТУ

Кемерово 2001

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ №1

В контрольную работу №1 включены задачи по основам механики. По каждому разделу изучаемых тем даются ссылки на учебники. Не приступайте к решению задач, не проработав теоретический материал соответствующего раздела.

1. Задачи 1.1-1.10 на тему «Кинематика поступательного и вращательного движения» [1, §1-4]; [2, гл.1, §4.1]; [3, §6].

•Перед решением задач этой темы повторите основные понятия

кинематики:

скорость V и ускорение ar при поступательном движении

тел (задачи 1.1-1.3,r

1.5, 1.6),

угловая скорость ω и угловое ускорение ε при вращательном

движении (задачи 1.4, 1.7-1.10).

•Обратите внимание на аналогию в определении кинематических

характеристик поступательного и вращательного движений.

Таблица

ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ

Скорость

d rr

Угловая скорость

dϕr

(мгновенная)

V =

(мгновенная)

d t

Модуль

V =

d rr

d S

Модуль угловой

ω =

dϕ

скорости

d t

Пройденный

S =

∫

V d t+S0

Угол поворота

ϕ =

∫

ωd t+ϕ0

путь

Среднее

Среднее угловое

∆V

∆ω

ускорение

∆t

ускорение

∆t

Ускорение

Угловое ускоре-

∆V

d V

∆ω

d ω

(мгновенное)

= lim

ние (мгновенное)

ε = lim

∆t

d t

∆t

d t

•Направление вектора средней скорости <V> определяется rнаправлением вектора перемещения ∆rr (рис.1.1). Вектор скорости V в данный момент времени направлен по касательной к траектории.

r < a

< ∆ V >

∆ V

∆ r

rr2

Рис. 1.1

Рис. 1.2

•Вектор среднего ускорения <ar> совпадает по направлению с век-

тором приращения скорости ∆V (рис. 1.2).

•Направление вектора полного ус-

корения ar, равного векторной сумме

аτ (аτ<0)

тангенциального aτ и нормального an

rτ

ускорений зависит, от величины этих

аτ (аτ>0)

ускорений (рис. 1.3)

аn

где rτ -

ar = an nr+ aτ rτ,

единичный вектор (орт), на-

правленный по касательной к траекто-

Рис. 1.3

рии (по скорости); nr

- единичный вектор

(орт) нормали к траектории (перпендику-

dω

лярно скорости); a

– проекция ускоре-

< 0 (ε < 0)

aτ - проекция

ния на вектор нормали n ;

dϕ

ускорения на вектор скорости.

dϕr

•При вращательном движении векто-

ры dϕ ,

и ε направлены вдоль оси

dω

> 0 (ε > 0)

вращения (рис. 1.4), причём направление

вектора угла поворота dϕr

связано с на-

Рис. 1.4

правлением вращения правилом правого винта.

ПРИМЕР 1.1. Точка движется по окружности радиусом R =10 см так, что зависимость линейной скорости V от времени t даётся уравнением V = A - B t2, где A = 5 м/с, В = 1 м/с2. Определить: 1) пройденный путь S1, средние значения скорости <V> и ускорения <a> за 2 с от начала движения; 2) тангенциальное аτ , нормальное аn и полное а ускорение точки в конце второй секунды; 3) угловую скорость ω и угловое ускорение ε в конце второй секунды.

Дано:

R =10 см V = A - B t2

A = 5 м/с

В = 1 м/с2 t1 = 2 c

S1, <V>, <a>, аτ, аn, а, ω, ε -?

			РЕШЕНИЕ.
1) Путь S1, пройденный за время 2 с:
t	t					t		t
S1 = ∫1	V(t) d t = ∫1	(A− B t2 ) d t = ∫1					A d t− ∫1 B t2 d t =
t0	0				0			0
t	t			t3		2			8
t	t					2
= A ∫1 d t− B ∫1 t2 d t =A t			02 − B				= 5 2	−1			= 7,4 м.


										3

0	0	3				0
0	0	3				0

Средняя скорость <V> движения точки за указанный период времени:

< V >=	∆S	=	S1	−S0	=	7,4	= 3,7	м	.
	∆t		t1	− t0		2
								с

Среднее ускорение <а> движения точки:

< а >=	∆V	=	V1− V0	=	1−5		= −2	м	.
	∆t					2
			t1− t0					с2

1) Тангенциальное ускорение аτ характеризует быстроту изменения скорости по величине:

aτ = ddVt = −2 B t = −2 1 2 = −4 см2 .

Нормальное ускорение аn характеризует быстроту изменения скорости по направлению и связано с линейной скоростью V и радиусом R окружности соотношением

			an	=	V2	.
Следовательно:			an	=	R	.
					R
	an = (A− B t2 )2			= (5 −1 4)2				=10	м	.
	an = (A− B t2 )2			= (5 −1 4)2				=10		.
	r	R	r		r0,1		r	r	с2
Полное ускорение a		= an n+ aτ τ, где τ						и n - единичные векторы
(орты). Величина полного ускорения									м .
	a = a2τ + an2		=	16 +100 =10,8					м .
									с2
Направление векторов ar, тангенциального aτ и нормального an

изображено на рис. 1.3 (случай аτ<0).

2) Угловая скорость ω связана с линейной скоростью V и радиусом R

окружности ω = VR . Вычисления дают ω = A+RB t2 =10 радс .

Угловое ускорение ε может быть определено по известному зна-

чению тангенциального ускорения аτ:
ε =	аτ	= −40	рад	.

r	R r		с2

Направления векторов ω и ε изображены на рис.1.4 (случай ε< 0).

ПРИМЕЧАНИЯ 1.1:

1.В задаче 1.1 при определении скорости V и координаты Х учтите начальные условия: V = ∫a(t) d t + V0 и X = ∫V(t) d t + X0 .

2.Для определения средней путевой скорости (задача 1.3) необходимо найти время поворота из условия V(tпов )= X′ = 0 и координату

поворота Xпов =1+ 4 tпов− 2 tпов2 .

3. Решая задачи 1.r4, 1r.7,r1.8,r1.10, обязательно укажите на рисунке направления векторов V, a , ω и ε.

2. Задачи 1.11-1.20 на тему «Законы Ньютона»

[1, §5-8]; [2, §2.1-2.4]; [3, §2].

При решении задач 1.14, 1.15, 1.17 –1.20 данного раздела рекомендуется придерживаться следующего порядка:

•Сделать рисунок и на нём изобразить все силы, действующие на данное тело. Указывая силы, необходимо руководствоваться третьим

законом Ньютона:	r	r
	F12	= −F21

силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению.

•Силы могут действовать на это тело только со стороны каких-либо

других тел:
со стороны Земли – сила тяжести m gr	;
r
со стороны нити – сила натяжения T ;	r
со стороны поверхности - реакция опоры N ;
r
и сила трения Fтр.

Следовательно, к данному телу приложено столько сил, сколько имеется тел, с которыми оно взаимодействует.

•Записать второй закон Ньютона в векторной форме для каждого тела:

∑n Fri = m ar.

i=1

Равнодействующая всех сил, приложенных к телу, равна произведению массы тела на его ускорение.

•Выбрать две взаимно перпендикулярныеr оси X и Y, одну (Х) из которыхrнаправляют вдоль ускорения a , другую (Y) –перпендикулярно вектору a . Спроектировать векторы на эти оси и записать второй закон Ньютона в скалярной форме:

n	n
∑Fx i = m ax , ∑Fy i = m ay .
i=1	i=1

•Если тела связаны нитью, переброшенной через блок, и массами нити и блока можно пренебречь (задачи 1.14, 1.17, 1.20), то силы натяжения одинаковы по всей длине, а вследствие нерастяжимости нитей модуль ускорения всех движущихся тел одинаков.

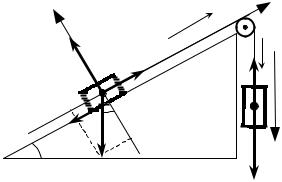
ПРИМЕР 1.2. На наклонной плоскости, составляющей с горизонтом угол α = 30°, находится груз массой m2= 2 кг. К грузу привязан лёгкий шнур, перекинутый через блок, укреплённый на вершине наклонной плоскости. К концу шнура подвешена гиря массой m1= 2,5 кг. Предоставленная самой себе система приходит в равноускоренное движение. Определить ускорение грузов при условии, что коэффициент трения между грузом и плоскостью равен µ = 0,1. Массу блока не учитывать.

Дано:				РЕШЕНИЕ.
α = 30°		В данном примере гиря будет опускаться, а груз подниматься
m2= 2 кг		по наклонной плоскости (рис.1.5)r. На гирю действуют: сила
m1= 2,5	кг	тяжести m gr	и сила натяжения T		, на груз действуют: сила
µ = 0,1		1	r	1	r	r
		натяжения шнура T2		, реакция опоры N , сила трения		Fтр, си-

а - ?		ла тяжести m2 gr. Второй закон Ньютона для каждого тела в

	r
	F	α
		α
α		r

Рис. 1.5

Х	векторной форме:				r
r	r		r		r
a1	m1 g+ T1			= m1 a1		,
T	m1 g+ T1			= m1 a1		,	r
T	r		r	r		r	r
r	m2 g+ T2 + Fтр+ N = m2 a2 ,
	m2 g+ T2 + Fтр+ N = m2 a2 ,
	в проекциях на оси X и Y с учётом того,
	что T1 = T2	= T и a1 = a2 = a ,					(1)
Х	m1 g−T = m1 a ,						(1)
Х
r

6
− m2 g sinα + T− Fтр = m2 a ,	(2)
− m2 g cos α+ N = 0.	(3)

Сила трения Fтр = µ N или, принимая во внимание уравнение (3):

		Fтр = µ m2 g cos α.								(4)
Подставим уравнение (4) в уравнение (2):
	− m2 g sin α+T−µ m2 g cosα = m2 a									(5)
Выразим силу натяжения T из уравнения (1) и (5) и приравняем
полученные выражения:		m1 g− m1 a = m2 a+ m2 g sin α+µ m2 g cos α
Находим ускорение		a =	m1 g− m2 g sin α−µ m2 g cos α						.

Произведём вычисления:				m1+ m2

	2,5 кг− 2кг sin 30o −0,1			2 кг cos30o		м			м
a =					10		= 3,0			.
	2,5 кг+ 2 кг					с2		с2

ПРИМЕЧАНИЯ 1.2:

1.Решение задач 1.11-1.13, 1.16, 1.19 не вызовет затруднений, если дополнительно воспользоваться формулами из таблицыr .

2.В задачах 1.11, 1.13 учтитеr, что импульсом Pтелаrназываютr произведение массы m на скорость Vдвижения этого тела: P = m V. В проекции на ось Х: Px = m Vx

3.Задачи 1.21-1.30 на тему «Законы сохранения импульса

имеханической энергии» [1, §9-15]; [2, §5.1, 5.2]; [3, §2].

•Закон сохранения импульса: суммарный импульс замкнутой системы тел (когда извне не действуют другие тела) остаётся постоянным

	r	n r	n	r
	P = ∑Pi = ∑miVi = const ,
r	r	i=1	i=1
где Pi = miVi - импульс i –го тела.

•Закон сохранения механической энергии: полная механическая энергия тела Е системы тел, в которой действуют только консерватив-

ные силы, есть величина постоянная

E = T+ П,

где T = m2V2 - кинетическая энергия тела, движущегося поступатель-

но со скоростью V; П = m g h - потенциальная энергия тела, поднятого

вблизи поверхности Земли на высоту h относительно нулевого уровня.

•Законы сохранения импульса и механической энергии применяются для определения скоростей при абсолютно упругом ударе тел (за-

дачи 1.25-1.27, 1.30)		r			r		r			r
	m1 V1+ m2 V2					= m1 U1+ m2				U2 ,
	m V2			m	V2		m U2		m	2	U2
		1 1	+		2 2	=	1 1	+		2	2	.
		2	+		2	=	2	+		2		.
		2			2		2			2

Потенциальная энергия тел до и после взаимодействия не изменяется. Совместное решение этих уравнений позволяет получить формулы для

скоростей U1			и U2 абсолютно упругих шаров после удара:
U	=	V1	(m1− m2 )+ 2 m2 V2	, U	2	=	V2 (m2 − m1 )+ 2 m1 V1	.

1			m1+ m2				m1+ m2

•При абсолютно неупругом ударе (задачи 1.21-1.24, 1.28, 1.29) вы-

полняется только закон сохраненияr r импульса: r

m1 V1+ m2 V2 = (m1+ m2 ) U,

а закон сохранения механической энергии не выполняется, так как часть её расходуется на совершение работы деформации Адеф (выделяется в виде тепла Q):

m V2

+ m

) U2

1 1

+ Адеф

ПРИМЕР 1.3. Два свинцовых шара

массами m1 = 1 кг и m2

=3 кг подвешены

на одинаковых нитях

длиной l

= 1 м.

l− h

Нить с меньшим шаром отклонили на угол

α = 60° от вертикали и отпустили (рис.

r r

1.6). Считая удар центральным и неупру-

гим, определить энергию, израсходован-

U V1

h = 0

ную на деформацию шаров при ударе.

Рис. 1.6

Дано:

РЕШЕНИЕ.

m1 = 1 кг

При абсолютно неупругом ударе выполняется только закон

m2 = 3 кг

= (m + m

сохранения импульса: m V + m

) U,

l = 1 м.

2 2

где V - скорость первого шара до удара;

= 0 - скорость

α = 60°

Wдеф - ?

второго шара до удара; U- общая скорость шаров после удара.

Проектируем уравнение (1) на ось Х: m1 V1 = (m1+ m2 ) U .

Скорость первого шара до удара V1 определим из закона сохранения механической энергии. Для системы «шар – Земля» действуют только консервативные силы (сила тяжести, сила упругости). Силой сопротивления среды пренебрегаем. В начальном положении I полная механическая энергия равна потенциальной m1gh (отсчёт высоты ведётся от уровня h = 0, соответствующего положению равновесия шаров). В положении II перед ударом шаров полная механическая энергия системы равна кинетической энергии шара. Следовательно:

m1 g h = m12V12 .

Откуда скорость первого шара до удара V1 = 2g h . Высоту h определяем из тригонометрического соотношения

l − h = l cos α, тогда V1 = 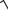2g l (1−cos α) .

Общая скорость шаров после неупругого удара:

U =	m1 V1		=	m1		2g l (1−cos α) .
	m + m	2		m + m	2

	1			1

Энергия деформации при неупругом ударе Wдеф определяется разностью кинетических энергий шаров ТI и ТII до и после удара:

m V2

= m g l (1−cos α)

m12

m1+ m2

g l(1−cos α)

m1+ m2

Следовательно:

m1 m2 g l (1− cos α)

= T

− T

= m g l (1− cos α) 1

−

деф

+ m

Произведём вычисления:

1кг 3кг 10м/с2 1м (1−cos 60o)= 3,75 Дж.

деф

1кг+3кг

ПРИМЕЧАНИЯ 1.3:

1. Закон сохранения импульса применяется для системы «пуляшар» (задачи 1.21, 1.28) и системы двух шаров (задача 1.22), а закон сохранения механической энергии для системы «шар с пулей – Земля»

(задачи 1.21, 1.28) и «шар – Земля» (задача 1.22).

2. При решении задачи 1.23 дополнительно учтите, что кинетическая энергия тележки с человеком расходуется на работу против сил трения:

T = Aтр = Fтр S .

3. В задачахr 1.25, 1.26 rучтите,rчто до взаимодействия снаряд и орудие покоятся P0 = 0 = m1 V1+ m2 V2 .

4. Задачи 1.31-1.40 на тему «Расчёт моментов инерции различных тел» [1, §16]; [2, §4.3]; [3, §3].

•Момент инерции твёрдого тела или системы материальных точек относительно оси вращения существенно зависит от характера распределения массы относительно этой оси.

•При дискретном распределении массы (задача 1.32) момент инер-

ции системы относительно оси вращения определяется суммой моментов инерции Ii материальных точек массой mi , находящихся на расстоянии ri от оси:

n	n
I = ∑Ii = ∑mi ri2		(1)
i=1	i=1

•При равномерном распределении массы твёрдого тела момент его инерции относительно оси вращения определяется формулой

I = ∫r2 d m,	(2)
m

где r – расстояние от элемента до оси вращения; dm – масса бесконечно малого элемента, на которые мысленно разбивается тело.

•Распределение массы по длине стержня (проволоки) характеризуется линейной плотностью τ (задачи 1.31, 1.33, 1.37-1-40):

τ =	d m	,	[τ]=	кг	.	(3)
	d l
				м

•Распределение массы пластины (диска) характеризуется поверхностной плотностью σ (задачи 1.34 - 1.36):

σ =	d m	,	[σ]=	кг	.	(4)
	d S
				м2

Применяя формулы (2) и (3) для расчётов моментов инерции тел с линейным распределением массы, учтите расположение стержня относительно оси вращения.

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в папке Методички