
Методички / Н.Н. Демидова Физика. Методические указания по выполнению контрольных работ для студентов заочной формы обучения (сокращенные сроки обучения на базе среднего проф. образования)
.pdf
|
r |
|
50r |
r |
r |
d F = d Fx i |
+ d Fy j , |
||
r |
|
|
r |
|
где i |
и j - единичные орты; dFx и dFy - проекции вектора B на коорди- |
|||
натные оси.r |
|
|
|
|
|
Сила F, действующая на проводник: |
|||
|
r |
r |
|
r |
|
F = i ∫d Fx |
+ j ∫d Fy |
||
и ее величина (модуль) F = |
F2 |
+ F2 |
, |
|
|
|
x |
y |
r |
где Fx = ∫d Fx = ∫cosβ d F, |
|
|
||
Fy = ∫d Fy = ∫sin β d F - проекции силы F |
||||
на координатные оси. Так как переменные dl и β связаны соотношением d l = R dβ, то
β1 |
β1 |
Fx = ∫I B R cosβ dβ, |
Fy = ∫I B R sin β dβ. |
0 |
0 |
Пределы интегрирования определяются условием задачи.
3. |
Прямолинейный проводник |
|
|
|
|
|
|
|
|
|
|
|
|
|||
с током I1 помещен в неоднородное |
|
|
|
|
|
|
|
|
|
|
|
b |
||||
магнитное поле, созданное, напри- |
|
|
|
|
|
|
|
|
|
|
||||||
мер (задачи 3.37, 3.39, 3.40), беско- |
|
|
r |
|
|
|
|
r |
|
|
|
|||||
нечно |
длинным прямолинейным |
|
|
|
I2 |
|
|
|
I1 |
|||||||
|
|
|
B2 |
|
|
B2 |
||||||||||
проводником с током |
I2 (рис.3.7). |
|
|
|
|
|
|
|
|
|
|
|
||||
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величина силы Fab , действующей |
|
|
|
|
|
|
|
|
r0 |
|
|
|||||
на часть ab проводника, располо- |
|
|
|
|
|
|
|
|
|
|
a |
|||||
женную |
параллельно |
бесконечно |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
длинному проводнику: |
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.16 |
||||
|
l |
l µ µ |
0 |
I I |
2 |
|
|
µ µ |
0 |
I I |
2 |
l |
|
|||
|
Fab = ∫B I1 d l = ∫ |
|
|
1 |
d l = |
|
|
1 |
|
, |
||||||
|
2 πr |
|
|
2 πr |
|
|
||||||||||
|
0 |
0 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
I1  c
c
r
Fbс
r
Fab
где l - длина участка проводникаr .
Величина силы Fbc , действующей на участок bc проводника:
l |
rc |
µ µ |
0 |
I I |
2 |
|
µ µ |
0 |
I I |
2 |
|
r |
|
Fbс = ∫B I2 d l = ∫ |
|
1 |
d r = |
|
1 |
ln |
c |
, |
|||||
2 πr |
|
|
2 π |
|
r |
||||||||
0 |
rb |
|
|
|
|
|
|
|
|
|
|
b |
|
где rb и rc - расстояния от проводника с током I2 до концов участка bc проводника с током I1.

|
|
|
|
|
|
|
|
51 |
|
|
|
|
|
•Сила взаимодействия двух бесконечно длинных прямолинейных |
|||||||||||
проводников с током I1 и I2, находящихся на расстоянии r0 друг от дру- |
||||||||||||
га, |
рассчитанная |
на |
отрезок длиной l |
|
r |
|
r |
|||||
(задачи 3.37, |
3.39, |
|
3.40), |
выражается |
|
|
||||||
|
r |
F13 |
2 |
|||||||||
|
F |
|||||||||||
формулой |
|
|
|
|
|
|
|
F1 r |
|
|
21 |
|
|
|
|
|
|
|
|
|
r |
|
|||
|
|
|
µ µ |
|
I I |
|
l |
|
F12 |
1 |
|
|
|
F |
= |
0 |
2 |
|
F23 |
|
|||||
|
|
1 |
|
, |
|
r |
|
r |
||||
|
12 |
|
2 πr |
|
|
|
|
F32 |
|
F2 |
||
|
|
|
|
|
0 |
|
|
|
|
|
r |
|
а сила их взаимодействия на единицу |
|
|
|
|||||||||
|
3r |
F3 |
|
|||||||||
длины: |
|
|
|
|
|
|
|
|
|
|
||
F |
= µ µ0 I1 I2 |
(имеет размерность Н/м). |
|
F31 |
|
|
||||||
l |
2 πr |
|
|
|
|
|
|
|
|
Рис. 3.17 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
При решении задачи 3.37 удобно рассмотреть сечение проводников перпендикулярной плоскостью и указать направление токов в них:
I - ток течет «к нам»; |
+ I - ток течет «от нас» (рис. 3.8). |
|
|
|
|
|
||||||||||||
•Квадратная рамка (задача 3.38) находится в однородном магнит |
||||||||||||||||||
ном поле |
длинного |
проводника |
|
|
N |
|
|
|
r |
|
|
|
|
|
||||
(рис. 3.9). |
|
|
|
|
|
|
|
|
|
Fab |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|||||
Определяя силу, действующую на |
|
|
|
|
|
|
|
r |
||||||||||
|
r r |
r |
r |
r |
I1 |
|
|
|
I2 |
|
|
r |
|
|
|
Fbc |
||
|
|
|
|
|
|
|
|
|||||||||||
рамку: |
F = Fab + Fbc |
+ Fcd + Fda , |
|
|
r |
|
|
|
|
B1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
учтите, что направление сил зависит от |
|
|
Fda |
|
|
|
|
|
|
|
I2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
r |
|
|
d |
|
c |
|
|
|||||||||||
выбранного направления токов в про- |
|
|
|
|
|
|||||||||||||
B1 |
|
|
|
|
|
|
r |
|
|
|
|
|
||||||
воднике MN и рамке abcd. Стороны ab и |
|
|
M |
|
|
|
|
Fcd |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
cd расположены одинаково относитель- |
|
|
|
|
Рис. 3.18 |
|
|
|
|
|
||||||||
но проводника, а токи в них |
|
|
|
|
|
|
|
|
|
|
r |
|
и |
|||||
текут в противоположных направлениях. Следовательно, силы |
F |
|
||||||||||||||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ab |
|
|
Fcd , действующие на указанные стороны рамки, численно равны и про-
тивоположно направленыr r r . Равнодействующая всех сил, приложенных к рамке, равна: F = Fbc +rFda , r
причем модули сил Fda и Fbc различны, т.к. неодинаковы индукции магнитного поля в месте расположения проводников da и bc.
ПРИМЕЧАНИЯ 3.4:
1. При решении задач 3.31, 3.33, 3.35 учтите, что величина силы Ампера максимальна, если проводник с током расположен перпендикулярно полю.

52
2. В задаче 3.31 дополнительно используйте формулу для расчета индукции магнитного поля внутри бесконечно длинного соленоида: B = µ µ0 I n , где I - ток соленоида; n - число витков на единицу длины
соленоида.
3. В задачах 3.32, 3.33, 3.39 используйте условие равновесия проводника с током, находящегосяr в скрещенных магнитном и гравитаци-
онном полях: m gr+ FA = 0, или в проекции на оси У:
I Bl = m g.
Масса m проводника выражается через плотность материала: m = ρV = ρSсеч l = ρπr2 l,
где V-объем проводника; Sсеч - площадь поперечного сечения его; r- радиус проводника.
4. Определяя работу в задаче 3.40, учтите, что сила взаимодействия параллельных проводников с токами зависит от расстояния F=F(x), а работа, которую нужно совершить, чтобы изменить расстояние между проводниками от d1 до d2 , определяется интегрированием:
A = d∫2 µ µ02Iπ1 I2 l dxx .
d1
13. Задачи 3.41-3.50 на тему «Сила Лоренца. Движение заряженных |
|||
частиц в магнитном поле» [1, §114]; [2, §23.1]; [3, §23]. |
|
||
•Сила Лоренца |
r |
|
|
F действует на частицу с зарядом q, движущуюся |
|||
r |
л |
r |
|
со скоростью V в магнитном поле индукцией B: |
|
||
|
r |
r r |
|
|
Fл = q [V , B], |
|
|
величина которой Fл = q V Bsin α, |
r |
r |
|
где α - угол между направлениями векторов скорости V и индукции B магнитного поля.
В условиях задач данной темы скорость частицы направлена перпендикулярно силовым линиям магнитного поля (α = π/2, sinα =1), поэтому
|
|
Fл = q V B. |
|
Согласно второму закону Ньютона: |
|||
|
|
m a = q V B, |
|
где a = an = |
V2 |
- нормальное ускорение, направленное по радиусу к |
|
R |
|||
|
|
||

r 53 r
центру траектории. Поскольку B = const, V = const, то траекторией движения частиц будет окружность радиуса R:
m V2 = q V B. R
ПРИМЕЧАНИЯ 3.5:
3.Характеристики элементарных частиц (электрона, протона, α-частицы) смотри в приложении.
4.Частица массой m, движущаяся со скоростью V, имеет кинети-
ческую энергию W(задачи 3.41, 3.43): W = m2V2 .
Такую энергию заряженная частица может приобрести, пройдя в электрическом поле ускоряющую разность потенциалов ∆ϕ (задачи
3.45, 3.48):
W= q ∆ϕ = m2V2 .
5.Период Т обращения частицы (задача 3.44)-это время, за кото-
рое частица, движущаяся со скоростью V, совершает полный оборот по окружности радиуса R: T = 2 πVR .
6. Частота n обращения частицы (задача 3.47) обратно пропор-
циональна периоду обращения: n = T1 = 2 VπR .
7. Удельный заряд частицы (задача 3.46) определяется отношением заряда q частицы к ее массе m.
14. Задачи 3.51-3.60 на тему «Магнитный поток. Работа по перемещению контура с током в магнитном поле» [1, §121]; [2, §22.5]; [3, §25].
Для решения задач данной темы необходимо знать следующее:
•Магнитный поток Ф, пронизывающийr контур (площадью S), находящийся в магнитном поле B, определяется по формуле
Ф = BS cos α, r |
nr к контуру. |
где α - угол между направлением вектора B и нормалью |
|
Обратите внимание, что в условии задач 3.54, 3.55, 3.59 |
задан угол ϕ |
|
r |
между плоскостью контура и вектором магнитнойrиндукции B. Поэтому угол между нормалью nr к контуру и вектором B определяется

54
α = |
π |
−ϕ . |
|
2 |
|||
|
r |
В задаче 3.51 угол между плоскостью контура и вектором B обо-
значить через ϕ.r
•Индукция B магнитного поля соленоида определяется по формуле B = µ µ0 I n , где n - число витков на единицу длины соленоида, которое
связано с диаметром d проволоки (задача 3.56), как n = Nl = dll = d1 ,
так как l = N d ; N-число витков соленоида.
•Работа внешних сил по перемещению контура с током из магнитного поля в область, где оно отсутствует (задачи 3.52, 3.60), и изменению ориентации контура (задачи 3.53, 3.57, 3.58) определяется по формуле
A = −I ∆Ф = I (Ф1−Ф2 ),
где I - сила тока в контуре; Ф1 и Ф2 –магнитные потоки, пронизывающие контур в начальном и конечном его положениях. Если контур свободноrустановился в магнитном поле (задачи 3.53, 3.57, 3.58), то нормальrn к контуру совпадает с направлением вектора магнитной индук-
ции B (угол α = 0, cosα = 1).
15. Задачи 3.61-3.70 на тему «Явление электромагнитной индукции.
Самоиндукция» [1, §122-127]; [2, гл. 25]; [3, §25].
•При всяком изменении магнитного потока сквозь контур в нем возникает электродвижущая сила индукции, пропорциональная скорости изменения магнитного потока:
Εi = − ddФt .
Знак минус отражает правило Ленца, позволяющее определить направление индукционного тока в контуре.
•Магнитный поток может изменяться:
1)при изменении ориентации контура в магнитном поле
(задачи 3.62, 3.63, 3.66, 3.69, 3.70);
2)при движении проводника в магнитном поле (задача 3.68);
3)при изменении тока в контуре (задачи 3.61, 3.64, 3.65, 3.67). При решении задач 3.61, 3.69, 3.70 используйте закон электромаг-
нитной индукции, учитывая, что магнитной поток, пронизывающий контур, содержащий N витков, определяется по формуле Ф = BSN.

55
•Если контур вращается в магнитном поле с угловой скоростью ω, то магнитный поток Ф = BScos ωt . Трудностей при решении задач
3.62, 3.66, в которых требуется определить величину протекающего по контуру количества электричества, можно избежать, если вспомнить:
1) закон Ома для замкнутого контура: I = ΕRi ,
где Ei – ЭДС, возникающая в контуре; R - его сопротивление;
2) зависимость сопротивления проводника от материала и геомет-
рических размеров: |
R = ρ |
l |
, |
|
|||
|
|
S0 |
|
где ρ - удельное сопротивление материала проводника; l - длина проводника; S0 - его поперечное сечение.
•Cамоиндукцией называется возникновение ЭДС индукции в контуре при изменении силы тока в нем. Среднее значение ЭДС самоиндукции, возникающей в проводящем контуре, определяется скоростью
изменения силы тока |
∆I |
в нем: |
Εi |
= −L |
∆I |
, |
|
∆t |
∆t |
||||||
|
|
|
|
|
где L - индуктивность контура.
•Индуктивность контура L зависит от формы контура, его размеров и магнитных свойств среды. Индуктивность соленоида: L = µ µ0 n2 lS,
где l - длина соленоида; S - площадь его поперечного сечения; n - число витков на единицу его длины.
ПРИМЕР 3.3. В однородном магнитном поле с индукцией B = 0,05
Тл вращается тонкий однородный стержень длиной l = 20 см так, что ось вращения параллельна линиям индукции и пересекает стержень в точке, удаленной от одного из концов на расстояние, равное ¼ его длины (рис. 3.10). Угловая скорость вращения ω = 20 рад/с. Определить разность потенциалов, возникающую на концах проводника.
РЕШЕНИЕ.
При движении стержня в магнитном поле с ним движутся свободные заряды (электроны), на каждый из них действует сила Лоренца, направленная вдоль проводника, модуль ко-
торой: Fл = qe V Bsin α,
где qe, V - заряд и скорость электрона, соответственно; В - индукция магнитного поля; α - угол между направле-

r |
56 |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ниями векторов скорости V |
и индукции |
B |
|
Х |
|
|
|
|
|
|
|
|
|
|
|
||||
|
r r |
|
|
|
|
|
|
|
|
магнитного поля (в нашем случае V B и |
|
|
r |
|
|
|
|
||
α = 90°, sinα = 1). Под действием этой си- ϕА |
|
|
ω |
|
|
|
r |
||
|
О |
|
|
|
|
||||
лы электроны перемещаются так, что в |
|
|
|
|
|
V |
|||
|
|
|
|
|
|
|
|||
точках А и С создается избыток электро- |
|
|
|
|
|
|
|
||
нов, а в О - их недостаток. Эти заряды соз- |
|
О′ |
|
|
r |
ϕС |
|||
дают кулоновское поле напряженностью |
|
|
|
|
B |
|
|||
|
|
|
|
||||||
r |
|
|
|
|
|
|
|
|
|
E. Со стороны этого поля на электроны |
|
|
Рис. 3.19 |
|
|||||
действует сила, которая противоположна по направлению силе Лоренца
и равна: |
r |
r |
|
Fк = qe E . |
|
При равенстве численных значений этих сил дальнейшее переме- |
||
щение электронов по проводнику прекратится: |
||
|
qe E = qe V B. |
|
Воспользовавшись |
связью |
потенциала ϕ с напряженностью Е, |
можно определить изменение потенциала dϕ на элементарном участке dl длины стержня: dϕ = −E d l.
Учитывая, что E = V B, получим dϕ = −V B d l.
Скорость V электрона на разных расстояниях r от оси вращения стержня связана с угловой скоростью ω вращения: V = ωr .
Тогда разность потенциалов между концами вращающегося стержня:
|
ϕС |
|
|
|
|
|
3l |
|
|
|
|
|
3l |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∫dϕ = − ∫ ωB r d l = −ωB ∫r d l. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
ϕA |
|
|
|
|
− |
l |
|
|
|
− |
l |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Так как l и r берутся вдоль одного направления, то dl=dr. |
|
|
|
|||||||||||||||||||||||||||||||
Тогда |
|
|
|
|
3l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
4 |
|
|
|
9 |
|
|
2 |
|
|
1 |
|
|
2 |
|
|
5 |
|
|
|
2 |
|
||||||||||
ϕС |
−ϕA = −ωB |
|
|
|
|
|
|
|
|
= −ωB |
|
|
|
l |
|
+ |
|
|
|
|
l |
|
= − |
|
|
|
|
ωBl |
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
− |
l |
|
|
32 |
|
|
|
|
|
32 |
|
|
|
|
16 |
|
|
|
|
|
||||||||||
|
|
|
4 |
|
|
|
|
|
|
5 0,05 20 0,04 |
|
|
|
|
|
|
|
|
||||||||||||||||
Произведем вычисления: ϕA −ϕС = |
|
=1,25 В. |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
16 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Проверим размерность: [ϕA −ϕС ]= |
Тл м2 |
|
= |
|
В с м2 |
|
= В. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
м2 с |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
57 |
|
|
|
|
|
|
ПРИМЕЧАНИЯ 3.6: |
|
|
|
|
|
|
|
4. В задаче 3.67 индуктивность L определяется из заданной в ус- |
|
|||||
ловии задачи энергии магнитного поля: |
|
|
|||||
|
|
W = |
L I2 |
. |
|
||
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
5. В задаче 3.66 сечение проводника определяется: |
|
|||||
|
|
S0 = |
πd2 |
, |
|
||
|
|
|
4 |
|
|||
|
|
|
|
|
|
||
где d – диаметр проволоки. Площадь контура S = a2. |
|
||||||
|
6. Возникновение ЭДС само- |
|
I |
|
|
||
индукции сопровождается появле- |
|
I0 |
|
|
|||
нием |
экстратоков |
самоиндукции, |
|
|
1 |
|
|
направление которых определяется |
|
|
|
|
|||
правилом Ленца. При включении |
|
|
|
|
|||
источника тока (задача 3.65) сила |
|
|
2 |
|
|||
тока изменяется по закону |
|
|
|
|
|||
|
|
−R t |
|
|
|
|
t |
|
|
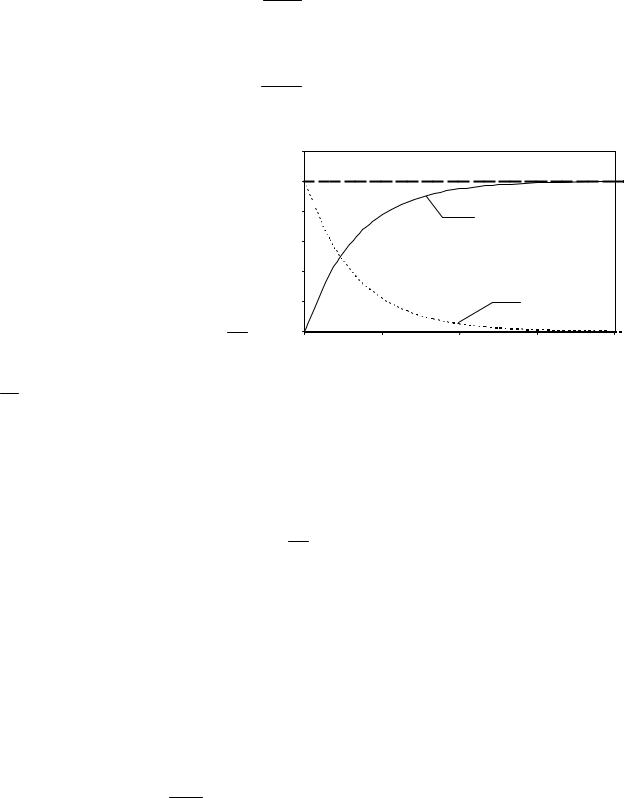
I = I0 (1−e L ), |
|
|
0 |
||
|
|
|
|
Рис. 3.20 |
|||
где I |
= Ε - установившийся ток при t → ∞; L - индуктивность контура; |
|
|||||
|
R |
|
|
|
|
|
|
R - его сопротивление; t - время после замыкания цепи (рис. 3.11, кри- |
|
||||||
вая 1). |
|
|
|
|
|
|
|
|
7. При отключении источника (задача 3.64) сила тока убывает по |
|
|||||
экспоненциальному закону: |
|
|
−R t |
|
|||
|
|
I = I0 e |
|
||||
|
|
L , |
|
||||
|
16. Задачи 3.71-3.80 на тему «Гармонические колебания. |
|
|||||
|
Колебательный контур» [1, гл. 18]; [2, гл. 27]; [3, §6, 26]. |
|
|||||
•Колебания какой-либо физической величины Х называются гар- |
|
||||||
моническими, если их зависимость от времени t имеет вид |
|
||||||
|
|
X = A sin (ωt+ϕ0 ). |
|
||||
•Скорость и ускорение при гармоническом колебании определяют- |
|
||||||
ся уравнениями |
V = d X = ω A cos (ωt+ϕ0 ), |
|
|||||
|
|
|
|||||
|
|
d t |
|
|
|
|
|

58
a = ddVt = −ω2 A sin (ωt+ϕ0 ),
где А – амплитуда колебания; ω - циклическая частота; ϕ0 – начальная фаза.
•Циклическая частота ω, период Т и частота ν связаны соотно-
шениями
ω = 2Тπ = 2 πν .
•Квазиупругая сила, действующая на тело при свободном гармоническом колебании, пропорциональна смещению и направлена в сторону, противоположную смещению (задачи 3.71-3.75):
F = m a = m ω2 X = −k X,
где k = m ω2 - коэффициент квазиупругой силы.
•Полная механическая энергия колеблющейся точки
|
|
E = П+ W = |
k A2 |
, |
||
|
|
|
||||
|
|
k X2 |
2 |
|
||
где |
П = |
- потенциальная энергия; |
||||
2 |
||||||
|
|
|
|
|
||
W = m 2V2 - кинетическая энергия.
•В колебательном контуре, состоящем из конденсатора электроемкостью С и катушки индуктивностью L, возникают электромагнитные колебания, период которых определяется по формуле Томсона
(задачи 3.76 – 3.80):
T = 2 π L C .
•Длина λ электромагнитной волны, на которую резонирует колебательный контур, связана с периодом колебаний Т соотношением
(задачи 3.76 – 3.80)
λ = с T ,
где с = 3 108 м/с - скорость распространения электромагнитных волн в вакууме.
ПРИМЕЧАНИЯ 3.7:
3.В условиях задач 3.71 –3.75 начальная фаза ϕ0 = 0.
4.Скорость и ускорение максимальны при таких значениях аргу-
мента (ωt+ϕ0), при которых cos(ωt + ϕ0 ) = 1, sin(ωt + ϕ0 ) = 1.

59
5. При свободных гармонических колебаниях в контуре (задачи 3.76 –3.79) происходит периодическое преобразование энергии электрического поля Wэл конденсатора в энергию Wм магнитного поля катушки и наоборот. Значения энергии Wэл и Wм изменяются от нуля до максимального значения:
Wmax = C ∆ϕmax2 ,
эл |
|
|
|
2 |
|
||
|
|
||
Wmax = L I2max , |
|||
м |
|
2 |
|
|
|
||
где ∆ϕmax - максимальная разность потенциалов на пластинах конден-
сатора; Imax - максимальное значение силы тока в контуре.
6. Решая задачу 3.77, учтите, что индуктивность катушки (соленоида)
L = µ µ0 N2 S, l
где µ =1, µ0 - магнитная постоянная; S - площадь витка; N - число витков катушки; l - ее длина.
7.При расчете частоты колебаний в контуре в задаче 3.78 найдите предварительно индуктивность и емкость из формулы максимальной энергии электрического и магнитного полей.
8.Определяя диапазон длин волн (задача 3.80), на который настраивается колебательный контур, необходимо в формулу последовательно подставить Сmin и Сmax .
