
Методички / В.М. Андреева Изучение квазистатических электрических полей
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра физики
ИЗУЧЕНИЕ КВАЗИСТАТИЧЕСКИХ ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ
Методические указания к лабораторной работе № 105 для подготовки студентов всех направлений
Составители |
В.М. Андреева |
|
В.В. Дырдин |
|
Г.Б. Исаева |
Утверждены на заседании кафедры
Протокол №5 |
от 3.02.2000 |
Рекомендованы к печати методической Комиссией направления 552900
Протокол №76 |
от 14.03.2000 |
Электронная копия находится в библиотеке главного корпуса КузГТУ.
Кемерово 2000
1
ЛАБОРАТОРНАЯ РАБОТА № 105
ИЗУЧЕНИЕ КВАЗИСТАТИЧЕСКИХ ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ
1. Цели работы: 1. Ознакомление с методами расчета характеристик электрических полей.
2.Освоение экспериментального метода изучения картины расположения эквипотенциальных линий и линий напряженности.
3.Экспериментальная проверка расчетов для модельных полей.
2.Приборы и принадлежности: ванна с электродами различной
формы, частично заполненная водой; источник питания; электронный осциллограф; вольтметр; зонд.
3. Принятые обозначения: жирным курсивом – определения, жирным шрифтом – векторные величины.
4. ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
4.1. Электрическое поле. Напряженность
Вся совокупность электрических и магнитных явлений – это следствие движения и взаимодействия электрических зарядов. Имеется два вида электрических зарядов: положительные и отрицательные. Материальным носителем наименьшего отрицательного заряда является электрон, положительного – протон. Эта наименьшая величина заряда называется элементарным зарядом и равна 1,6 10-19 Кл. Любой электрический заряд кратен элементарному заряду.
Электрические заряды взаимодействуют друг с другом. Причем одноименные заряды отталкиваются, разноименные притягиваются. Сила, с которой взаимодействуют два неподвижных точечных заряда
q1 и q2 в вакууме, определяется по закону Кулона: |
|
|||||
F |
= k |
q1 q2 |
|
r12 |
, |
(4.1) |
|
|
|||||
12 |
|
r122 |
|
r12 |
|
|
|
|
|
|
|||
2
где r12 - радиус–вектор, проведенный из точки расположения заряда q 1
в точку расположения заряда q2; к – коэффициент пропорциональности, зависящий от выбора единиц измерения, входящих в равенство
(4.1). В системе СИ К = 1/(4πε 0) = 9 10 9 |
м/Ф. |
При изменении положения заряда q 2 |
сила F12 будет изменяться |
вобщем случае и по величине, и по направлению. Обычно говорят, что
заряд q 2 находится в поле, созданном зарядом q 1.
Поле, создаваемое неподвижными зарядами, называется электростатическим. Характеристикой его служит вектор, равный силе, действующей на единичный положительный точечный заряд, помещенный
вданную точку пространства. Этот вектор называется напряженно-
стью электрического поля Е.
Е = |
F12 |
= |
1 |
|
|
q1 |
r12 . |
(4.2) |
||
4πε |
|
|
||||||||
|
q |
2 |
|
0 |
|
r |
2 |
r |
|
|
|
|
|
|
|
|
12 |
|
|||
|
|
|
|
|
|
|
12 |
|
|
|
Выражение (4.2) описывает электрическое поле, созданное точечным зарядом q 1 в точке, находящейся на расстоянии r12 от него.
Если поле создается системой точечных зарядов, то для нахождения напряженности результирующего поля используется принцип суперпозиции полей: напряженность поля системы точечных зарядов равна векторной сумме напряженностей полей, создаваемых каждым из точечных зарядов так, как если бы других зарядов не было.
E = ∑ Ei = |
1 |
|
∑ |
|
qi |
ri , |
(4.3) |
4πε |
|
i ri2 |
|||||
i |
0 |
|
ri |
|
|||
где ri - радиус-вектор, проведенный из точки расположения заряда qi
в точку наблюдения.
Если заряд q распределен в пространстве неразрывно так, что его нельзя считать точечным, то условно заряд представляют как систему бесконечно большого числа зарядов dq (q = ∫ dq). Тогда в соответствии с принципом суперпозиции полей напряженность электрического
поля |
|
Е такого заряда |
1 |
|
|
dq |
|
r |
|
|
|
|
|
|
|
Е = ∫ dE = |
|
∫ |
|
, |
(4.4) |
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
4πε |
0 (q) r 2 |
r |
|
|
||||
где |
dq = τ |
dl , если заряд распределен с линейной плотностью τ |
; |
|||||||||
dq = |
σ |
dS , |
если заряд распределен с поверхностной плотностью σ |
; |
||||||||
dq = |
ρ |
dV , |
если заряд распределен с объемной плотностью |
ρ . |
|
|||||||
3
Зная напряженность электрического поля, можно определить силу, действующую на любой точечный заряд, помещенный в данную точку поля:
|
|
|
F = qE. |
|
|
|
|
|
|
|
|
(4.5) |
4.2. Потенциальный характер электростатического поля. |
|
|||||||||||
|
|
|
Потенциал |
|
|
|
|
|
|
|
|
|
|
|
|
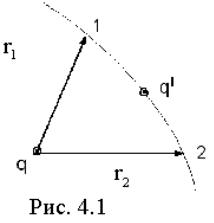
Пусть |
в |
поле, |
|
создаваемом |
|||||
|
|
|
||||||||||
|
|
|
неподвижным |
зарядом q, |
под действием |
|||||||
|
r1 |
|
||||||||||
|
|
кулоновских сил из |
|
точки 1 в точку 2 |
||||||||
|
|
|
перемещается точечный заряд q′. Совер- |
|||||||||
|
|
|
шаемая при этом над зарядом q ′ |
работа |
||||||||
|
|
|
А12 равна: |
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
qq′ |
|
1 |
|
1 |
|
|
|
|
|
A12 = q′ ∫ E d l = |
|
( |
− |
). |
(4.6) |
||||
|
|
|
|
|
|
|
||||||
|
|
|
(1) |
|
|
4πε 0 |
r1 |
r2 |
|
|||
|
|
|
Очевидно, |
что |
работа не |
зависит от |
||||||
|
|
|
||||||||||
формы траектории, по которой перемещается заряд q′, и определяется только радиусами-векторами r1 и r2 начальной и конечной точек
траектории. Этот вывод справедлив и в том случае, когда заряд q′ перемещается в поле, созданном любой системой неподвижных зарядов. Это значит, что электростатическое поле потенциально, и в выбранной системе отсчета потенциальная энергия заряда q′ в данной точке этого поля всегда будет иметь одно и то же значение. Работа потенциальных сил по перемещению заряда q′ из одной точки поля (точка 1) в другую (точка 2) всегда равна убыли потенциальной энергии заряда q′, т.е.
|
|
|
|
|
|
|
|
|
A12 = |
WР1 − |
WР2 , |
|
|
|
|
|
(4.7) |
||||
где WP1 – потенциальная энергия заряда |
q′ |
в точке |
1; WP2 |
– потенци- |
|||||||||||||||||
альная энергия заряда q′ |
в точке 2. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Сравнивая (4.6) |
и (4.7), имеем |
|
|
|
|
|
|
|
qq′ |
|
|||||||||
W |
p |
(r ) = |
1 |
|
qq′ |
; |
W |
p |
(r ) = |
|
1 |
|
qq′ |
|
и |
W |
p |
(r) = |
|
. (4.8) |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
4πε 0 |
|
r1 |
|
2 |
4πε 0 |
r2 |
|
|
|
|
4πε 0r |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Как следует из (4.8), различные по величине заряды q′ в одной и той же точке поля заряда q будут иметь разную потенциальную энергию. Однако величина
4
ϕ (r) = |
WР (r) |
= |
q |
(4.9) |
q′ |
4πε 0r |
от заряда q′ не зависит и может считаться характеристикой данной точки поля заряда q. Эту характеристику назвали потенциалом. Следовательно, потенциал ϕ данной точки поля равен потенциальной энергии, которой обладает единичный точечный заряд в данной точке поля.
Равенство (4.9) дает значение для потенциала поля, создаваемого точечным зарядом q. Если поле создается системой точечных зарядов,
то в соответствии с принципом суперпозиции |
|
ϕ (r) = ∑ ϕ i (r), |
(4.10) |
i |
|
а в случае непрерывно распределенного заряда |
|
ϕ (r) = |
1 |
|
dq |
, |
(4.11) |
||
|
|
|
(q∫) r |
|
|||
|
4πε |
0 |
|
||||
где dq = τ dl, dq = σ dS |
или |
|
dq = |
ρ dV |
в зависимости от харак- |
||
тера распределения заряда.
По определению потенциал электростатического поля является
скалярной функцией координат: |
|
ϕ = ϕ (x, у, z) , |
(4.12) |
поэтому численное значение потенциала всегда определяется с точностью до некоторой постоянной, величина которой зависит от выбора точки с нулевым значением потенциала.
Используя понятие |
потенциала, работу по перемещению заряда q′ |
|
из точки 1 поля в точку |
2 согласно (4.7) и (4.9) |
можно выразить как |
|
A12 = q′(ϕ 1 − ϕ 2 ). |
(4.13) |
4.3. Связь между потенциалом и напряженностью
Электростатическое поле может быть задано двояко: заданием в каждой точке пространства либо вектора (напряженности E ) – силовой характеристики поля, либо скаляра (потенциала ϕ ) – энергетической характеристики поля. Но свойства поля и его характер в каждой точке пространства зависят только от конфигурации системы зарядов и не зависят от способа его написания. Значит, между вектором напряженности E и потенциалом ϕ должна быть универсальная связь. Эту связь можно установить, подсчитав работу по перемещению точечного заряда q′ в электростатическом поле. Согласно (4.13), элементарная работа,
5
совершаемая полем под зарядом q при его перемещении вдоль направления d l , равна
С другой стороны: |
|
|
dA = − q′ dϕ . |
|
|
|
|
(4.14) |
||||||
|
|
dA = |
Fe dl = q′ Ee dl , |
|
|
(4.15) |
||||||||
|
|
|
|
|
|
|||||||||
где |
Fе – проекция силы F на перемещение |
dl . |
|
|
|
|||||||||
|
Сравнивая (4.14) |
и (4.15), получим |
|
|
|
|
|
|||||||
|
|
|
|
|
Ee = − |
dϕ |
, |
|
|
|
|
(4.16) |
||
|
|
|
|
|
|
|
|
|
|
|||||
|
Ее – проекция вектора |
|
|
|
dl |
|
|
|
|
|
||||
где |
E на направлениеl . |
|
|
|
||||||||||
|
Если заряд q′ |
перемещается вдоль оси |
Х (У, Z), то |
|
||||||||||
|
Ex = − |
∂ ϕ |
|
(E |
у = − |
∂ ϕ |
, E z = |
− |
∂ |
ϕ |
) . |
(4.17) |
||
|
∂ x |
|
∂ |
z |
||||||||||
|
|
|
|
∂ у |
|
|
|
|||||||
Символ частной производной означает, что дифференцирование производится только по соответствующей координате.
Вектор напряженности E в декартовой прямоугольной системе координат равен
E = − (еx |
∂ ϕ |
+ еу |
∂ ϕ |
+ еz |
∂ ϕ |
) = − gradϕ . |
(4.18) |
|
∂ x |
∂ у |
∂ z |
||||||
|
|
|
|
|
Выражение в скобках в формуле (4.18) называется градиентом потенциала. Градиент – векторная величина, определяющая быстроту изменения скалярной функции координат по направлению. В данной точке пространства градиент направлен в сторону наиболее быстрого возрастания скалярной функции, а модуль его равен быстроте этого возрастания. Знак минус в выражении (4.18) показывает, что вектор напряженности электрического поля направлен в сторону убывания потенциала. Под действием сил поля положительные заряды движутся в сторону уменьшения потенциала, отрицательные – в сторону возрастания.
4.4. Линии напряженности и поверхности равного потенциала
Для графического изображения электростатического поля используют линии напряженности (силовые линии) и поверхности равного потенциала. Линией напряженности электрического поля называют линию, касательная к которой в каждой точке пространства совпадает с

6
направлением вектора E в этой точке. Густота линий напряженности выбирается так, чтобы число линий, пронизывающих единичную, перпендикулярную к ним площадку, было равно модулю вектора E в данной точке поля. По картине линий напряженности можно судить о направлении и модуле вектора E в разных точках поля.
Силовые линии электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных (либо уходят в бесконечность).
Если в электрическом поле соединить все точки, имеющие одинаковый потенциал ϕ , то получится
поверхность равного потенциала (эквипотенциальная поверхность).
Вектор напряженности электрического поля перпендикулярен в каждой точке эквипотенциальной поверхности и направлен в сторону убывания потенциала. Связь между потенциалом и напряженностью оказывается очень полезной при исследовании электростатических полей. Так, имея картину
линий напряженности поля, можно построить систему эквипотенциальных поверхностей, и, наоборот, зная положение поверхностей равного потенциала, можно построить линии напряженности поля (рис. 4.2). Экспериментально проще изучать распределение потенциала, так как большинство приборов, пригодных для изучения полей, измеряет разности потенциалов, а не напряженности поля.
4.5. Поток вектора напряженности. Теорема Гаусса в электростатике
|
Потоком dФЕ |
вектора E через произвольную площадку назы- |
|
вают скалярное произведение вектора E на вектор dS = |
dS n , |
||
где |
n - единичный положительный вектор нормали к площадке dS: |
||
|
dФЕ = |
Е dS = E dS cos(E, n) = En dS , |
(4.19) |
|
|
|
|
где |
En = E cos (E, |
n) . |
E через по- |
|
Если поверхность S замкнутая, то поток вектора |
||
верхность S равен |
|
|
|

|
7 |
|
|
ФЕ = ∫ dФЕ = |
∫ E dS = |
∫ EndS . |
(4.20) |
(s) |
(s) |
(s) |
|
Вэтом случае в качестве положительной нормали берется внешняя нормаль к поверхности, а сама поверхность называется гауссовой.
Вэлектростатике доказано, что поток вектора напряженности E через произвольную замкнутую поверхность S пропорционален алгебраической сумме зарядов, охватываемых этой поверхностью:
|
|
∑ |
|
qохв |
|
|
|
∫ E dS = |
i |
i |
|
|
|
, |
(4.21) |
||
|
|
|
|||
|
qохв |
(s) |
|
ε 0 |
|
где ∑ |
- алгебраическая сумма зарядов, |
заключенных внутри гаус- |
|||
i |
i |
|
|
|
|
|
|
|
|
|
|
совой поверхности.
Уравнение (4.21) является интегральным относительно E. Решив его, получим значение напряженности Е в точках, принадлежащих гауссовой поверхности. Поэтому равенство (4.21) можно использовать для расчета электростатических полей. На практике применять теорему Гаусса для расчета электрических полей имеет смысл только тогда, когда поле обладает определенной симметрией. Только в этом случае решение интегрального уравнения (4.21) не связано с математическими трудностями.
4.6.Исследование структуры электрических полей
Влабораторной работе рассматривают две задачи.
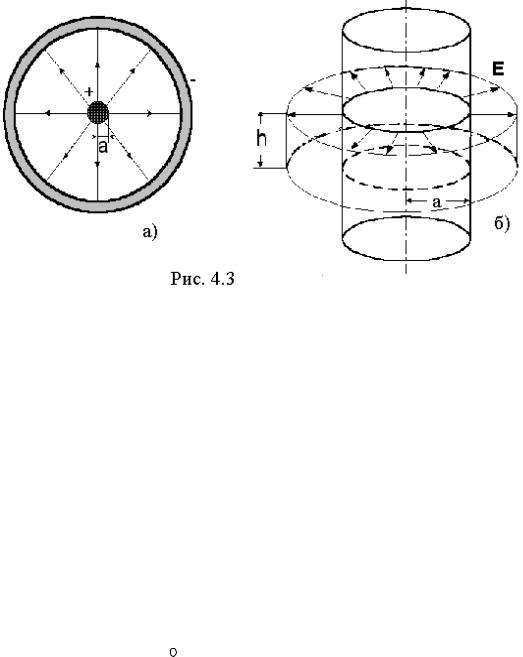
Задача 1. Исследование поля двух коаксиальных бесконечно длинных металлических цилиндров, равномерно заряженных с линейной плотностью τ .
8
Очевидно, что поле цилиндра обладает осевой симметрией. Силовые линии, начинаясь на поверхности металлического цилиндра, уходят в бесконечность по радиусам (рис. 4.3,б). Поэтому поле в этом случае можно рассчитать, используя теорему Гаусса. В качестве гауссовой поверхности целесообразно выбирать цилиндр, коаксиальный с данным, радиусом r, равным расстоянию от оси до точки наблюдения (т. А). Высота h этого цилиндра должна быть такой, чтобы в его пределах не нарушалась симметрия поля.
Поток вектора E через основание выбранного цилиндра равен нулю, так как силовые линии лишь скользят вдоль оснований, не пересекая их. Поток вектора E через гауссову поверхность S будет поэтому равен потоку через боковую поверхность вспомогательного цилиндра:
∫ E dS = |
∫ E dS = E Sбок = E 2π rh . |
(4.22) |
(s) |
(S бок) |
|
Заряд qохв , охватываемый гауссовой поверхностью S, равен :
qохв = τ h . |
(4.23) |
Подставив (4.22) и (4.23) в (4.21), найдем величину напряженности поля на расстоянии r от оси цилиндра:
E 2π rh = τ h / ε 0, |
E = |
ι |
. |
(4.24) |
|
2π rε 0 |
|||||
|
|
|
|
Рассматриваемый заряженный цилиндр – металлический, поэтому все его точки внутри и на поверхности имеют один и тот же потенциал.

|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
Примем его равным нулю (ϕ 0 = 0). Потенциал |
ϕ (r) на расстоянии r |
||||||||||||||
от оси найдем, пользуясь равенством (4.16): |
|
|
|
|
|
|
|||||||||
|
dϕ |
ϕ |
(r) |
|
|
r |
|
ι |
|
r |
dr |
|
|||
Er = − |
|
|
и |
∫ dϕ |
= − |
∫ Er dr = − |
|
|
∫ |
|
, |
||||
dr |
2πε |
|
r |
||||||||||||
откуда |
|
0 |
|
|
a |
|
0 a |
|
|||||||
|
|
|
|
ι |
|
|
r |
|
|
|
|
|
|
|
|
|
|
ϕ |
(r) = − |
|
|
ln |
. |
|
|
|
|
|
(4.25) |
||
|
|
|
2πε |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
a |
|
|
|
|
|
|
||
Как следует из (4.25), |
эквипотенциальные поверхности поля ци- |
||||||||||||||
линдра (а значит, и двух коаксиальных цилиндров) – цилиндрические поверхности, коаксиальные с металлическим цилиндром (рис. 4.4,а).
Если на оси абсцисс откладывать величину ln ar , а на оси ординат
потенциал ϕ (r) (рис. 4.4,б), то на0 графике получится прямая, проходящая через начало координат.
