
Методички / В.В. Дырдин Изучение механических колебаний в упруго связанных системах
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра физики
ИЗУЧЕНИЕ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ В УПРУГО СВЯЗАННЫХ СИСТЕМАХ
Методические указания к лабораторной работе № 212 по курсу общей физики для студентов всех специальностей
Составители В. В. ДЫРДИН Ю. А.ФАДЕЕВ И. С. ЕЛКИН
Утверждены на заседании кафедры Протокол № 6 от 09.02.01 Рекомендованы к печати методической комиссией направления 550600 Протокол № 4 от 27.03.01
Электронная копия находится в библиотеке главного корпуса КузГТУ
Кемерово 2001

1
ЛАБОРАТОРНАЯ РАБОТА № 212
ИЗУЧЕНИЕ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ В УПРУГО СВЯЗАННЫХ СИСТЕМАХ
Данная лабораторная работа относится к разделу «Механические колебания» по теме «Сложение колебаний одного направления».
Перед занятием студент обязан подготовиться к лабораторной работе. На выполнение и защиту данной работы отводится два аудиторных занятия.
1. Цель работы: |
изучить особенности свободных и вы- |
|
нужденных колебаний системы на |
|
примере упруго связанных маятников. |
2.Приборы и принадлежности: установка FPM-13.
3.Подготовка к выполнению. Изучить §§ 27-28 в учебном пособии
[1], гл. IV в [2] и данные методические указания.
4.Теоретическая часть
4.1.Свободные колебания в системе двух упруго связанных маятников
Рассмотрим колебательную систему, состоящую из двух математических маятников, упруго связанных между собой через пружину (рис.1). Два маятника называются упруго связанными, если колебания одного из них передаются другому через невесомую пружину, соединяющую их.
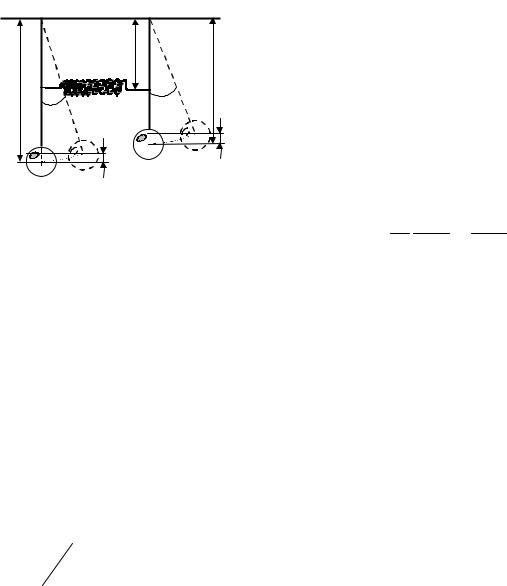
Если углы отклонения маятников от положения устойчивого равновесия малы, то sinϕ ≈ϕ, а cosϕ ≈ 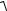 1−ϕ2 ≈ (1−ϕ2 / 2).
1−ϕ2 ≈ (1−ϕ2 / 2).
Из рис.1 видно, что относительное изменение высоты и скорости движения для каждого маятника будет определяться с помощью выражений
|
|
|
hs = ls (1 −cosϕs ) ≈ lsϕs |
2 |
/ 2 ; |
|
|
(1) |
|||||
|
|
|
|
|
vs = |
d |
(ls sinϕs ) ≈ lsϕ&s , где s=1,2. |
|
(2) |
||||
|
|
|
dt |
|
|||||||||
Потенциальная энергия сжатой пружины будет определяться с |
|||||||||||||
помощью выражения |
|
|
|
|
|
|
|
|
|
|
|
||
U пруж. = |
1 |
k∆x2 |
= |
1 |
k(a sinϕ1 −a sinϕ2 )2 |
= |
1 |
ka2 (ϕ1 −ϕ2 )2 |
, |
(3) |
|||
|
|
|
|||||||||||
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|||
2
где ∆x – абсолютное растяжение пружины; k– коэффициент упругости пружины.
Кинетическая и потенциальная энергии системы тогда будут иметь вид
|
|
|
|
|
T = |
1 |
m l 2ϕ&2 + |
1 |
m |
l 2ϕ& |
2 |
; |
|
|
|
(4) |
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 1 |
1 |
2 |
2 |
2 |
|
2 |
|
|
|
|
|
||||
U = |
1 |
m l |
gϕ2 |
+ |
1 |
m |
l |
2 |
gϕ2 + |
1 |
ka2 |
(ϕ |
1 |
−ϕ |
2 |
)2 |
, |
(5) |
|||||||
|
|
|
|||||||||||||||||||||||
|
2 |
1 |
1 |
1 |
|
2 |
|
2 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
где |
m1, m2 – |
массы |
маятников; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
l1 ,l2 – длина первого и второго |
|||
a |
|
маятников, |
соответственно; |
||
|
g = 9,81м/с2; ϕ1 |
,ϕ2 – углы |
от- |
||
l1 |
l2 |
||||
клонения маятников; ϕ&1,ϕ&2 – уг- |
|||||
ϕ1 |
ϕ2 |
||||
ловые скорости маятников. |
|
||||
h |
|
||||
|
Используя |
уравнение |
дви- |
||
h |
m2 |
жения системы – уравнение Ла- |
|||
m1 |
|
гранжа |
|
|
|
Рис.1 |
|
|
|
||
|
d ∂T + ∂U = 0, |
(6) |
|||
|
|
||||
|
|
dt ∂ϕ&s |
∂ϕs |
|
|
получаем систему уравнений |
где s=1,2 , |
|
|
||
|
|
|
|||
m l 2ϕ&& |
+m l |
gϕ |
1 |
−ka2 (ϕ |
2 |
−ϕ |
) = 0; |
(7) |
||
1 1 |
1 |
1 |
1 |
|
|
1 |
|
|
||
m2l22ϕ&&2 |
+m2l2 gϕ2 +ka2 (ϕ2 −ϕ1) = 0. |
(8) |
||||||||
Принимая в (7) |
ϕ2 |
= 0, что соответствует случаю, когда второй |
||||||||
маятник закреплен, перейдем к уравнению, решая которое получим выражение для первой так называемой парциальной частоты ωр1
ω2p |
|
= |
g |
+ |
ka2 |
, |
(9) |
|
1 |
l1 |
m l 2 |
||||||
|
|
|
|
|
||||
|
|
|
|
1 1 |
|
|
||
где ω021 = g l1 – квадрат собственной частоты первого маятника.
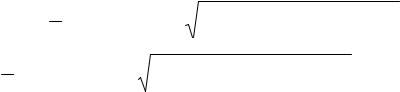
Из (8) при ϕ1 = 0 получим выражение для второй парциальной частоты
ω2p |
|
= |
g |
+ |
ka2 |
. |
(10) |
|
|
|
|||||
|
2 |
|
l2 m2l22 |
|
|||
3
Введем коэффициенты, характеризующие упругую связь маятни-
ков:
|
|
|
|
|
|
|
|
α |
1 |
|
|
= |
ka 2 |
|
; |
|
|
|
|
|
|
|
|
|
(11) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m l 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
2 |
|
= |
ka 2 |
. |
|
|
|
|
|
|
|
|
(12) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2l |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставляя (9) и (10) в (7) и (8), получаем систему двух линейных |
||||||||||||||||||||||||||||||||
дифференциальных уравнений второго порядка |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
−α1ϕ2 = 0 |
|
|
|
|
|
|
|
|
|||||||||||
ϕ&&1 +ωp1ϕ1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
ϕ&& +ω2 |
|
ϕ |
|
|
|
−α |
2 |
ϕ |
1 |
= 0 . |
|
|
|
|
|
|
(13) |
|||||||||||||||
|
2 |
|
|
|
|
p |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ее решение будем искать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
ϕ1 = Acos(ω1t +φ0 ) ; |
|
|
|
|
|
|
(14) |
||||||||||||||||||||||||
|
ϕ2 |
= B cos(ω2t +φ0 ). |
|
|
|
|
|
(15) |
||||||||||||||||||||||||
Подставляя (14) и (15) в (13), находим |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
A |
−α1B = 0 |
|
|
|
|
|
|
|
||||||||||||
−ω1 |
|
A +ωp |
1 |
|
. |
|
|
|
|
(16) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2p |
|
|
|
|
|
|
|
2 A = |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
−ω22 B |
+ω |
2 |
B |
−α |
0 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда получаем уравнение для определения частот |
|
|||||||||||||||||||||||||||||||
ω4 −ω |
2 (ω |
2 |
|
+ω |
|
2 |
2 |
) +ω |
2 |
ω2 |
2 |
−α α |
|
= 0 . |
(17) |
|||||||||||||||||
|
|
|
p1 |
|
|
|
|
|
p |
|
|
|
|
|
p1 |
p |
|
|
|
1 2 |
|
|
||||||||||
Решение этого биквадратного уравнения дает две возможные час- |
||||||||||||||||||||||||||||||||
тоты колебаний системы ω1 |
|
и ω2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)2 + 4α1α2 ];(18) |
||||||||||
ω12 = |
|
1 |
[ω2p |
1 |
|
+ω |
2p |
2 |
− |
|
(ω2p |
1 |
|
−ω2p |
2 |
|||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ω22 = 1 |
[ω2p |
1 |
|
+ω2p |
2 |
|
+ |
|
(ω |
|
2p |
1 |
−ω |
2p |
2 |
)2 + 4α1α2 ]. |
(19) |
|||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Частоты ω1 и ω2 называются собственными или нормальными.
Из выражений (18) и (19) видно, что они не равны парциальным частотам ωp1 и ωp 2 . Данные частоты системы зависят от коэффициента
связи. Если маятники идентичны, то последние выражения упрощают-
ся. При l1=l2 , m1=m2 и α1 =α2 справедливо |
|
ω1,22 = ω2p ±α . |
(20) |
Величина α определяет передачу энергии от одного маятника к другому. Если взаимодействие между маятниками мало, то передача
4
энергии все-таки происходит. Однако этот процесс длится значительно
дольше, чем при сильном взаимодействии. |
|
|
и ωp |
|
|
|
уравнения колеба- |
|||||||||||
При равенстве парциальных частот ωp |
1 |
2 |
|
|||||||||||||||
ний для обоих маятников будут иметь вид |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
ϕ1 |
= ϕ0 cos |
(ω2 −ω1 )t |
cos |
(ω2 +ω1 )t |
|
; |
(21) |
||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
ϕ2 |
= ϕ0 χ sin |
(ω2 −ω1 )t |
sin |
(ω2 +ω1 )t |
|
, |
(22) |
||||||||
|
|
|
|
|
|
|||||||||||||
|
ω2 |
−ω2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где χ = |
p |
|
|
– коэффициент распределения амплитуд. |
|
|||||||||||||
|
α |
|
|
|||||||||||||||
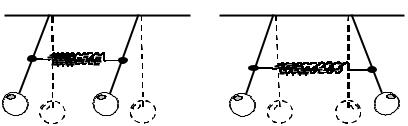
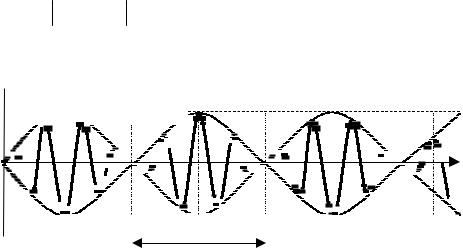
Коэффициент распределения амплитуд χ при идентичных маят-
никах принимает два значения 1 и -1, а колебания при этом будут синфазные (рис.2,а) и противофазные (рис.2,б), соответственно. В первом случае, разность фаз кратна ± 2πn , а во втором случае – ±(2n +1)π , где
n– целое число.
а) |
б) |
|
Рис.2 |
4.2. Биения
Предположим, что маятники могут совершать колебания только в одной плоскости, т.е. имеют одну степень свободы. В этом случае при различных частотах уравнения колебаний для двух упруго связанных
маятников можно записать в виде: |
|
|
|
А1= А01 |
sin(ω1 |
t + φ1); |
(23) |
A2= A02 |
sin(ω2 |
t + φ2), |
(24) |
где А01 и А02 – амплитуды колебаний первого и второго маятников, соответственно; φ1 и φ2 – начальные фазы первого и второго маятников, соответственно.
Результатом сложения может оказаться апериодический процесс, если частоты ω1 и ω2 не соизмеримы между собой. Если же частоты
5
соизмеримы между собой, тогда можно найти такую частоту ω0, что выполняются соотношения
ω1= m ω0; |
(25) |
ω2= n ω0, |
(26) |
где m и n – целые числа. |
|
В простейшем случае, когда А01=А02=А0, уравнение |
результи- |
рующего колебания, полученное путем сложения двух начальных при использовании правила сложения синусов, будет иметь вид
А= А1 + А2 = А0 (sin(mω0t +φ1 ) + sin(nω0t +φ2 )) =
|
|
|
|
|
|
|
m − n |
|
|
|
φ |
−φ |
2 |
|
m + n |
|
|
φ |
+φ |
2 |
|
|
||||||
|
|
= 2A |
cos |
|
|
|
|
ω |
|
t + |
1 |
|
sin |
|
ω |
|
t + |
1 |
|
. |
(27) |
|||||||
|
|
|
|
2 |
|
|
2 |
|
2 |
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
||||
|
Из |
|
последнего |
|
|
выражения |
|
видно, |
|
что |
|
|
множитель |
|||||||||||||||
|
m − n |
|
|
|
φ |
2 |
−φ |
|
|
|
представляет |
собой |
|
амплитуду |
результи- |
|||||||||||||
2A |
cos |
|
|
ω |
|
t + |
|
1 |
|
|
|
|
||||||||||||||||
2 |
|
|
|
|
2 |
|
|
|
||||||||||||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рующего колебания, зависящую от времени и изменяющуюся с частотой (ω1 −ω2 ) / 2 , а (ω1 +ω2 ) / 2 – частота результирующего колебания.
В случае, если ω1 и ω2 близки по абсолютной величине, при этом ∆ω<< ω1, ω2, где ∆ω = ω1 −ω2 , тогда результирующее колебание будет
иметь вид, представленный на рис.3.
А
2А0


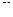





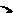


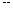






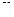



0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
–2А0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tδ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Как видно из рис. 3, амплитуда результирующего колебания является функцией времени. Такие колебания называются биениями, а час-
тота ωδ =(ω1–ω2) называется циклической частотой биения. |
|
||||
Период биений определяется соотношением |
|
||||
T = |
2π |
|
|
. |
(28) |
(ω −ω |
|
) |
|||
δ |
2 |
|
|
||
|
1 |
|
|
|
|

6
4.3.Вынужденные колебания
Вреальных системах колебания затухают, а пополнять потерю энергии можно за счет периодического воздействия внешней силы.
Пусть на стержень одного из связанных маятников действует внешняя сила F, изменяющаяся по гармоническому закону:
F = F0 cosωВt. |
(29) |
После приложения силы F к стержню маятника возникает переходной режим вынужденных колебаний. При этом каждый из маятников одновременно участвует в двух колебаниях, одно из которых сво-
бодное с частотой: ω1 = ω02 − β 2 , где β = 2bm - коэффициент затухания,
b – коэффициент сопротивления среды, будет затухать. Амплитуда колебания достаточно быстро уменьшается, а уравнение колебания описывается выражением:
А1=А01·е-βt·sin (ω1t + φ0). |
(30) |
Другое колебание соответствует незатухающим гармоническим колебаниям с частотой вынуждающей силы.
Амплитуды колебаний зависят от частоты вынуждающей силы ωВ, и при ωВ =ω0 будет наблюдаться первый резонанс. При этом маятники совершают синфазные колебания (рис.2,а). Повышая частоту вынуждающей силы ωВ далее, получим второй резонанс, но маятники при этом будут совершать противофазные колебания (рис.2,б).
5. Описание лабораторной установки
Общий вид лабораторной установки FPM-13 для выполнения данной лабораторной работы представлен на рис.4.
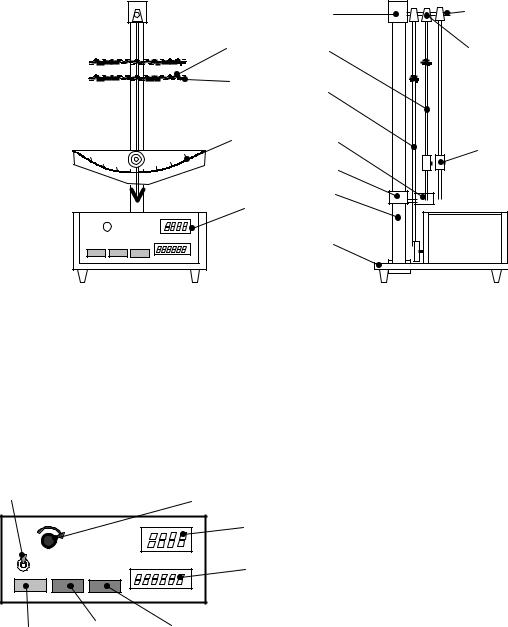
На основании 1 закреплена колонка 2, на которой закреплены втулка 3 и кронштейн 4. На стержне 5 втулки находится три подвески 6, на которых крепятся два маятника 8 и стержень 7, посредством которого возбуждаются колебания. Маятники 8 состоят из стержня и перемещаемого груза 9. Маятники упруго связаны между собой при помощи двух пружин 10, закрепленных в скобообразной обойме 11, которую можно перемещать вдоль стержней маятников. Возбуждение колебаний осуществляется при помощи приводного диска, закрепленного на вале электродвигателя. Диск двигает стержень 7, связанный двумя пружинами 10 со стержнем одного из маятников, и тем самым
7
вызывает его колебания. Электродвигатель находится в блоке управления и измерений 12.
|
|
3 |
6 |
10 |
|
8 |
5 |
11 |
|
7 |
|
|
|
|
|
13 |
|
14 |
9 |
|
|
4 |
|
|
|
|
|
12 |
2 |
|
|
|
|
||
|
|
1 |
|
|
Рис.4 |
|
|
Угловая амплитуда колебаний маятников определяется с помощью шкалы 13. К нижнему кронштейну прикреплен фотоэлектрический датчик 14, с помощью которого определяется число полных колебаний.
Лицевая панель блока управления 12 представлена на рис. 5. включение двигателя регулятор частоты двигателя
“сеть” “сброс” “стоп” |
индикация числа полных колебаний индикация времени колебаний
Рис. 5 Включение установки осуществляется кнопкой “сеть”. Кнопкой
“стоп” ограничивается число полных колебаний. Нажатием клавиши “сброс” блок подготавливается к новому измерению.
6.Выполнение работы
6.1.Подготовить прибор к измерениям. Для этого необходимо сделать следующее:
-подключить прибор к питающей сети;
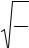
8
-установить одинаковые грузы m1=m2=m на обоих маятниках, на одном и том же расстоянии от оси колебаний;
-нажать клавишу “сеть” и проверить свечение лампочки фотоэлектрического датчика и индикаторов измерителя;
-включить питание двигателя и, плавно вращая ручку регулятора частоты, проверить, работает ли двигатель и колеблется ли маятник.
6.2.Измерить собственную частоту колебаний маятника.
Для этого необходимо отсоединить от маятника пружины, соединяющие его с другим маятником и приводным механизмом. Один из них отклонить на угол 6-100 и отпустить его. После чего нажать клавишу “сброс” и после подсчета прибором 10 полных колебаний маятника нажать кнопку “стоп”. Показания индикаторов занести в табл. 1. Измерения провести пять раз. Найти частоту собственных колебаний
маятника по формуле ω |
0 |
= |
2πn |
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число |
|
|
|
|
|
|
Частота |
Расчетная |
|
|
Погрешность |
|
|
|
№ |
|
полных |
Время |
|
|
собственных |
|
|
|
||||||
|
|
колебаний |
t, с |
|
|
колебаний ω0, |
частота |
|
|
измерений |
|
|||||
|
|
|
|
|
-1 |
|
|
|
|
|
||||||
|
|
|
n |
|
|
|
|
|
|
с-1 |
ω0теор, с |
|
|
|
ε, % |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравнить ее с результатами расчета по формуле ω |
0 |
теор |
= g . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Приборная погрешность измерения времени составляет 0,02 %.
6.3. Определение частот синфазных и противофазных колеба-
ний.
Для этого необходимо сделать следующее:
-присоединить пружины, осуществляющие упругую связь между маятниками;
-отклонить маятники в одну сторону на угол 6-100, отпустить их, аналогично пункту 6.2 измерить частоту синфазных колебаний
ωс;
-измерения провести 5 раз, данные занести в табл. 2;
-оценить погрешность измерений по теории погрешностей;
9
-отклонить маятники в противоположные стороны на одинаковый угол 100 и отпустить их;
-измерить частоту противофазных колебаний ωп. Данные занести в табл. 2;
-оценить погрешность измерений.
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частота синфазных |
|
|
Частота противофазных |
||||||||
|
|
колебаний |
|
|
|
колебаний |
|
|
|
|||
№ |
n |
t, с |
ωс, |
|
ε, % |
№ |
n |
t, с |
ωп, |
|
ε, % |
|
с-1 |
|
с-1 |
|
|
||||||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
|
5 |
|
|
|
|
|
5 |
|
|
|
|
|
|
6.4. Определение частоты колебаний маятника при наличии упругой связи маятника.
- закрепить неподвижно один маятник, придержать его рукой, например, а другой отклонить на угол 7-100 и определить частоту его ко-
лебаний ωp ;
-провести пять измерений, данные занести втабл. 3;
-рассчитать коэффициент упругойсвязи по формуле
αэкс = ω2p −ω02 ;
- сравнить рассчитанные результаты со значением коэффициента αтеор, найденным по формуле (11), где k=11,02 Н/м.
Таблица 3
|
Частота колебаний маятника |
Коэффициент |
Коэффициент |
ε, |
||||
|
упругой связи |
упругой связи |
||||||
|
при наличии упругой связи |
(экс.знач.) |
(теор.знач.) |
% |
||||
|
|
|
|
|
|
|||
|
№ |
n |
t, с |
|
ωр , с-1 |
αэкс, с-2 |
αтеор , с-2 |
|
|
1 |
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
6.5. Определение частот при биениях. Для этого необходимо |
||||||
выполнить следующее: |
|
|
|
|
||||
|
|
- отклонить один из маятников на угол 8-120, другой придержать |
||||||
рукой в положении равновесия. Одновременно отпустить оба маятника и наблюдать колебательный процесс, называемый биениями;
