Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

Физика

Файл:

Методички / А.А. Колесникова Изучение поступательного и вращательного движения с помощью маятника Обербека

.pdf

Скачиваний:

Добавлен:

19.08.2013

Размер:

297.74 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение высшего профессионального образования

«КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра физики

ИЗУЧЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА

Методические указания к изучению темы «Кинематика и динамика поступательного и вращательного движения» и выполнению лабораторной работы № 220 по курсу общей физики

для подготовки студентов всех направлений

Составители А.А. Колесникова Л.Г. Соколова С.Ю. Мартьянова

Утверждены на заседании кафедры Протокол № 6 от 03.03.03

Рекомендованы к печати методической комиссией направления 550600 Протокол № 3 от 11.03.03 Электронная копия находится в библиотеке главного корпуса ГУ КузГТУ

Кемерово 2003

ЛАБОРАТОРНАЯ РАБОТА № 220

1. Цель работы: а) изучить законы поступательного и вращательного движения тел;

б) определить экспериментально кинематические и динамические характеристики поступательного и вращательного движений тел; в) проверить основной закон динамики враща-

тельного движения.

2.Оборудование: установка типа РРМ-06 с маятником Обербека.

3.Подготовка к работе: а) изучить необходимые теоретические

положения по учебникам [1] (гл. 1, 2, 4) и [2] (гл. 1, 2, 4);

б) ответить на контрольные вопросы.

4.Теоретическая часть

Вмеханике используются некоторые модельные представления – материальная точка, абсолютно твердое тело и т. д.

Абсолютно твердое тело – это тело, размеры и форма которого в процессе движения не изменяются.

Вдальнейшем материальную точку и абсолютно твердое тело будем называть терминами «точка» и «тело».

Движение тел подразделяют на поступательное и вращательное. Поступательное движение – это такое движение тела, при кото-

ром любая прямая, мысленно проведенная на теле, остается все время параллельной самой себе.

Вращательное движение – это движение, при котором все точки тела описывают окружности; центры окружностей лежат на одной прямой, называемой осью вращения.

4.1.Кинематические характеристики поступательного движения тела

Любое твердое тело состоит из множества материальных точек. При поступательном движении тела все его точки движутся по одинаковым траекториям, за одно и то же время проходят одинаковые пути и, следовательно, имеют одинаковые скорости и ускорения. Поэтому движение тела может быть описано с помощью характеристик и урав-

нений движения какой-либо одной точки, выбранной на теле. В качестве такой точки может быть использован центр масс тел.

Кинематическими характеристиками движения точки являются:

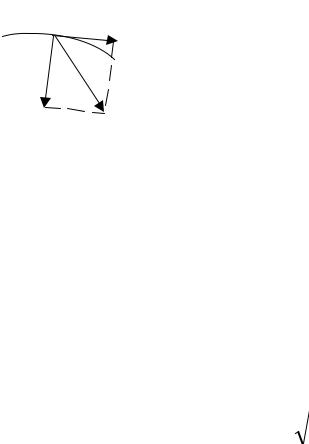
1)вектор перемещения ∆ r – это вектор, соединяющий начальную А и конечную В точки движения (рис. 1);

2)пройденный путь ∆s – это длина траектории между точками А и В (рис. 1); если движение прямолинейное, то модуль вектора перемещения равен пройденному пути:

				∆r	= ∆s ;
	∆s			∆r	= ∆s ;
		3) вектор средней			скорости	< vr >, равный
		3) вектор средней			скорости	< vr >, равный
		перемещению точки за единицу времени:
Рис. 1				< vr >= ∆r ;
				< vr >= ∆r ;		(1)
					∆t
4) средняя путевая скорость < v > – это величина, равная пути,
пройденному точкой за единицу времени:
		< v >=	∆s ;			(2)
			∆t
5) среднее ускорение точки < a > – это изменение скорости за
единицу времени:			∆v ;
		< ar >=	∆v ;			(3)
			∆t

6) вектор мгновенной скорости v – это производная радиуса-

вектора по времени:

vr = lim		∆r		=	dr	;	(4)
		∆t			dt
∆t→0
7) мгновенная путевая скорость v						– это производная пути по
времени:	∆s		ds
v = lim		=					(5)
	∆t
∆t→0				dt ;

8) мгновенное ускорение a – это производная скорости по времени:

av = lim	∆v	=	dv	.	(6)
	∆t
∆t →0			dt

В случае криволинейного переменного движения мгновенное ус-

корение равно геометрической сумме нормального an

и тангенциаль-

ного aτ ускорений (рис. 2):

a =an + aτ .

(7)

aτ

a τ

Нормальное an (центростремительное) ус-

корение характеризует быстроту изменения ско-

arn

рости по направлению. Вектор arn направлен по

Рис. 2

радиусу к центру кривизны траектории и рассчи-

тывается по формуле

an =

(8)

Тангенциальное aτ (касательное) ускорение характеризует бы-

строту изменения скорости по величине. Направлено arτ

по касатель-

ной к траектории движения и рассчитывается по формуле

aτ

(9)

Модуль полного ускорения рассчитывается по теореме Пифагора:


a = an		2 + aτ		2 .	(10)

4.2. Кинематические характеристики вращательного движения тела

Вращательное движение тела, как и поступательное, можно описать, изучая движение одной точки, так как при вращательном движении все точки тела движутся по окружностям, радиусы которых за одно и то же время поворачиваются на один и тот же угол ∆ϕ , имеют одинаковые угловую скорость w и угловое ускорение ε .

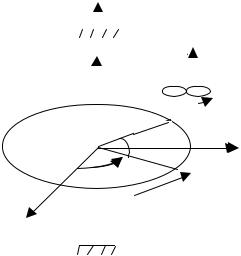
1) угол поворота ∆ϕ (угловое перемещение) равен отношению длины дуги ∆s к радиусу окружности ∆ϕ = ∆s / r (рис. 3) и измеряется в радианах (рад). Ориентация плоскости окружности в пространстве задается единичным вектором нормали n к этой плоскости:

∆ϕ = ∆ϕn .

(11)

Направление вектора ∆ϕ , как

и n , определяется по правилу бу-

равчика.

2) средняя угловая скорость < wr >

n∆

–

величина, характеризующая быстроту враще-

∆ϕ

ния радиуса точки и равная углу поворота его

за единицу времени:

∆ϕ

;

(12)

∆ϕ

∆S

< w >=

∆t

∆S

ϕ0

3) мгновенная угловая скорость

w –

величина, равная производной угла поворота

радиуса точки по времени:

∆ϕ

dϕ

(13)

w = ∆limt →0 ∆t

Рис. 3

Направлениеr вектора угловой скорости w совпадает с направлением нормали n (wr ↑↑ nr). Размерность угловой скорости [w] = 1рад/с=с–1.

4) среднее угловое ускорение <ε > – величина, характеризую-

щая быстроту изменения угловой скорости ∆w за конечный промежуток времени ∆t :

< εr >=

∆w

;

(14)

∆t

5) мгновенное угловое ускорение ε

– величина, равная произ-

водной угловой скорости по времени:

∆w =

εr = lim

(14-а)

∆t→0

∆t

Вектор углового ускорения ε сонаправлен с вектором прираще-

ния угловой скорости dw

(ε

↑↑ dw), поэтому при ускоренном вращении

εr

↑↑ wr

; при замедленном вращении dw

0, вектор углового ус-

корения противоположен вектору угловой скорости, εr ↑↓ wr .

4.3.Кинематические уравнения движения точки

ипоступательного движения тела

Описание движения точки сводится к нахождению ее радиуса-
вектора rr	или трех координат x, y, z		как функций времени:
	rr = rr(t) ,	x = x(t) ,	y = y(t) ,	z = z(t) ,	(15)

а также к нахождению вектора мгновенной скорости vr или его проекций на координатные оси как функции времени:

v = v(t),

vx =vx (t),

v y = v y ( t ),

vz = vz ( t ).

(16)

Конкретный вид этих уравнений зависит от характера движения.

4.3.1. Равномерное прямолинейное движение

Равномерным называется движение с постоянной по величине скоростью, vr = const , следовательно, тангенциальное ускорение точки

равно нулю, aτ = 0 . Для прямолинейного движения характерно посто-

янство направления движения, v = const . При этом радиус кривизны траектории стремится к бесконечности и, как видно из формулы (8), нормальное ускорение равно нулю, an = 0 .

Направим ось x по направлению движения точки, тогда уравнение (5) в проекции на эту ось примет вид:

vx = dxdt ,

откуда dx = vxdt, где dx – элементарно малое приращение координаты точки за элементарно малый промежуток времени dt; vx – мгновенная скорость точки. Значение координаты через промежуток времени t найдем как интеграл от dx:

x = ∫dx = ∫v x dt + c = v x t + c ,

где с – постоянная интегрирования, значение которой находится из начальных условий: при t = 0 x0 = c. Формула для координаты принимает

вид:

x = x0 +vx t .

(17)

Пройденный путь в этом случае находится как разность коорди-

нат:

s= x(t2 ) − x(t1) = vx ∆t .

4.3.2.Равноускоренное прямолинейное движение

При равноускоренном прямолинейном движении vx ≠ const , aτ ≠ 0 , an = 0 , a = aτ .

Формулу (6) запишем в виде:

dvx =axdt .

Мгновенное значение скорости равно интегралу от dvx:

v x = ∫ax dt +c = v0 x +ax t .					(18)
Постоянная интегрирования с равна v0x, что следует из началь-
ных условий: при t0 = 0, с = v0x.
Уравнение для координаты x принимает вид:
x = ∫v x dt +c = ∫(v0 x +ax t )dt +c .
После интегрирования получаем:			t 2
x = x0 +v0 x t +	a	x	t 2		(19)
		x		.
		2		.
		2
Постоянная с здесь имеет смысл начальной координаты					с = x0
(при t0 = 0).

4.4. Кинематические уравнения вращательного движения

Эти уравнения представляют собой зависимость от времени угловых характеристик:

ϕ =ϕ(t) ,

w = w(t) .

(20)

Используя формулы (13) и (14) и следуя схеме рассуждений разделов 4.3.1. и 4.3.2., получим уравнения:

а) для равномерного вращательного движения:

w =const ,

ε =0,

ϕ =ϕ0 +wt ;

(21)

б) для равноускоренного вращательного движения:

ε = const , w = w0 +εt , ϕ =ϕ0 + w0t +	εt 2	. (22)
	2

Связь между линейными и угловыми характеристиками выражается формулами:

v = wr ,

aτ =εr ,

∆s = ∆ϕr .

(23)

4.5. Динамические характеристики и законы поступательного движения

К динамическим характеристикам поступательного движения тела (точки) относятся:

а) масса тела m – мера инертности тела;

	7
б) сила Fr – мера взаимодействия тел;
в) импульс тела	Pr – произведение массы тела на его скорость
( P = mvr );
г) кинетическая	энергия Ек – энергия движущегося тела
(Ек = mv2 / 2);

д) потенциальная энергия Еп – энергия тела в силовом поле или

энергия взаимодействия тел. Для каждого вида взаимодействия формула потенциальной энергии имеет свой вид. Так, при гравитационном взаимодействии тел массой m1 и m2 потенциальная энергия равна:

Еп = G m1rm2 + c,

где G – гравитационная постоянная; r – расстояние между центрами масс тел; с – постоянная величина, с точностью до которой определяется потенциальная энергия. При соответствующем выборе начала отсчета для Еп постоянную с можно положить равной нулю. Если за начало

отсчета потенциальной энергии тела массой m в гравитационном поле Земли принять поверхность Земли, то на высоте h от поверхности

Еп = mgh.

Потенциальная энергия упруго деформированного тела равна:

Еп = кx22 ,

где к – коэффициент упругости тела; х – величина деформации.

е) механическая работа А – величина, равная интегралу от ска-

лярного произведения векторов силы F и перемещения drr:

A = ∫Fdrr =∫Fdr cosα ,

где α – угол между векторами F и dr .

Если сила постоянна по величине и направлению, а движение прямолинейное, то работу силы можно считать по формуле

A = Fs cosα ,

где s – путь, пройденный телом под действием силы.

Основным законом динамики поступательного движения тела является второй закон Ньютона: ускорение тела прямо пропорционально геометрической сумме сил, приложенных к телу, и обратно пропорционально его массе:

	n	r
ar =	∑Fi			n	r
	i=1			n	r
	i=1		,	∑Fi = mar.		(24)
	m		,	∑Fi = mar.		(24)
	m			i =1

Выражение ∑n Fri = mar называют основным уравнением динамики

i =1

поступательного движения.

Одним из фундаментальных законов физики является закон сохранения механической энергии: в замкнутой консервативной системе тел полная механическая энергия сохраняется неизменной, т. е. не изменяется со временем:

Eп + Eк = const .

(25)

Если в системе действуют и неконсервативные силы (сила трения), то изменение механической энергии равно работе неконсервативных сил:

∆E = Aнеконс.

(26)

4.6. Динамические характеристики и законы вращательного движения тела

4.6.1. Момент инерции J

Величина, являющаяся мерой инертности тела при вращательном движении, называется моментом инерции тела относительно оси вращения.

Момент инерции материальной точки относительно оси вращения равен произведению массы этой точки на квадрат расстояния от оси:

J = mr 2 .

(27)

Момент инерции тела относительно оси вращения равен сумме моментов инерции точек, из которых состоит это тело:

J = ∑mi ri 2 .

i=1

Расчет момента инерции однородных тел правильной геометрической формы производится интегрированием по всему объему V тела:

J = ∫ρr 2dV .	(28)
V

Момент инерции некоторых тел:

а) диска и сплошного цилиндра относительно оси, проходящей через центр инерции и перпендикулярной плоскости диска или основанию цилиндра:

J =	1	mR 2	,	(29)
	2

где m – масса диска или цилиндра; R – радиус диска или основания цилиндра;

б) тонкого обруча и тонкостенного цилиндра относительно оси, перпендикулярной плоскости кольца или основанию цилиндра и проходящей через центр масс или через центр инерции цилиндра:

J = mR2 ;			(30)
в) тонкого длинного стержня длиной l относительно оси, перпен-
дикулярной стержню и проходящей через центр масс стержня:
J =	1	ml 2 .	(31)

12

Расчет момента инерции J относительно произвольной оси производится с помощью теоремы Штейнера:

J = J0 +md 2 ,

(32)

где J0 – момент инерции тела относительно оси, параллельной данной и

проходящей через центр масс тела; m – масса тела; d – расстояние между осями.

Размерность момента инерции [J] = 1 кгм2.

4.6.2. Момент силы M

Изменение состояния вращения тела зависит не только от величины силы F , но и от способа ее приложения. Пусть к некоторому телу в

точке А приложена сила F (рис. 4).

Моментом силы относительно точки (центра) О называется векторное произведение радиуса-вектора r точки приложения силы на

вектор силы F :

M = [rrF ].	(33)
Модуль вектора M равен:
M = Fr sin α ,	(34)

1 / 31 2 3 > Следующая >>>

Соседние файлы в папке Методички