
Методички / Г.Б. Исаева Изучение спектра атома водорода и определение постоянной Ридберга
.pdfМинистерство образования Российской Федерации Государственное учреждение Кузбасский государственный технический университет
Кафедра физики
ИЗУЧЕНИЕ СПЕКТРА АТОМА ВОДОРОДА И ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА
Методические указания к лабораторной работе № 88 по курсу общей физики для студентов всех направлений подготовки
Составители |
Г.Б. Исаева |
|
Т.А. Балашова |
Утверждено на заседании кафедры Протокол № 3 от 13.11.01
Рекомендовано к печати методической комиссией направления 550600 Протокол № 8 от 04.12.01
Электронная копия находится в библиотеке главного корпуса ГУ КузГТУ
Кемерово 2002
1
ЛАБОРАТОРНАЯ РАБОТА № 88 ИЗУЧЕНИЕ СПЕКТРА АТОМА ВОДОРОДА
ИОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА
1.Приборы и принадлежности: спектрометр, ртутная и водородная лампы, их источники питания, атлас спектральных линий.
2.Цель работы: изучение спектральной закономерности в спектре атома водорода, определение спектроскопическим методом постоянной Ридберга, потенциала ионизации атома водорода.
3.Подготовка к работе: ознакомиться с описанием лабораторной
работы, изучить в [1] §§ 209, 210, 223, 225 и в [2] §§ 38.2 – 38.4, 39.1, 39.4.
4. Теоретические положения
Атом водорода 11 Н является простейшей атомной системой. В центральном поле ядра – протона – движется один электрон. Так как масса протона примерно в 1840 раз больше массы электрона, то в первом приближении ядро можно считать неподвижным силовым
центром и потенциальную энергию электрона равной
U (r)= − ke2 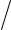 r,
r,
где k = 9 109 м/Ф; заряд электрона e = 1,6 10-19 Кл; r – расстояние между электроном и ядром. Стационарное уравнение Шредингера для электрона в этом поле имеет вид
∆Ψ + |
2me |
(E −U (r))Ψ = 0, |
(1) |
2 |
|||
|
h |
|
|
где me = 9,1 10-31 кг – масса электрона; ħ = h/2π - естественная единица момента импульса (h = 6,626 10-34 Дж с – постоянная Планка); Е – полная механическая энергия электрона; Ψ = Ψ(rr) – волновая функция, описывающая состояние системы.
Поскольку потенциальная энергия U(r) — центральносимметричная функция r, уравнение (1) удобнее решать в сферических координатах r, ϑ, ϕ. Физическим смыслом обладают решения, удовлетворяющие стандартным условиям: это – однозначные, конечные
и непрерывные функции во всей области изменения координат:
0 ≤ r ≤ ∞, 0 ≤ϑ ≤π, 0 ≤ϕ ≤ 2π.

|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
В сферических координатах уравнение (1) имеет вид |
|
|
||||||||||||||
1 |
|
∂ |
∂ψ |
|
1 |
|
∂ |
∂ψ |
|
1 |
∂2ψ |
|
2m |
e2 |
|
|
|||
|
|
|
r2 |
|
+ |
|
|
|
sinϑ |
|
+ |
|
|
+ |
e |
(E+k |
|
)ψ=0. |
(2) |
|
|
|
|
|
r2 sin2 ϑ∂ϕ2 |
|
r |
||||||||||||
r2 ∂r |
∂r |
|
r2 sinϑ∂ϑ |
∂ϑ |
|
|
h2 |
|
|
||||||||||
Решение уравнения (2) зависит от знака полной энергии Е. Случай, когда Е > 0, соответствует свободному электрону, Е < 0 – электрону, связанному с ядром, причем набор собственных значений
энергии, соответствующих собственным функциям Ψn,l,m(r,ϑ,ϕ), дискретен (см. рис. 1 и 2):
En = − |
m e4 |
1 |
, |
|
|
e |
|
|
(3) |
||
32π 2h2ε02 |
|
(nr +l +1)2 |
|||
|
|
|
|
||
где nr – радиальное квантовое число, l – азимутальное квантовое число. Если ввести параметр n – главное квантовое число – так, что
n = nr + l +1, то
En = − |
m e4 |
1 |
, |
|
e |
|
|
||
|
|
|
|
|
|
32π2h2ε02 |
|
n2 |
|
где n = 1, 2, 3, … . Главное квантовое число n определяет значения энергии электрона в атоме водорода и совпадает с номером уровня энергии. При n = 1 Е1 = -13,55 эВ. Это самый нижний энергетический уровень, соответствующий основному, невозбужденному состоянию атома водорода. При отсутствии внешнего воздействия в стационарном
состоянии атом может находиться сколь |
угодно долго. |
По |
мере |
|||||||
E, U |
увеличения |
n |
|
энергетические |
||||||
уровни |
сгущаются |
|
(рис.1), |
при |
||||||
0 |
|
|
||||||||
|
|
|||||||||
|
r n → ∞ Е → 0, |
что |
|
соответствует |
||||||
E4 |
переходу |
электрона |
в |
состояние |
||||||
E3 |
покоя на бесконечности (ионизации |
|||||||||
E2 |
атома). |
|
|
|
|
|
(орбитальное) |
|||
|
U (r) |
Азимутальное |
l |
|||||||
|
квантовое |
|
число |
определяет |
||||||
|
|
модуль |
|
орбитального |
момента |
|||||
|
|
импульса электрона: |
|
|
|
|
||||
E |
|
|
|
Ll = h l(l +1). |
|
|||||
1 |
|
Если |
|
радиальное |
квантовое |
|||||
|
|
|
||||||||
|
Рис. 1 |
число |
nr |
= |
0, |
то |
при |
заданном |
||

3
значении главного квантового числа n азимутальное квантовое число l достигает максимального значения. Из n = nr + l +1 и n =lmax +1
следует, что lmax = n −1, то есть при заданном n азимутальное квантовое
число l может принимать n значений:
l = 0, 1, 2, …, (n – 1).
Кроме параметров n и l, собственные функции Ψn,l,m(r,ϑ,ϕ) зависят от параметра ml, который определяет ориентацию вектора орбитального
→ |
→ |
момента импульса L l в пространстве. Вектор |
L l момента импульса |
электрона может иметь лишь такие ориентации в пространстве, при которых его проекция на выделенное в пространстве направление z (направление магнитного поля) принимает значения
Llz =hml ,
где магнитное квантовое число ml при заданном l может принимать 2l+1 значений.
ml =0,±1,±2,...,±l,
→
что соответствует 2l+1 ориентациям вектора L l в пространстве. Установлено, что электрон имеет собственный механический
→
момент Ls , модуль которого равен
Ls = h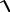 s(s +1),
s(s +1),
где s – спиновое квантовое число (s = ½), и собственный магнитный
|
→ |
|
|
|
момент |
p ms . Проекция собственного механического момента на |
|||
направление z внешнего магнитного поля равна |
||||
|
Lsz = hms , |
|||
где ms |
- магнитное спиновое квантовое число (ms = ± 12) . Проекция |
|||
|
→ |
|
|
|
собственного магнитного момента p ms |
на направление z равна |
|||
|
pmsz = ± |
|
eh |
. |
|
|
|
||
|
|
2me |
||
Введение спина потребовало записи релятивистского уравнения Дирака, так как из уравнения Шредингера наличие спина у электрона

4
не следовало. Для малых скоростей электрона в электромагнитных полях уравнение Дирака переходит в уравнение Паули. (Уравнение Паули – уравнение нерелятивистской квантовой механики, описывающее движение заряженных частиц со спином 12 во внешнем
электромагнитном поле – является обобщением уравнения Шредингера).
Таким образом, состояние электрона в атоме необходимо описывать набором четырех квантовых чисел:
главного n |
(n = 1, 2, 3, …), |
азимутального l |
(l = 0, 1, 2, …, n-1), |
магнитного ml |
(ml = -l, -(l-1), …, -1, 0, 1, …, l), |
магнитного спинового ms |
(ms = +1/2, -1/2). |
Так как энергия электрона Еn в атоме водорода зависит только от главного квантового числа n, то каждому собственному значению энергии (кроме основного состояния Е1) соответствует несколько собственных функций Ψn,l,m, отличающихся параметрами l и ml. Состояния, описываемые такими собственными функциями, называются вырожденными, а число состояний – кратностью вырождения по l и ml. Кратность вырождения уровня Еn равна
n−1
∑(2l +1)= n2 .
l=0
Вспектроскопии приняты следующие обозначения состояний:
|
Название состояний |
Обозначения |
0 |
s – состояние |
ns |
1 |
p – состояние |
np |
2 |
d – состояние |
nd |
3 |
f – состояние |
nf |
4 |
g – состояние |
ng |
… |
… |
… |
Например, 5f-состоянию соответствуют n = 5, l = 3.
В атоме водорода все состояния, кроме основного, возбужденные. Любое возбужденное состояние нестационарно, то есть без внешнего воздействия из него возможны переходы в другие состояния с меньшей энергией. Переходы из одного разрешенного состояния в другое, сопровождаемые испусканием или поглощением кванта света (фотона), называют радиационными. Из решения уравнения Шредингера в
5
соответствии с требованиями закона сохранения момента импульса, его проекции на выделенное в пространстве направление, четности следуют условия изменения квантовых чисел l и m при переходе атома из одного состояния в другое при радиационных переходах – правило отбора:
1)изменение азимутального квантового числа ∆l удовлетворяет условию ∆l = ±1;
2)изменение магнитного квантового числа ∆ml удовлетворяет
условию ∆m = 0,±1.
Закон сохранения энергии позволяет найти энергию испущенного (или поглощенного) фотона εф :
εф = Ei − Ek = hω = 2πhc / λ, |
(4) |
где Ei и Ek вычисляются по формуле (3); ω - частота испущенного кванта света; с – скорость света в вакууме; λ - длина волны света в вакууме.
В спектре атома водорода спектральные линии группируются в спектральные серии, названные именами известных спектроскопистов. Из соотношений (3) и (4) следует:
1 |
|
me e |
4 |
|
1 |
|
1 |
|
|
1 |
|
1 |
|
|
||||
= |
|
|
|
− |
|
|
− |
|
(5) |
|||||||||
|
|
3 |
|
3 |
2 |
2 |
2 |
2 |
2 |
|||||||||
λ |
64π |
h |
|
|
= R |
, |
||||||||||||
|
|
|
|
cε0 |
ni |
|
nk |
|
ni |
|
nk |
|
|
|||||
где
R = |
me e4 |
− |
(6) |
|
64π 3 h3 cε02 |
||||
|
|
|
постоянная Ридберга (иногда постоянную Ридберга рассматривают в виде
R′ = |
|
|
me e4 |
|
|
). |
(7) |
||||||
64π 3h3ε |
02 |
||||||||||||
|
|
|
|
|
|||||||||
Из формулы (5) при ni = 1, nk = 2, 3, 4, … получаем серию Лаймана |
|
||||||||||||
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|||||||
|
|
= |
|
|
2 − |
2 |
|
|
(8) |
||||
|
λ |
R |
1 |
|
; |
||||||||
|
|
|
|
|
nk |
|
|
|
|
||||
при ni = 2, nk = 3, 4, 5, … — серию Бальмера (см. рис. 2, табл. 1)
1 |
|
1 |
|
1 |
|
|
||
|
− |
|
(9) |
|||||
|
|
2 |
2 |
|||||
λ |
= R |
2 |
; |
|||||
|
|
|
nk |
|
|
|||

6
Энергия, эВ
|
n |
s |
p |
d |
f |
0 |
∞ |
l = 0 |
l = 1 |
l = 2 |
l = 3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
-1 |
5 |
|
|
|
|
4 |
|
|
|
|
|
|
3 |
|
|
|
|
-2 |
|
|
|
|
|
-3
2
-4 |
Серия Бальмера |
|
|
|
Рис. 2 |
при ni = 3, nk = 4, 5, 6, … — серию Пашена
1 |
|
1 |
|
1 |
|
|
||
|
− |
|
(10) |
|||||
|
|
2 |
2 |
|||||
λ |
= R |
3 |
; |
|||||
|
|
|
nk |
|
|
|||
и т.д. Серия Лаймана (8) расположена в ультрафиолетовой области спектра, серия Пашена (10) и все последующие серии – в инфракрасной области спектра.
В данной работе изучаются линии серии Бальмера (8). Первые четыре линии этой серии (табл. 1) расположены в видимой части спектра, остальные – в ультрафиолетовой.
|
|
|
Таблица 1 |
|
Линия |
Длина волны, |
Цвет |
Соответствующие переходы |
|
|
нм |
|
(см. рис. 2) |
|
Нα |
656, 2785 |
Красная |
3s → 2p, 3p → 2s, 3d → 2p |
|
Нβ |
486, 1319 |
Зелено-голубая |
4s → 2p, 4p → 2s, 4d → 2p |
|
Нγ |
434, 0459 |
Сине-фиолетов. |
5s → 2p, 5p → 2s, 5d → 2p |
|
Нδ |
410, 1731 |
Фиолетовая |
6s → 2p, 6p → 2s, 6d → 2p |
|
Нε |
397, 0068 |
Ультрафиолет. |
7s → 2p, 7p → 2s, 7d → 2p |
|
388, 9045 |
Ультрафиолет. |
|||
Нξ |
8s → 2p, 8p → 2s, 8d → 2p |
|||
… |
… |
|||
… |
… |
|||
|
|
Линия Нα — головная линия серии Бальмера – самая яркая (см. рис. 3), яркость последующих линий убывает так, что линия Нδ может наблюдаться не для всех источников и не в каждом спектральном приборе. Линии в серии сгущаются около коротковолновой границы
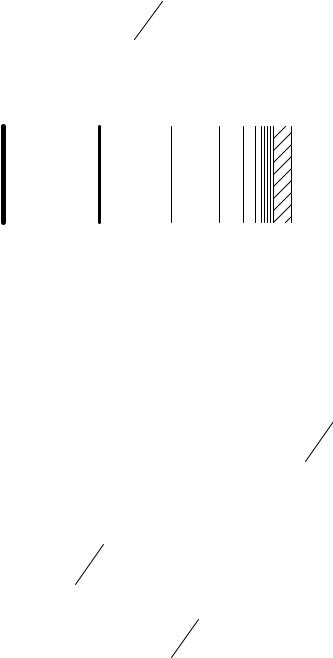
7
спектра (n → ∞). К ней примыкает непрерывный спектр (ультрафиолетовый свет). Длина волны, соответствующая границе серии:
λгр = 4 |
R |
. |
(11) |
|
|
|
Hα |
Hβ |
Hγ Hδ |
H∞ |
Рис. 3
Очевидно, переходы, при которых излучаются линии серии
Бальмера: |
(12) |
np → 2s, ns → 2p, nd → 2p, где n = 3, 4, 5, … . |
|
Зная постоянную Ридберга, можно найти энергию |
ионизации |
атома водорода (энергию, необходимую для отрыва электрона от атома) и потенциал ионизации:
εион = 2πhсR; |
ϕион = Еион |
e |
. |
(13) |
|
|
|
|
Ядро (протон) имеет конечную массу, а значит движение электрона с ядром происходит вокруг общего центра масс, поэтому в формулу постоянной Ридберга вместо массы электрона войдет
приведенная масса µ = me M (me + M ), |
|
где М – масса ядра. С учетом |
||
этого постоянная Ридберга принимает значение |
|
|||
|
m |
|
|
(14) |
Rтеор. = R∞ 1 − |
|
e |
, |
|
|
|
|
M |
|
где R∞ — постоянная Ридберга, вычисленная в предположении бесконечно тяжелого ядра (то есть по формуле (6)).
5. Практическая часть
Спектральный прибор, пространственно разделяющий лучи различных длин волн, основной своей частью может содержать дифракционную решетку или призму. Свет от источника попадает на
8
входную щель прибора, наблюдение спектра производят в зрительную трубу или лупу (см. инструкцию к прибору).
I. Градуировка спектрометра
Для градуировки спектрометра используют ртутную лампу. Спектральные линии ртутной лампы ДРШ приведены в табл. 2.
|
|
|
Таблица 2 |
№ |
Цвет |
Длина волны, |
Показания |
п/п |
|
нм |
барабана N |
1 |
Темно-красная |
690,716 |
|
2 |
Красная |
671,617 |
|
3 |
Красно-оранжевая |
623,437 |
|
4 |
Красно-оранжевая |
612,327 |
|
5 |
Красно-оранжевая |
607,264 |
|
6 |
Желтая |
579,066 |
|
7 |
Желтая |
576,960 |
|
8 |
Зеленая |
546,072 |
|
9 |
Голубая |
491,600 |
|
10 |
Синяя |
435,834 |
|
11 |
Сине-фиолетовая |
433,9 |
|
12 |
Фиолетовая |
407,9 |
|
13 |
Фиолетовая |
404,677 |
|
Примерный атлас спектральных линий изображен на рис.4. Включите источник питания ртутной лампы, небольшим
перемещением лампы относительно входной щели прибора добейтесь, чтобы в поле зрения окуляра спектральные линии имели максимально возможную яркость. Перемещением спектральной картины относительно визирной линии (перемещение в зависимости от конструкции прибора производится с помощью микровинта или с помощью окуляра) совмещайте каждую из спектральных линий, указанных в атласе (или в табл.2) с визирной линией. Соответствующие показания барабана (или шкалы) занесите в табл. 2. Постройте градуировочную (дисперсионную) кривую, на оси абсцисс откладывайте показания N барабана (шкалы) в делениях, на оси ординат – длину волны λ в выбранных единицах.

9
690 |
671 |
623 |
612 |
607 |
579 577 |
546 |
492 |
436 |
434 |
408 |
405 |
700 |
600 |
500 |
400 |
λ , нм |
|
|
Рис. 4 |
|
|
II.Определение постоянной Ридберга
1.Вместо ртутной лампы перед входной щелью спектрометра поставьте водородную лампу, включите ее блок питания, добейтесь наибольшей яркости спектральных линий в поле зрения окуляра,
измерьте положение линий Нα, Нβ, Нγ, Нδ. Результаты измерений занесите в табл. 3.
|
|
|
|
|
|
|
Таблица 3 |
|
|
|
|
|
|
|
|
|
|
|
Показания |
Длина |
|
Постоянная Ридберга |
||||
Линия |
барабана N |
волны λ |
Rэксп |
|
< Rэксп > |
Rтабл |
|
Rтеор |
|
дел. |
м |
м-1 |
|
м-1 |
м-1 |
|
м-1 |
Нα |
|
|
|
|
|
|
|
|
Нβ |
|
|
|
|
|
|
|
|
Нγ |
|
|
|
|
|
|
|
|
Нδ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. По градуировочному графику найдите соответствующие длины волн, сравните полученные результаты с длинами волн, приведенными в табл. 1. По формуле (9) вычислите экспериментальное значение постоянной Ридберга Rэксп = R∞. для каждой длины волны. Найдите среднее значение < Rэксп > = < R∞ >.
3.По формуле (6) вычислите табличное значение R∞табл, сравните с
<Rэксп >, сделайте выводы. По формуле (14) вычислите теоретическое
значение постоянной Ридберга, сравните с R∞табл и < Rэксп >.
