Емелянов Фундаменталные симметрии 2008

Мы не будем доказывать эту теорему (см. главу 2), а покажем, как она применяется. Сначала рассмотрим действие СРТ преобразования на электромагнитные взаимодействия. Используя соотношения

(6.14), (6.16), (6.21), (6.25), (6.54) и (6.58) получаем

инвариантно относительно С, Р и Т преобразований. СРТ- инвариантность, если это общее свойство, должна выполняться даже при нарушении отдельных симметрий. Наиболее значимую проверку предоставляет электрослабая теория. В этой теории С и Р нарушаются во взаимодействиях нейтральных токов, однако Т и СРТ сохраняются. Проверим это. Действие для взаимодействующих нейтральных токов

содержит как векторную, так и псевдовекторную части, поскольку последняя присутствует в SU(2)-токе J3μ . Четность и зарядовая

четность в соотношении (6.79) нарушены, поскольку векторный и псевдовекторный токи изменяются по-разному при действии этих преобразований. Действительно, при Р-преобразовании

С другой стороны, в соотношении (6.79) Т-инвариантность сохраняется, поскольку при обращении времени

Используя соотношения (6.81)–(6.83), можно показать, что взаимодействие нейтральных токов сохраняют СРТ. Действительно

Очевидно, что СР и Т-преобразования для действия, содержащего нейтральные токи, являются эквивалентными

Эквивалентность между Т и СР-преобразованиями имеет место даже в случае нарушения обеих симметрий. В этом случае комбинированное СРТ-преобразование сохраняет действие. В этом состоит существо СРТ-теоремы. В качестве пояснения, исследуем Т-нарушающее заряженное взаимодействие между u и b – кварками, определяемое комплексным матричным элементом матрицы СКМ Vub

Wubзаряж.ток CP→Wubзаряж.ток =

Из этого примера можно понять, почему справедлива СРТ-теорема. Она возникает из комбинации эрмитовости лагранжиана и той роли, которую Т и СР играют при их действии на С-числа, входящие в лагранжиан. Эрмитовость означает, что заданный член в лагранжиане, содержащий некоторый оператор O(6.x) и некторое С-число а, имеет вид

Под действием Т оператор не меняется (6.за исключением замены t→-t), с – число испытывает комплексное сопряжение

Относительно же преобразования СР, оператор О переходит в эрмитово сопряженный, С-число же не меняется

Объединение же операций Т и СР изменяет эффективно первое слагаемое в (6.96) на второе слагаемое и т.д.

6.6. С,Р,Т нарушаются, нарушается ли СРТ?

С, Р, Т симметрии с очень высокой степенью точности сохраняются в электромагнитных и сильных взаимодействиях. Стопроцентное нарушение Р и С открыто в слабых взаимодействиях в 1957 г. СР нарушение в распадах нейтральных каонов обнаружено

224

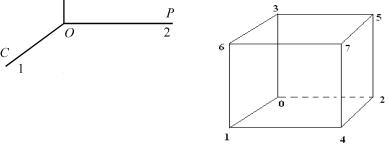
в 1964 г., а в распадах В-мезонов – в 1999 г., но мы до сих пор не знаем природы СР-нарушения. Найдено Т-нарушение в системе нейтральных мезонов и подтверждена СРТ-инвариантность. Что касается гравитации, то трудно предположить экспериментальную проверку С, Р, Т в классическом слабом гравитационном поле, эффекты же квантовой гравитации относятся к Большому Взрыву и образованию черных дыр. Обсудим эффекты нарушения семи симметрий: С, Р, Т, СР, РТ, СТ и СРТ в лабораторных экспериментах. Начнем обсуждение с трех ортогональных осей, представляющих нарушение С, Р и Т, (рис. 6.1)

Точка О на рис. 6.2 в начале координат соответствует взаимодействиям, которые С-четные, Р-четные, Т-четные, следовательно, СР-четные, РТ-четные, СТ-четные СРТ-четные.

Точка 1 соответствует взаимодействиям, которые С-нечетные, Р-четные, Т-четные, следовательно, СР-нечетные, РТ-четные, СТ- нечетные СРТ-нечетные.

Точка 2 соответствует взаимодействиям, которые С-четные, Р- нечетные, Т-четные, следовательно, СР-четные, РТ-нечетные, СТ- четные и СРТ-нечетные.

Точка 3 соответствует взаимодействиям, которые С-четные, Р- четные, Т-нечетные, следовательно, СР-четные, РТ-нечетные, СТ- нечетные и СРТ-нечетные.

Таким образом, строятся первые четыре вершины СРТ-куба. Теперь перейдем к другим вершинам (рис. 6.2): три в плоскостях СР

225

(точка 4), РТ (точка 5) , СТ (точка 6) и последняя вне этих плоскостей (точка 7).

Точка 4 соответствует взаимодействиям, которые С-нечетные, Р-нечетные, Т-четные, следовательно, СР-четные, РТ-нечетные, СТ-нечетные и СРТ-четные.

Точка 5 соответствует взаимодействиям, которые С-четные, Р- нечетные, Т-нечетные, следовательно, СР-нечетные, РТ-четные, СТ-нечетные и СРТ-четные.

Точка 6 соответствует взаимодействиям, которые С-нечетные, Р-четные, Т-нечетные, следовательно, СР-нечетные, РТ-нечетные, СТ-четные и СРТ-четные.

Точка 7 соответствует взаимодействиям, которые С-нечетные, Р-нечетные, Т-нечетные, следовательно, СР-четные, РТ-четные, СТ-четные и СРТ-нечетные.

Таким образом, для каждого из семи преобразований имеются четыре четные вершины и четыре нечетные.

Для С-преобразования вершины 0,2,5,3 – четные; 1,4,7,6 – нечетные.

Для Р-преобразования вершины 0,3,6,1 – четные; 2,5,7,4 – нечетные.

Для Т-преобразования вершины 0,1,4,2 – четные; 3,6,5,7 – нечетные.

Для СР-преобразования вершины 0,4,7,3 – четные; 1,2,5,6 – нечетные.

Для РТ-преобразования вершины 0,5,7,1 – четные; 2,3,6,4 – нечетные.

Для СТ-преобразования вершины 0,2,7,6 – четные; 1,3,5,4 – нечетные.

Для СРТ-преобразования вершины 0,4,5,6 – четные; 1,2,3,7 – нечетные.

6.6.1. С и Р-нарушение при сохранении СР

Начнем с (V-A)-взаимодействия слабых заряженных токов, открытых в 1957 г. Произведение VV и АА относится к точке О, а произведение к VA – к точке 4, поскольку векторный V ток С, Р, Т – нечетен, а аксиальный А ток С, Р –четен, но Т – нечетен. Экспери-

226

ментально произведение VA проявляется в распаде К1→2π, а VV – в распаде К2→3π, где К1 и К2 соответствуют С – нечетным и С – четным суперпозициям K 0 и K 0

Так как K1 и K2 оба Р-нечетные (псевдоскаляры), то K1– СР-четен, а K2 – СР-нечетен.

Двухпионное состояние с J = 0 С-четное, Р-четное и СР-четное. Следовательно, распад K10 → 2π С-нечетен, Р-нечетен и СР-

четен. Что касается трехпионного состояния с J = 0, то оно Р- нечетно независимо от величины относительного углового момента l и L. Доминантное состояние с l = L = 0 С-четно. Поэтому распад

K20 → 3π , главным образом, С-четен, Р-четен и СР-четен. VA-взаимодействие (точка 4) проявляется в корреляции между

спином и угловым моментом в β-распадах, распадах μ и τ- лептонов. Полулептонные распады мезонов и нелептонные распады гиперонов оказываются невозможными без интерференции членов VV и АА в квадратах модулей соответствующих амплитуд. То же самое относится к Р и С-нарушающим корреляциям, вызванным нейтральными токами, открытыми в 1970 г. Все эти процессы осуществляются виртуальными W и Z бозонами.

6.6.2. СР и Т-нарушения

Открытие в 1965 г. двухпионных распадов долгоживущих нейтральных каонов свидетельствовало о том, что СР-инвариантность нарушается. Эффективное взаимодействие, вызывающее эти распады соответствует точке (6) на рис. 6.2: оно С-нечетное, оно Р- четное и Т-нечетное, приводит к вакуумным переходам K2 в K1 и

описывается комплексным параметром ε:

Присутствие величины ε в соотношении (6.102) означает, что вероятность преобразования K в K в течение времени t не равно вероятности преобразования K в K за это же время. Действительно,

227

амплитуды различны из-за присутствия двух различных экспонент, описывающих распространение KL и KS . Это предсказание нару-

шения Т-инвариантности было экспериментально установлено в 1998 г. коллаборацией CPLEAR. Другое подтверждение нарушения Т-инвариантности получено в экспериментах по асимметрии между

плоскостями e+e− и π+π− , наблюдаемой в распадах

KL →π+π− e+e− .

Сравнительно недавно получено согласие в определении параметра ε′, описывающего прямой распад K2 на 2π. Этому процессу

отвечает точка 5 на рис. 6.2 (С-четные, Р-нечетные и Т-четные). Точка 5 также определяет электрические дипольные моменты таких частиц, как нейтрон и электрон. Действительно, дипольный

момент определяется членом в гамильтониане σ E , где σ пред-

ставляет собой спин частицы, E – электрическое поле. Этот член С-четный, Р-нечетный и Т-четный, т.е. взаимодействие СРТ- инвариантно.

Подчеркнем, что на уровне стандартного электрослабого лагранжиана точки 5 и 6 имеют общее происхождение: фазу СКМ матрицы заряженных кварковых токов. Особый интерес к точке 5 связан с очень малым значением θ-члена КХД

где Gμν – тензор напряженности глюонного поля.

6.6.3. СР-нарушающие зарядовые асимметрии

Точки 5 и 6 должны проявлять себя в зарядовых асимметриях. Из соотношения (6.102) следует, что ширины полулептонных рас-

падов KL → e+νeπ− и KL → e−νeπ+ должны быть разными, причем величина эффекта пропорциональна 2Reε. Эта зарядовая асимметрия измеряется как в электронном, так и в мюонном каналах. Еще одна зарядовая асимметрия была предсказана Okubo еще до открытия СР-нарушения, но она пока не измерена. Согласно Okubo

Чтобы показать, как появляются эти эффекты, заметим, что амплитуды S и P волн

где A3 и A1 – амплитуды конечных состояний с изоспином Т = 3/2 и Т = 1/2. Подобные же соотношения имеют место для античастиц

Для простоты рассмотрим только S-волновые амплитуды. При этом мы не теряем общности, поскольку S- и Р-волны в выражениях для парциальных ширин не интерферируют. Модули изотопических амплитуд, как и фазовые сдвиги, вследствие взаимодействий в конечном состоянии, одинаковые для частиц и античастиц

(A1 = A1, A3 = A3, δ1 = δ1, δ3 = δ3 ) , однако СР-нарушающие фазы

6.6.4. Проверки СРТ с античастицами

Вера в СРТ-инвариантность основана на квантовой теории поля, в частности, на локальности лагранжиана, его лоренцинвариантности и эрмитовости. Можно ожидать, что квантовая теория поля является некоторым приближением более фундаментальной теории (суперструн?). Так или иначе, независимо от конкретного источника СРТ-нарушения, для сравнения предсказаний теории с экспериментом используется терминология квантовой теории поля.

Большинство явлений, предлагаемых для проверки СРТ- симметрии, относятся к точке 1: они С-нечетны и РТ-четны. К ним относятся:

229

1) поиски разницы в массах частиц и античастиц ( mK 0 − mK 0 ,

mK + − mK − , me− − me+ , mn − mn и т.д.);

2) поиски отличных от нуля сумм магнитных моментов частиц и античастиц ( μμ+ ≠ −μμ− , μe+ ≠ −μe− , μp+ ≠ −μp− и т.д.).

Особенно популярны рассуждения об отличных от нуля разностях масс нейтрино и антинейтрино. Большинство этих рассуждений связано с нарушением Лоренц – инвариантности и (или) локальности. СРТ – нарушающий эффект, вследствие интерференции точек 3 и 0, мог бы проявляться в поляризации мюона, перпенди-

кулярной плоскостям распада KL0 → μ+νμπ− и KL0 → μ−νμπ+ , если бы она была одинаковой для обоих распадов. В этом случае корре-

тельно, эта корреляция СРТ нечетна. Однако «фальшивое» Т-на- рушение, могло быть вызвано пион-мюонным рассеянием в конечном состоянии в точке 0 с фазой δ ~ α/3. Экспериментальный верхний предел на эту поляризацию составляет 0.5%. Заметим, что та-

кая же поперечная поляризация в распадах K + → μ+νμπ0 и

K − → μ−νμπ0 не может быть фальшивой из-за электромагнитного

рассеяния в конечном состоянии.

В качестве примера проявления точки 7 рассмотри электрический дипольный момент частицы и античастицы, скажем, e− , e+ и νe , νe . Если Р и Т – нарушены, а С – сохраняется (точка 6), элек-

трические дипольные моменты отличны от нуля, однако их сумма должна обращаться в ноль, поскольку они (подобно зарядам и магнитным дипольным моментам, описываемым точкой 0) должны иметь противоположные знаки. Это следует из отрицательной С- четности фотона.

Если снова обратиться к точке 7, то обнаружим, что она должна быть не только Р и Т-нечетной, но и С-нечетной. Это обстоятельство требует дополнительного слагаемого в лагранжиане, которое приводит не только к тому же абсолютному значению, но и к одному знаку электрических дипольных моментов частицы и анти-

230