
Добродеев Колебания и оптика. Атом и атомное ядро 2011
.pdf
3) тогда ω0= |
k |
. |
|
||
|
m |
|
Пример 2.1. К нижнему концу пружины прикреплен небольшой шарик массы m, верхний конец пружины закреплен. Жесткость пружины k. Определить период свободных колебаний шарика.
Решение. На рис. 2.1 изображен в двух положениях вертикальный пружинный маятник – так иногда называют эту систему: справа – в положении равновесия, слева – и произвольном положении, когда координата конца пружины равна х.
Запишем для этого положения вто-
рой закон Ньютона для шарика:
Рис. 2.1
m a = m g + F ,
где F − сила упругости пружины, которая пропорциональна полному растяжению:
Fx = − k (x + lP − l0 );
lP − длина пружины в равновесии, l0 – длина недеформированной пружины.
Второй закон Ньютона в проекции на ось 0Х запишется в виде:
max = − kx − k (lP − l0) + mg.
Учтем, что в равновесии
k (lP − l0) = mg.
Таким образом, окончательно
max = − kx, ω0 = |
k |
. |
|
||
|
m |
|
Ответ: Т = 2π m / k .
Можно сделать вывод, что собственная частота колебаний вертикального и горизонтального пружинных маятников одинакова.
Пример 2.2. Однородный цилиндр с площадью основания S плавает на границе двух несмешивающихся жидкостей, плотности которых ρ1 и ρ2. Найти период Т малых колебаний цилиндра.
11

Решение. На рис. 2.2 изображен в двух положениях цилиндр, плавающий на границе двух жидкостей: слева – в положении равновесия, справа – в произвольном положении, когда координата дна цилинд-
ра равна х.
Запишем для произвольного положения второй закон Ньютона для шарика:
|
|
|
|
ma = mg + F1 + F2 |
|
|
Здесь |
F |
, |
F |
|
|
1 |
2 − силы Архимеда, дей- |
|||
|
ствующие со стороны первой и второй |
||||
Рис. 2.2 |
|||||
жидкости. |
|
|
|
||
|
|
|
|
||
Второй закон Ньютона в проекции на ось 0Х запишется в виде:
max = − ρ1S(l1 − x)g − ρ2S(l2 +x)g + mg
(S – площадь основания цилиндра, l1 и l2− соответствующие высоты частей цилиндра, погруженных в первую и вторую жидкости в равновесии).
Учтем, что в равновесии ρ1Sl1g+ ρ2Sl2g = mg. Тогда окончательный вид второго закона Ньютона
max = − (ρ2 − ρ1)Sg x,
а собственная частота
|
ω0= |
(ρ2 |
− ρ1 )Sg |
. |
|
|
|
|
m |
||
|
|
|
|
|
|
Ответ: Т = 2π |
m |
|
. |
|
|
(ρ2 − ρ1 )Sg |
|
|
|||
Пример 2.3. Период колебаний математического маятника на высоте Н над поверхностью Земли равен Т. В шахту какой глубины h надо опустить этот маятник, чтобы этот период не изменился?
Решение. Период колебаний математического маятника Т = =2π l / g , где l – длина нити, g – ускорение свободного падения в
том месте, где находится маятник.
Связь между ускорением свободного падения g0 на поверхности Земли и ускорением gН на высоте Н над поверхностью Земли получается из второго закона Ньютона:
12

mg0 = G mM , mgH = |
|
mM |
, |
|
|
||
(R + H )2 |
|||||||
R2 |
|
|
|
||||
где M и R – масса и радиус Земли, G – гравитационная постоянная. |
|||||||
Из этих соотношений gH = g0 |
R2 |
|
. |
|
|
|
|
|
|
|
|
||||
(R + H )2 |
|
|
|
||||
|
|
|
|
||||
Связь между ускорением g0 и ускорением
gh на глубине h получается тоже из второго закона Ньютона, но сила притяжения Земли в шахте определяется по-другому.
На тело массы m, находящееся в шахте на глубине h, действует только масса Mh шара радиуса R – h. Земные слои, расположенные
выше, дают равнодействующую, равную нулю (аналогично тому, что на точечный заряд, помещенный внутри заряженной сферы, не действует сила).
Сила притяжения поэтому
|
|
|
|
|
|
|
|
|
F = G |
|
mM h |
, |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
(R − h)2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а так как Mh = |
|
M |
|
|
4π(R − h)3 / 3 |
= M |
|
(R − h)3 |
, то |
|
|
||||||||||||||||||||
|
4πR3 / 3 |
|
|
|
R3 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
mM |
|
R − h |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
F = G |
|
. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
R |
|
|
|
|
|
|
|
|
|
|
|
||||
Запишем еще раз второй закон Ньютона: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
mg0 |
= G mM |
, mgh |
= G mM |
|
R − h |
, |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
откуда |
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
R2 |
|
|
R |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R − h |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
gh = g0 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
R2 |
|
||
Период не изменится, если gh = gH |
или |
|
R − h |
= |
, и |
||||||||||||||||||||||||||
|
|
R |
(R + H )2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
R |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
окончательно |
h = |
R 1 |
− |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(R |
+ H ) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
R |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: h = R 1 − |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(R + H ) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
13

Пример 2.4. На сколько отстанут за сутки маятниковые часы, поднятые на вершину Эвереста (h = 8,9 км)? Радиус Земли R = = 6400 км.
Решение. Согласно выводам предыдущей задачи период коле-
баний маятника на высоте H ТH = 2π |
|
l |
будет больше периода |
|||
|
|
|
|
gH |
||
колебаний на поверхности Т0 = 2π |
l |
|
, и одно колебание на высо- |
|||
g0 |
||||||
|
|
|
|
|||
те длится на ∆Т = ТH − Т0 дольше. Отставание за время t = 1 сут = = 24·3600 c будет равно
τ = N∆Т = |
t |
∆Т = |
t |
(ТH − Т0) = t ( |
TH |
− 1) = t ( |
g0 |
− 1). |
||
T |
T |
T |
||||||||
|
|
|
|
g |
H |
|
||||
|
0 |
|
0 |
0 |
|
|
|
|||
Здесь N − число колебаний маятника за сутки.
R2
Так как gH = g0 (R + H )2 , то окончательно
τ = |
t H |
= |
24 3600 8,9 103 |
= 120 с. |
|
R |
6, 4 106 |
||||
|
|
|
Ответ: τ = tHR = 120 с.
Задачи для решения в классе и дома
2.1.Груз колеблется по вертикали на резиновом шнуре. Во сколько раз изменится период вертикальных колебаний груза, если его подвесить на том же шнуре, сложенном вдвое?
2.2.Во сколько раз изменится частота колебаний автомобиля на рессорах после принятия груза, равного массе порожнего автомобиля?
2.3.К свободному концу вертикальной легкой пружины, прикрепленной к потолку, подвешивают груз (пружина не деформирована) и отпускают его без начальной скорости. Амплитуда возникших колебаний А. Найдите период Т колебаний груза и его максимальную скорость υm.
2.4.Подвешенный на легкой нити маленький шарик движется в горизонтальной плоскости по окружности радиусa R << l (l – длина нити). Покажите, что период движения шарика по окружности равен периоду малых колебаний математического маятника.
14
2.5.Тело совершает колебания по закону x(t) = Acos(ωt + φ0). Масса тела m. Найдите зависимость от времени Fx(t) и от смещения Fx(х) проекции равнодействующей всех сил, приложенных к телу. Чему равен коэф-
фициент пропорциональности k между силой Fx и смещением х при гармонических колебаниях тела (коэффициент квазиупругой силы)?
2.6.Пробирка с дробью на дне плавает в воде. Площадь поперечного сечения пробирки S, ее масса (с дробью) m. Найдите круговую частоту и период вертикальных колебания пробирки.
2.7.Нерастянутый легкий резиновый шнур длиной l0 = 25 см закреплен концами в горизонтальном положении. С подвешенным посередине грузом шнур в положении равновесия удлиняется вдвое. Найдите частоту ω0 малых вертикальных колебаний груза.
2.8.Определите время τ полета камня от одного полюса Земли до другого по прямому тоннелю, если его прорыть через центр Земли. Плотность Земли считать постоянной, радиус Земли R = 6400 км.
2.9.Небольшое тело находится на дне чаши, внутренняя поверхность которой представляет собой сферический сегмент радиусa R. Определить период малых колебаний Т тела при выведении его из положения равновесия.
2.10.Шарик на нити (математический маятник) совершает малые ко-
лебания. Найдите коэффициент пропорциональности k между силой Fx, возвращающей шарик в положение равновесия, и его смещением х из положения равновесия (коэффициент квазиупругой силы). Получите формулу для расчета периода колебаний.
2.11.Какое значение получил для ускорения свободного падения учащийся при выполнении лабораторной работы, в которой маятник длиной l = 90 см совершил за τ = 1 мин n = 30 колебаний?
2.12.За одно и то же время один математический маятник делает
n1 = 50 колебаний, а второй n2 = 30 колебаний. Найдите их длины, если один из них на ∆l = 32 см короче другого.
2.13.Вблизи рудного месторождения период колебаний маятника изменился на β = 0,001. Плотность руды в месторождении ρ = 8 г/см3. Оце-
ните радиус месторождения r, считая его шаровым, если средняя плотность Земли ρ0 = 5,6 г/см3, радиус ЗемлиR = 6400 км.
2.14.Математический маятник длиной l совершает малые колебания.
Найдите зависимости от времени тангенциального аτ(t) и нормального аn(t) ускорений шарика. Чему равны и при каких положениях шарика достигаются максимальные значения этих величин, если l = 10 см, амплитуда
А= 5 мм?
15
2.15. Определите период малых колебаний математического маятника, подвешенного к потолку лифта, если лифт движется с ускорением а = 3,2 м/с2, направленным: 1) вверх; 2) вниз. Тот же маятник колеблется с периодом Т0 = 2,2 с в равномерно движущемся лифте.
2.16. В ракете, движущейся с ускорением a = − g0 ( g0 − ускорение
свободного падения вблизи поверхности Земли), колеблется математический маятник длиной l = 1 м. Каков период колебания этого маятника, если высота ракеты над поверхностью Земли равна радиусу Земли?
2.17.Найдите период колебаний математического маятника длиной l, подвешенного в вагоне, движущемся горизонтально с ускорением а.
2.18.Шарик массой m, подвешенный на нити, совершает малые колебания. Во сколько раз η возрастет частота колебаний, если шарику сообщить положительный заряд q и поместить его в однородное электрическое поле напряженностью Е, направленной вертикально вниз?
2.19.Две пружины жесткостью k1 и k2 соединили последовательно и подвесили на них тело массой m. Каков период Т вертикальных колебаний системы?
3. Энергия гармонических колебаний. Вынужденные колебания
В процессе колебаний происходит превращение кинетической энергии K в потенциальную П и обратно.
Полная энергия маятника в произвольный момент
E = K + П = mυ2/2 + kx2/2
сохраняется при свободных колебаниях, если силы сопротивления пренебрежимо малы. Это справедливо для колебаний как под действием упругих сил, так и под действием квазиупругих сил. В этом соотношении m – некоторая эффективная масса, k – коэффициент упругой или квазиупругой силы.
Учитывая, что в момент наибольшего отклонения (хmах = А) скорость υ = 0, а при х = 0 скорость максимальна и равна υmах, полную
энергию можно записать в виде: E = kА2/2 = mυmax2 /2 = m ω02 А2/2. В последнем учитывается равенство Vmах = ω0А.
Если силами сопротивления пренебречь нельзя, свободные колебания являются затухающими. Характер изменения координаты
16

колеблющей точки при небольшом сопротивлении приведен на рис. 3.1.
Рис. 3.1 |
Рис. 3.2 |
Характер изменения координаты колеблющей точки при вынужденных колебаниях приведен на рис. 3.2. Сначала идет процесс установления колебаний. Амплитуда возрастает до того момента, пока работа вынуждающей силы не совпадет с работой силы трения, и тогда возникает режим незатухающих или установившихся колебаний с частотой вынуждающей силы ω и определенной амплитудой.
При изменении частоты ω амплитуда изменяется и резко возрастает при приближении частоты ω к собственной частоте колебаний системы ω0. Это явление называется резонансом. На рис. 3.3 приведена зависимость амплитуды А от частоты ω при разных значениях коэффициентах сопротивления β. При больших β резонанс выражен слабо.
Примеры решения задач
Другим методом (один описан на с. 10) для нахождения собственной частоты ω0 колебаний системы является метод, основанной на применении выражения для энергии колебаний. Последовательность действий в этом методе такова:
1) написать выражение для полной энергии системы в произвольном положении;
17

|
привести его к виду E = |
mυ2 |
kx |
2 |
|
||||
2) |
x |
+ |
|
|
; |
||||
2 |
|
||||||||
2 |
|||||||||
|
|
|
|
|
|
|
|||
3) |
тогда ω0= |
k |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
m |
|
|
|
|
|
||
Замечание: так как скорость υх является производной от координаты х (υх = x′), то выражение для E имеет вид:
E = |
m ( x′)2 |
+ |
kx 2 |
, |
|
2 |
2 |
||||
|
|
|
причем в качестве координаты может быть не только х. В частности, для вращения это может быть угол поворота φ и, соответственно, угловая скорость ω = φ′.
Пример 3.1. К нижнему концу легкой нерастяжимой нити прикреплен небольшой шарик массы m, верхний конец нити закреплен. Длина нити l. Определить период T свободных колебаний шарика (эту систему часто называют математическим маятником).
Решение. На рис. 3.4 изображен математический маятник в произвольном положении – нить отклонена от вертикального положе-
ния на угол φ. |
|
||||
|
|
Полная энергия шарика E = |
mυ2 |
|
+ mgh. |
|
|||||
|
|
2 |
|
|
|
|
|
Выражаем h через угол φ: |
|
||
|
|
h = l(1 – cos φ) = 2l sin2(φ/2). |
|
||
φЕсли рассматривать малые углы, то
|
|
|
l |
sin(φ/2) ≈ φ/2 и h = lφ2/2. |
|||||
|
|
|
Учтем также, что υ = ωl = lφ′. |
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
Тогда выражение для полной энергии E |
||||
h |
|
|
|
m |
приобретает требуемый вид: |
|
|
||
|
|
|
|
|
|||||
|
|
|
|
|
E = ml 2 (φ′)2 |
+ mgφ2 . |
|||
|
|
Рис. 3.4 |
2 |
2 |
|
|
|||
|
|
Таким образом, ω0= |
mgl |
|
g |
. |
|||
|
|
|
|
|
= |
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
ml2 |
l |
||
Ответ: Т = 2π |
l / g . |
|
|
|
|
||||
Вывод: малые колебания математического маятника являются гармоническими с периодом Т = 2π l / g .
18
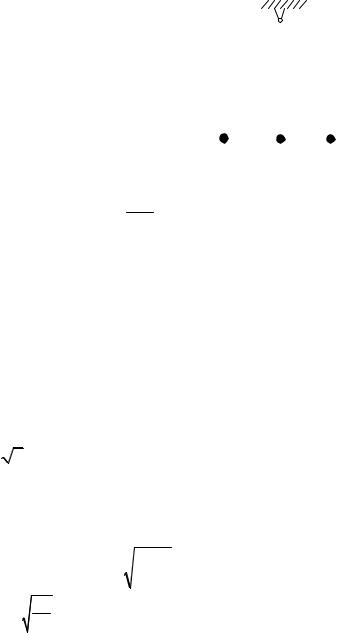
Пример 3.2. Жесткая конструкция состоит |
|
|
|
|
|
из трех легких стержней с закрепленными на |
|
О |
|
|
|
|
|
||||
них тяжелыми одинаковыми шариками и мо- |
|
|
|
|
|
жет свободно вращаться вокруг горизонталь- |
|
2l |
|
|
|
ной оси, проходящей через точку О, перпенди- |
|
|
|
|
|
кулярной плоскости конструкции. Длины |
|
|
|
|
|
стержней указаны на рис. 3.5. Определить пе- |
|
|
|
|
|
риод малых свободных колебаний в верти- |
l |
|
|
l |
|
кальной плоскости. |
Рис. 3.5 |
|
|||
Решение. Полная энергия системы равна |
|
||||
сумме кинетической и потенциальной энергий
E = K + П = mυ2 + mgh.
2
При отклонении центрального стержня на малый угол φ от положения равновесия потенциальная энергия левого шарика уменьшается, а правого увеличивается на ту же величину, то есть в сумме – нуль. Для центрального шарика потенциальная энергия такая
же, как и для математического маятника:
П = mg 2lφ2/2.
Рассчитаем кинетическую энергию системы. Она равна сумме кинетических энергий левого Kл, правого Kп и центрального Kц шариков:
K = Kл + Kп + Kц.
В силу симметрии
Kл = Kп = 5m(ωl)2/2,
так как V = ωl 5 ; Kц = 4m(ωl)2/2, поэтому
K = 9m(ωl)2/2.
|
9ml |
2 |
′ 2 |
|
|
2mglφ |
2 |
|
||
Полная энергия E = |
|
(φ ) |
+ |
|
, период |
|||||
|
|
2 |
2 |
|
|
|
||||
|
Т = 2π |
|
9ml 2 |
|
. |
|
|
|||
|
|
2mgl |
|
|
||||||
|
|
|
|
|
|
|
|
|||
Ответ: Т = 2π 29gl .
19

Пример 3.3. Построить график зависимости кинетической энергии от смещения при гармонических колебаниях пружинного маятника.
Решение. Поскольку полная энергия
|
сохраняется, то K = E − |
kx2 |
и график |
|
2 |
||
|
|
|
|
Рис. 3.6 |
будет иметь вид параболы, показанный |
||
на рис. 3.6. |
|
|
|
Пример 3.4. Найдите частоту ω и амплитуду А свободных колебаний частицы, если на расстояниях х1 и х2 от положения равновесия ее скорость равна соответственно υ1 и υ2.
Решение. Запишем закон сохранения энергии:
mυ2 |
kx |
2 |
|
mυ2 |
kx |
2 |
= |
kA2 |
|||
1 |
+ |
1 |
= |
2 |
+ |
|
2 |
|
. |
||
2 |
|
2 |
|
|
2 |
|
2 |
|
|
2 |
|
Здесь k – коэффициент квазиупругой (упругой) силы. Учитывая, что ω2 = k/m, разделив все равенства на m, получим:
υ2 |
+ω2 x2 =υ2 +ω2 x2 |
, |
|
υ2 |
+ω2 x2 |
= ω2 A2 . |
||||
1 |
|
1 |
2 |
2 |
|
|
1 |
|
1 |
|
Решение уравнений дает ответы. |
|
|
|
|
||||||
Ответ: ω = |
υ2 |
− υ2 |
, А = |
υ |
2 x2 |
− υ2 x2 |
|
|||
2 |
1 |
|
2 1 |
|
1 |
2 . |
|
|||
|
x2 |
− x2 |
|
|
|
x2 |
− x2 |
|
|
|
|
1 |
2 |
|
|
|
1 |
|
2 |
|
|
Задачи для решения в классе и дома
3.1.Получите зависимости от времени для потенциальной П(t) и кинетической K(t) энергий пружинного маятника. Постройте один под другим графики функций x(t), П(t), K(t). Как связана полная энергия маятника
Ес жесткостью пружины k и амплитудой колебаний А?
3.2.Математический маятник длиной l совершает малые колебания с амплитудой А. Масса шарика на нити m. Определите максимальную потенциальную энергию маятника. Как связана полная энергия маятника Е с коэффициентом квазиупругой силы k (см. задачу 2.10) и амплитудой колебания А?
3.3.Известны масса m, частота ν и амплитуда А гармонических колебаний материальной точки. Определите энергию колебаний Е.
3.4.При смещении тела из положения устойчивого равновесия на величину х возникает сила Fx = − 0,5х, возвращающая тело в прежнее поло-
20
