Диденко Сверхпроводясчие ускоряюсчие 2008

Реальная картина не столь оптимистична, так как примерно 1,5 Вт/м рассеивается в самой холодной части криостата, находящейся при температуре жидкого гелия. Необходимо принять во внимание также мощность от сети, потребляемую криогенной системой (рефрижератором), которая зависит от двух условий. Вопервых, это эффективность цикла Карно, составляющая η c=T/(300–

–T)=0,014 при Т=4,2К. Во-вторых, техническая эффективность, которая обычно не превышает 0,3. Таким образом суммарная эффективность рефрижератора при Т=4,2К составляет 0,0028. В случае медных резонаторов необходимо учитывать КПД СВЧ генератора, например, клистрона (около 0,5). Следовательно, при применении сверхпроводящих резонаторов потребление мощности сети меньше в 200 раз, чем при использовании медных резонаторов.

Преимущество сверхпроводящих резонаторов становится очевидным при применениях, требующих высокого ускоряющего напряжения в непрерывном режиме. Это особенно важно для накопительных колец. Поскольку рассеянная в стенках ускоряющей структуры мощность возрастает как квадрат напряженности поля, то только сверхпроводящие резонаторы могут обеспечить необходимое напряжение. Например, для ускорителя LEP требуется 2,5 ГВт, чтобы увеличить энергию с 50 до 100 ГэВ на пучок. Если использовать медные резонаторы при высоком ускоряющем градиенте, то установочная стоимость клистронов и потребляемая ими мощность питания становятся чрезмерными. Примерно 3 МВт/м мощности от сети потребуется для работы медных резонаторов при 5 МВ/м. При частоте 500 МГц это примерно 1 МВт на ячейку. Существуют практически установленные пределы по рас-

61

сеиванию мощности. Так, полагают, что величина этой мощности не должна превышать в медной ячейке 100 кВт, чтобы температура поверхности не превышала 100° С, иначе наблюдается ухудшение вакуума, проявляется напряжение в металле и вызванная ими усталость материала. Поэтому типичные значения поля в непрерывном режиме в медных резонаторах не превосходят 1 МВ/м. Более высокие поля (свыше 50 МВ/м) могут быть получены в медных резонаторах, но только с микросекундными длительностями импульсов.

При использовании высокочастотной сверхпроводимости в ускорительной технике важными являются понятия поверхностного сопротивления и ограничения электрического и магнитного полей.

Поверхностное сопротивление сверхпроводящих резонаторов рассчитывают в соответствии с теорией BCS по формуле (1.33). Перепишем ее в виде

где А – постоянная, зависящая от таких параметров сверхпроводника, как глубина проникновения, когерентная длина, скорость Ферми; средний путь между столкновениями; kB – константа

Больцмана; T – температура охлаждения; ω – угловая частота. Необходимая для разрушения пар энергия обозначена как 2∆ (T). Ширина запрещенной энергетической зоны связана с критической температурой (Ткр) сверхпроводника в соответствии с теорией

В то же время экспериментальное поверхностное сопротивление хорошо соответствует формуле

Здесь R0 является постоянной, и этот параметр называется оста-

точным поверхностным сопротивлением.

Рабочая температура сверхпроводящих резонаторов обычно выбирается так, чтобы первый член уравнения был уменьшен до экономически допустимых пределов. Остаточное сопротивление R0 зависит от ряда факторов. Рекордное значение составляет 1 нОм. Типичные значения R0 лежат в области 10...100 нОм.

62

Хорошо известно, что максимальные электрическое Емакс и магнитное Нмакс поля на поверхности сверхпроводящего резонатора определяют выбор достижимого ускоряющего градиента. Как Емакс, так и Нмакс повышаются пропорционально с ростом уско-

ряющего поля Еуск. Отношения Емакс/ Еуск и Нмакс/ Еуск являются постоянными и всецело определяются геометрией резонатора. Тра-

диционно полагали, что при оптимизации формы резонатора среди других факторов необходимо минимизировать Емакс/ Еуск из-за полевой эмиссии, которая увеличивалась экспоненциально с ростом Емакс. Примером является форма резонатора TESLA/TTF, предло-

женная в 1992 г.[2.1, 2.2].

Хотя контроль полевой эмиссии является практической проблемой, нет ясности в оценке основного теоретического предела для электрического поля в диапазоне 100− 200 МВ/м на поверхности ниобиевого сверхпроводника. Во многих резонаторах значения Емакс порядка 70 – 80 МВ/м были достигнуты с небольшой полевой эмиссией. Такого результата удалось достичь благодаря снижению уровня загрязнения поверхности частицами при использовании технологии промывания водой под высоким давлением и сглаженной поверхности резонатора после электрополировки.

Важным явлением, которое лимитирует достижимые высокочастотные магнитные поля, является «тепловое разрушение» (thermal breakdown) сверхпроводимости. Начинается оно в субмиллиметровых областях поверхности, имеющих из-за наличия дефектов высокие ВЧ потери. Когда температура внутри дефектов превышает критическую температуру перехода сверхпроводимости Тс, потери возрастают и большие области становятся нормальнопроводящими.

Типичное достигнутое значение поверхностного магнитного поля в одноячеечных резонаторах составляет 180− 190 мТл, но недавно в Корнельском университете было получено 209 мТл [2.3, 2.4]. В девятиячеечных резонаторах достигнуто170 мТл [2.4].

На первом этапе применения высокочастотных сверхпроводящих резонаторов основным ограничивающим фактором было явление вторичного резонансного электронного разряда – мультипакторного разряда (multipacting). Этот процесс, в котором большое число электронов возникает в малой области на поверхности резонатора, имеет резонансный характер. Когда возникают резо-

63

нансные условия, лавина поглощает СВЧ мощность, делая невозможным повышение поля путем увеличения подводимой ВЧ мощности. Электроны ударяются о стенки резонатора, приводя к значительному повышению температуры и в конечном итоге к тепловому разрушению сверхпроводимости.

С разработкой резонатора с эллиптическим профилем продольного сечения мультипакторный разряд больше не является проблемой в ускоряющих структурах со скоростью, равной скорости света. В резонаторе с закругленной формой электроны дрейфуют к области нулевого поля на экваторе. Здесь электрическое поле так мало, что вторичные электроны не могут получить достаточно энергии, чтобы возродиться (только двухточечный мультипактор возможен). Однако мультипакторный разряд еще является помехой для структур с низкой скоростью частиц, а также для устройств ввода мощности.

В противоположность пределу по магнитному полю, теоретический предел по допустимому электрическому полю на поверхности не обнаружен. Предполагается, что в ниобиевых сверхпроводящих резонаторах могут существовать поля до 220 МВ/м. Однако при высоких электрических полях появляется ограничение в сверхпроводящих резонаторах из-за полевой эмиссии электронов с участков резонатора с высоким электрическим полем. СВЧ мощность поглощается электронами и превращается в тепло при ударе электронов о стенки. Если эмиссия растет интенсивно при высоких электрических полях, то возможно тепловое разрушение сверхпроводимости. Тепловое разрушение сверхпроводимости происходит на дефектах размером от 0,1 до 1 мм.

Итак, при создании высокочастотных сверхпроводящих резонаторов приходится бороться с проявлением мультипакторного разряда, тепловым разрушением и полевой эмиссией. C 1974 года этим проблемам стали уделять особое внимание, поэтому сейчас многие вопросы решены, и достигнутый в настоящее время ускоряющий градиент в одиночном резонаторе на частоте 1300 МГц достигает 56 МВ/м, а в девятиячеечной структуре типа TESLA до

40 МВ/м.

Отметим возможности использования технологии тонких пленок для сверхпроводящих высокочастотных резонаторов. Основное их преимущество состоит в относительно невысокой стоимо-

64

сти. Новые сверхпроводящие материалы имеют более высокое критические значения Ткр и Нкр. Однако сильный спад собственной добротности ограничивает получение высокого градиента и обычно Еуск < 25 МВ/м. В CERN на резонаторе из Nb/Cu, полученном методом магнетронного распыления, реализован ускоряющий градиент 23 МВ/м на частоте 1,5 ГГц. В Университете г.Вупперталя в резонаторе из Nb3Sn/Nb c использованием техники вакуумного напыления металла получен ускоряющий градиент 15 МВ/м на частоте 1,5 ГГц [2.1].

2.2. Электродинамические характеристики сверхпроводящих резонаторов

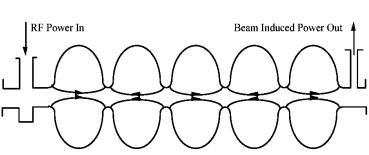
Сверхпроводящие резонаторы со скоростью частиц, равной скорости света, представляют собой структуры, развитые из резонаторов цилиндрической формы, возбуждаемых на колебании Е010. К резонатору добавляется трубка для пролета пучка, а цилиндрической поверхности придают эллиптическую форму для предотвращения мультипакторного разряда. На рис.2.1 представлен резонатор, состоящий из пяти ячеек. Резонансная частота обычно выбирается в диапазоне 300–3000 МГц. Длина каждой ячейки резонатора равна половине длины волны (λ /2). Очевидно, сдвиг фазы продольной составляющей электрического поля при переходе из одной ячейки к другой равен π . Заряженные частицы пересекают каждый полуволновый ускоряющий промежуток за половину ВЧ периода. В результате они находятся в ускоряющей волне на всей длине резонатора. В областях вне ячеек подсоединены узлы вводов мощности и устройства для вывода волн высших типов (ВВТ).

Рис. 2.1. Ускоряющая структура для частиц со скоростью, равной скорости света

65

В основе рассмотрения высокочастотных свойств сверхпроводящих ускоряющих структур лежит ряд следующих исходных положений.

Запасенные электрическое и магнитное поля меняются во времени гармонически. Уравнения Максвелла для гармонического случая, без потерь и без свободных зарядов в объеме записываются в виде:

Граничные условия на проводящей поверхности записываются

то есть электрические силовые линии всегда перпендикулярны к поверхности резонатора, а магнитные силовые линии всегда параллельны поверхности.

Поскольку рассматриваемые резонаторы имеют цилиндрическую форму и симметричны, то используем цилиндрическую систему координат r, ϕ , z.

В ускорителях распределение поля должно иметь значительную составляющую электрического поля вдоль траектории частиц. Это гарантирует, при соответствующем фазировании, максимальный обмен энергией между резонатором и пучком.

Монопольные виды колебаний (моды) Е0ip имеют большую составляющую поля Еz на оси. Поля этих мод не зависят от угла ϕ :

Немонопольные волны высших типов (ВВТ) имеют на оси симметрии Еz=0. Их поля зависят от угла ϕ .

Уравнения Максвелла и граничные условия для электрического и магнитного полей E и H позволяют получить уравнение Гельмгольца, которое является задачей на собственные значения.

Для поля H (r,z) монопольных мод это уравнение записывается в виде

66

При решении уравнения Гельмгольца получается бесконечное число Е0ip решений. Все моды определяются частотой ω n и поля-

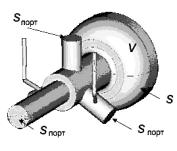
Величина потерь энергии в металлической стенке определяется собственной добротностью Q0, а потери энергии из-за излучения через открытые порты определяются внешней добротностью Qвн (см.

рис. 2.2).

Связь собственной и внешней добротности с нагруженной добротностью Qн,n записывается в виде

67

При описании свойств сверхпроводящих резонаторов вводится понятие меры потерь энергии в металлической стенке для поверхностного сопротивления RS,n = 1 Ом [2.6, 2.7]:

S

Этот параметр есть отношение запасенной энергии в объеме резонатора к интегралу Hn2 на металлической поверхности.

Взаимодействие пучка с резонатором, которое ускоряет пучок или доускоряет (как в линейном ускорителе с рекуперацией энергии ERL), или возбуждает волны высших типов, может быть описано как в частотной области (frequency domain – FD), так и во временной области (time domain – TD).

Для характеристики эффективности ускоряющих резонаторов вводится понятие эффективного шунтового сопротивления на единицу длины rш.эф, которое учитывает изменение амплитуды напряженности поля за время пролета частицей резонатора [2.8]:

где Vn – действительное напряжение, которое «видит» частица при пролете резонатора со скоростью v=β с, l – длина резонатора. Очевидно, Vn = ∆ W e , где e – заряд электрона, ∆ W– прирост энергии, причем

где t=z/v–t0; t0 – момент влета частицы в резонатор. Перепишем это выражение, умножив обе части на частоту: ω t = ω z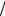v − ψ 0 ,

где ψ 0 – фаза влета частицы.

Теперь выражение (2.16) принимает вид:

68

Итак,

0

Или полное эффективное шунтовое сопротивление

Rш.эф=rш.эф l.

Отношение шунтового сопротивления к добротности (Rш.эф/Q)n, как «мера» обмена энергией между точечной частицей и n-м видом колебаний, представляется в виде

Для ускоряющих видов колебаний часто используют произве-

дение Gуск(Rш.эф/Q)уск как «меру» мощности P, рассеянной в металлической стенке при данном ускоряющем напряжении Vуск и дан-

ном поверхностном сопротивлении Rс:

Величина сопротивления Rс связана с качеством поверхности. Очевидно есть большие возможности его уменьшения и, тем самым, уменьшения рассеянной мощности, уменьшения потерь при криогенной температуре.

Параметр Gуск(Rш.эф зависит от геометрии ячейки. Здесь есть возможности его улучшения соответствующим выбором геометрии ускоряющей ячейки.

В соответствии с фундаментальной теоремой нагрузки пучком индуцируемое напряжение Vq, которое воздействует на частицу, пролетающую через резонатор, равно половине индуцированного напряжения Vb, которое частица оставляет в резонаторе, то есть

Для каждого вида колебаний резонатора вводится параметр потерь k=1/4α так, чтобы потери энергии точечного заряда q в пустом

Напряжение, индуцированное в резонаторе точечным зарядом q, будет

69

а напряжение, индуцированное на этой же моде и которое «видит» сам заряд, будет

Энергию, запасенную в резонаторе, индуцированную точечным зарядом, можно выразить как

так что параметр потерь

Принято выражать параметр k в таком виде, чтобы можно было оценить его по электродинамическим характеристикам моды резонатора, которые рассчитываются по стандартным программам. Отождествляем напряжение Vb как напряжение V0T, которое включает пролетный фактор. Используя выражения для эффективного погонного шунтового сопротивления (2.12) и собственной добротности (2.8), получим для коэффициента потерь

Когда заряд пролетает резонатор, он индуцирует напряжение Vbn = 2kn q для каждой моды n. Общее индуцированное напряжение

является суммой индуцированных напряжений на каждой моде. Обычно ускоряющей моде приписывают обозначение n=0. Другие моды, которые называют высшими (волнами высших типов, ВВТ), имеют значения n>0. Когда заряд q пролетает первоначально невозбужденный резонатор, полное наведенное напряжение VbT будет суммой напряжений основной и высших мод, то есть

Обозначим коэффициент увеличения для волн высших типов в виде

∞

B = ∑ kn . (2.30)

n= 0 k0

70