ЛЕКЦИИ ЧАСТЬ I

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей

Допускаемая сила при расчете по разрушающим нагрузкам, определяется путем деления предельного усилия на заданный коэффициент запаса

F = Fku .

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей

5 НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ В ТОЧКЕ ТВЕРДОГО ТЕЛА

5.1 ПОНЯТИЕ О НАПРЯЖЕННОМ СОСТОЯНИИ В ТОЧКЕ ТЕЛА

Напряженным состоянием в точке твердого деформируемого тела называют совокупность напряжений, действующих по всевозможным площадкам, проведенным через эту точку. В общем случае в теле напряженное состояние неоднородно − оно меняется от точки к точке и поэтому по любому сечению этого тела A напряжения распределены неравномерно. Для изучения напряженного состояния в какой-либо точке K мысленно вырезают в ее окрестности параллелепипед со сторонами dx, dy и dz (рис. 5.1). Ввиду малости элементарного параллелепипеда можно считать, что напряжения по его граням и по любым наклонным сечениям распределены равномерно. Напряжения на гранях параллелепипеда при этом считаются заданными, а напряжения, действующие в его наклонных площадках, определяют с помощью метода сечений, т.е. из условий равновесия отсеченной части параллелепипеда.

Рисунок 5.1 – Элементарный объем в окрестности точки тела

В любой точке нагруженного тела всегда можно выделить элементарный параллелепипед, ориентированный так, что все его грани будут свободны от касательных напряжений. При этом различают линейное, плоское и объемное напряженные состояния в точке (рис. 5.2). Линейное напряженное состояние, например, испытывают точки бруса при центральном растяжении или сжатии. Плоское напряженное состояние наиболее часто встречается в задачах сопротивления материалов. Его характерным признаком является отсутствие каких-либо напряжений на двух параллельных гранях параллелепипеда. Когда по всем граням элементарного объема действуют напряжения, то говорят об объемном напряженном состоянии в точке тела.

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей

Иногда указанные виды напряженных состояний называют соответственно одноосным, двухосным или трехосным.

Рисунок 5.2 – Виды напряженного состояния

а) линейное напряженное состояние; б) плоское напряженное состояние; в) объемное напряженное состояние.

5.2ОБЪЕМНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ

5.2.1ЗАКОН ПАРНОСТИ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЕЙ. ТЕНЗОР НАПРЯЖЕНИЙ

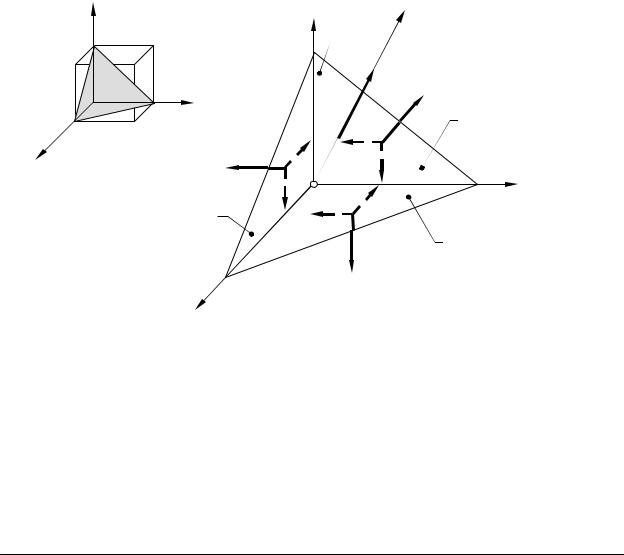
Вырежем элементарный объем в окрестности некоторой точки, принадлежащей деформируемому твердому телу. Оси координат совместим с центром элемента. В случае объемного напряженного состояния на гранях элементарного параллелепипеда в общем случае будут действовать напряжения, показанные на рис. 5.3a.

Рисунок 5.3 – Объемное напряженное состояние

Выше указывалось, что во всех точках элементарного объема напряженное состояние считается однородным. Поэтому одноименные напряже-

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей

ния на параллельных гранях показаны численно равными друг другу. Следует обратить внимание на индексы при обозначении напряжений. У касательного напряжения имеется два индекса, например τzx. Здесь первый индекс показывает, что данное касательное напряжение действует на площадке с нормалью, параллельной оси z, второй индекс обозначает, что вектор касательного напряжения параллелен оси x. Нормальное напряжение имеет только один индекс, который указывает, что вектор напряжения направлен вдоль соответствующей оси.

Примем следующее правило знаков для напряжений: растягивающее нормальное напряжение σ будем считать положительным, сжимающее − отрицательным. Знак касательных напряжений τ связан с направлениями осей координат: если внешняя нормаль данной площадки совпадает с направлением соответствующей координатной оси, то на этой площадке напряжение положительно, когда оно совпадает по направлению с соответствующей осью. Если же внешняя нормаль противоположна направлению оси, то направление τ положительно тогда, когда оно также противоположно соответствующей координатной оси. Это правило называют правилом внешней нормали.

При анализе плоского напряженного состояния в точке напряжения σx , σ y , σz , τxy , τyz и τzx считаются заданными и поэтому их называют исходными напряжениями. Поворачивая параллелепипед относительно координатных осей, можно получить такую его ориентацию, что все грани элементарного объема будут свободны от касательных напряжений. Нормальные напряжения, действующие по этим площадкам, будем называть главными напряжениями и обозначать σ1 , σ2 , σ3 соответственно (рис. 5.3б).

Приравнивая нулю сумму моментов всех сил относительно осей х, у и z, получим следующие равенства:

Соотношение (5.1) называется законом парности касательных напряжений:

на двух взаимно перпендикулярных площадках составляющие касательного напряжения, нормальные к линии пересечения площадок, равны по величине, а по направлению таковы, что стремятся повернуть элемент в противоположные стороны.

В общем случае объемного напряженного состояния в точке запишем напряжения, действующие по трем взаимно перпендикулярным площадкам в виде следующих матриц третьего порядка (5.2). Эта матрица носит название

тензора напряжений, а ее элементы называются компонентами тензора на-

пряжений. Понятие тензора является более общим, чем, например, понятие вектора. Оно часто встречается в математике, физике, механике. Из девяти компонент тензора напряжений в силу (5.1) различными могут быть только

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей

шесть. Для тензора характерным является закон, по которому преобразуются его компоненты при повороте осей координат.

5.2.2 ГЛАВНЫЕ НАПРЯЖЕНИЯ И ГЛАВНЫЕ ПЛОЩАДКИ

При объемном напряженном состоянии, меняя ориентировку осей и параллелепипеда, можно найти такое их положение, когда на всех гранях касательные напряжения будут равны нулю. Площадки, параллельные граням параллелепипеда, ориентированного указанным образом, называют главными площадками (рис. 5.3б). Действующие на них напряжения σ1 , σ2 , σ3 , как мы

уже знаем, называются главными напряжениями, а соответствующие им оси

− главными осями.

жения, действующие на произвольных наклонных площадках (рис. 5.4). Выделим из исходного параллелепипеда тетраэдр и составим условия его равновесия в виде сумм проекций всех действующих сил на оси координат.

Косинусы углов, образованных нормалью ν с осями х, у и z, обозначим соответственно l, т и п и будем в дальнейшем называть направляющими косинусами. Обозначим площадь наклонной грани dА, тогда площади других граней, лежащих в координатных плоскостях, будут соответственно равны:

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей

Для вычисления l, т и п, соответствующих одному из трех главных напряжений, необходимо значение этого главного напряжения подставить в (5.3) вместо величины σ. Совместное решение (5.3) и (5.4) даст искомые величины направляющих косинусов.

5.2.3 НАПРЯЖЕНИЯ НА ПРОИЗВОЛЬНО НАКЛОНЕННЫХ ПЛОЩАДКАХ

∑ν = 0 ; σn dAν −σ1dA1 cosα1 −σ2 dA2 cosα2 −σ3dA3 cosα3 = =σn dAν −σ1dAν cos2 α1 −σ2 dAν cos2 α2 −σ3 dAν cos2 α3 = 0 ,

отсюда

Так как нам заранее неизвестно направление касательного напряжения τп , то прежде найдем полное напряжение на наклонной площадке рп. Если в

пространстве построить многоугольник сил, действующих на тетраэдр, то вектор pnА будет диагональю параллелепипеда, у которого ребра соответственно равны σ1А1, σ2А2 и σ3А3, и поэтому

(pν Aν )2 = (σ1 A1 )2 + (σ2 A2 )2 + (σ3 A3 )2 .

Отсюда получим полное напряжение

Теперь можно определить касательное напряжение:

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей

5.2.4 ОКТАЭДРИЧЕСКИЕ НАПРЯЖЕНИЯ Площадки, равнонаклоненные к на-

IIправлениям трех главных напряжений, называется октаэдрическими, а действующие на ней напряжения — октаэдри-

ческими напряжениями. Указанные пло-

IIIщадки отсекают на осях I, II и III равные отрезки и образуют в пространстве вось-

По определению для октаэдрических площадок α1 =α2 =α3 и, следовательно,

При изучении вопросов прочности и пластичности тел общая деформация материала в окрестности точки подразделяется на деформации изменения объема и формы. Важное значение октаэдрических напряжений определяется тем, что с деформацией объема связано напряжение σokt , а с дефор-

мацией формы − τokt .

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей

5.2.5 ЗАКОН ГУКА ПРИ ОБЪЕМНОМ НАПРЯЖЕННОМ СОСТОЯНИИ

Рассмотрим твердое тело, находящееся в объемном напряженном состоянии. В окрестности некоторой точки тела вырежем элементарный объем (рис. 5.7). На гранях элементарного параллелепипеда не показаны касательные напряжения. При малых деформациях касательные напряжения вызывают только сдвиг прямоугольного элемента, не изменяя длины его сторон. Далее будем рассматривать лишь линейные деформации элемента.

σy

Рисунок 5.7 – Деформации элементарного объема в направлении оси ОХ

Найдем выражения для линейных деформаций εx , εy и εz через нормальные напряжения σx , σy и σz . Для этого воспользуемся принципом независимости действия сил. Суммарное относительное удлинение εx по направлению напряжения σx можно представить так:

εx = εxx +εxy +εxz ,

где εxx − продольная деформация в направлении оси ОХ, возникающая при действии на элемент только напряжения σx ;

εxy − поперечная деформация в направлении оси ОХ, возникающая при действии на элемент только напряжения σy ;

εxz − поперечная деформация в направлении оси ОХ, возникающая при действии на элемент только напряженияσz .

Используя выражения (4.4) и (4.6) получаем

εx = σЕx − μ σЕy − μ σЕz .

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей

Применяя подобные рассуждения к определению εy и εz , можем окон-

чательно записать формулу закона Гука при объемном напряженном состоя-

нии (обобщенный закон Гука) в следующем виде:

В этих формулах растягивающее напряжение записывается со знаком плюс, а сжимающее − со знаком минус.

5.2.6 ИЗМЕНЕНИЕ ОБЪЕМА МАТЕРИАЛА ПРИ ДЕФОРМАЦИИ

Обозначим размеры сторон элементарного параллелепипеда до деформации через dx, dy и dz (рис. 5.8). После деформации тела эти размеры будут

Рисунок 5.8 – Изменение объема элементарного параллелепипеда

Выполняя в полученном выражении перемножение величин, стоящих в скобках, получим