
ЛЕКЦИИ ЧАСТЬ I
.pdf
Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей
F O
х
у l l+ l
b |
|
|
b− b |
|
|
O |
|
|
h |
|
|
F |
h |
|
h− |
||
|
z
Рисунок 4.2 – Деформации призматического бруса при растяжении
При действии продольных сил первоначальная длина стержня l увеличивается на величину l . Удлинение стержня l называется абсолютной продольной деформацией, которая измеряется в единицах длины. Отношение первоначальной длины стержня l к величине l называется относительной продольной деформацией:
εz = |
l . |
(4.2) |
|
l |
|
Высота и ширина поперечного сечения стержня уменьшаются на |
h и |
|
b соответственно. Эти величины называются абсолютными поперечными деформациями. Отношение абсолютной поперечной деформации к первоначальному размеру поперечного сечения стержня называется относительной
поперечной деформацией: |
|
|
|
|
|
εх = − |
b |
и |
εy = − |
h . |
(4.3) |
|
b |
|
|
h |
|
Здесь знак «−»поставлен потому, что поперечные размеры стержня при растяжении уменьшаются. Деформации εz , εх и εу называются также линейны-
ми деформациями и являются безразмерными величинами. Для всех изотропных материалов εх =εу .
Абсолютное значение отношения относительной поперечной деформации к относительной продольной деформации в области упругих деформа-
ций называется коэффициентом Пуассона:
© Кафедра сопротивления материалов и строительной механики КубГТУ |
41 |

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей
μ = |
|
εx |
|
= |
|
εy |
|
(4.4) |
|||
|
|
|
|
. |
|||||||
|
ε |
|
|
||||||||
|
|
z |
|
|
|
ε |
z |
|
|
||
Для всех известных в природе материалов коэффициент Пуассона изменяется в следующих пределах 0 ≤ μ ≤ 0,5.
Коэффициент Пуассона является безразмерной величиной и определяется экспериментальным путем. Коэффициента μ и является одной из важнейших физико-механических характеристик материала. Этот коэффициент носит имя французского ученого Симона Дени Пуассона (1781−1840), кото-
рый впервые ввел его в теорию сопротивления материалов. Фундаментальная зависимость между силами и вызываемыми ими пе-
ремещениями была впервые открыта английским ученым Робертом Гуком в конце XVII в. Результаты своих многочисленных экспериментов при изучении поведения стальной проволоки и пружин, нагруженных грузами, Гук опубликовал в 1676 г. Впервые закон Гука был записан в виде анаграммы из латинских букв. Только через три года, убедившись в справедливости своих выводов, Гук расшифровал анаграмму – «Ut tension sic vis» («Каково удлинение, такова сила»). Таким образом, Гук установил прямо пропорциональную зависимость образца от растягивающей силы.
Вначале XIX английский ученый Томас Юнг (1773−1829) установил, что для каждого материала существует постоянная величина, характеризующая его способность сопротивляться действию внешних нагрузок. Следует отметить, что Юнг впервые указал на то, что закон Гука справедлив только в области упругих деформаций.
В1822 г. французский математик Огюстен Луи Коши (1789−1857) сформулировал и ввел в научную литературу такие понятия, как «напряжения» и «деформация». Окончательный шаг в формировании закона Гука в его современном виде был сделан французским инженером и ученым Мари
Анри Навье (1785−1836). В 1826 г. он дал определение модуля упругости как отношение нагрузки, приходящейся на единицу площади поперечного сечения, к произведенному ею относительному удлинению:
E = |
σ . |
(4.5) |
|
ε |
|
Величина E называется модулем упругости первого рода или модулем Юнга. Модуль упругости является физико-механической постоянной материала и измеряется в Па (Н/м2). Таким образом, закон Гука записывается в виде следующей формулы
σ = Еε . |
(4.6) |
© Кафедра сопротивления материалов и строительной механики КубГТУ |
42 |

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей
Подставляя в формулу (4.6) выражения (4.1) и (4.2), получаем еще одну форму записи закона Гука, наиболее близкую к его первоначальной формулировке
l = |
Nz l |
. |
(4.7) |
|
|||
|
EA |
|
|
Величина EA называется жесткостью стержня при одноосном растяжении или сжатии.
Физико-механические характеристики Е и μ для различных материалов приведены в табл 4.1.
ФИЗИКО-МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ
|
|
|
|
|
|
Таблица 4.1 |
|
|
|
||||
Наименование |
Модуль упругости |
Коэффициент |
||||
материалов |
первого рода Е (МПа) |
Пуассона μ |
||||
Алюминиевые сплавы |
0,72 105 |
|
0,26−0,36 |
|||
Бетон |
(0,15−0,23) 105 |
0,16−0,18 |
||||
Известняк |
0,49 105 |
|
− |
|||
Медь |
(1,00−1,3) 105 |
0,31−0,34 |
||||
Мрамор |
0,42 105 |
|
− |
|||
Песчаник |
0,18 105 |
|
− |
|||
Пробка |
− |
|
|
|
|
0 |
Резина |
0,00008 |
|
10 |
5 |
0,50 |
|
|
|
|
||||
Сталь легированная |
2,1 105 |
|
0,25−0,30 |
|||
Сталь углеродистая |
(2,0−2,1) 105 |
0,24−0,28 |
||||
Стекло |
|
|
|
5 |
|
0,25 |
0,56 10 |
|
|
|
|||
Чугун |
(1,15−1,6) 105 |
0,23−0,27 |
||||
4.3 НАПРЯЖЕНИЯ В СЕЧЕНИЯХ, НАКЛОННЫХ К ОСИ СТЕРЖНЯ, ПРИ РАСТЯЖЕНИИ ИЛИ СЖАТИИ
Рассечем растянутый стержень наклонной плоскостью. Угол наклона этой плоскости к оси стержня α (рис. 4.3). Рассмотрим равновесие левой отсеченной части стержня. Площадь наклонного сечения стержня Aα можно
выразить через площадь его поперечного сечения: Aα = A / sinα .
Из условия равновесия отсеченной части легко установить, что равнодействующая внутренних сил в наклонном сечении R = F . Разложим эту силу на две составляющие: нормальную силу Nα = R sinα = F sinα и касатель-
ное усилие Tα = R cosα = F cosα . Нормальные напряжения в нормальном се-
© Кафедра сопротивления материалов и строительной механики КубГТУ |
43 |

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей
чении стержня равны σ = N A . Предположим, что нормальные и касательные напряжения равномерно распределены по наклонному сечению, отсюда
A . Предположим, что нормальные и касательные напряжения равномерно распределены по наклонному сечению, отсюда
|
|
σα = |
|
Nα |
|
= |
|
F sinα |
= |
F sin2 |
α =σ sin2 α ; |
|
(4.8) |
||||||||
|
|
|
Aα |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
A / sinα |
A |
|
|
|
|
|
|
|||||
|
τα |
= |
Tα |
|
= |
|
F cosα |
= F sinα cosα = σ sin 2α . |
|
(4.9) |
|||||||||||
|
Aα |
|
A / sinα |
|
|||||||||||||||||
|
|
|
|
|
|
|
A |
|
|
|
2 |
|
|
|
|||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из полученных фор- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мул видно, что в попереч- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
ных сечениях растянутого |
|||||||
x |
y |
|
|
|
|
|
|
|
|
|
|
|
стержня (α = 90°) |
нор- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мальные напряжения дос- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
тигают |
наибольших |
зна- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
чений |
( sinα =1,0 ), |
а ка- |
|||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
сательные напряжения от- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Nα |
|
|
|
|
|
сутствуют ( sin 2α = 0 ) |
||||
x |
y |
|
|
|
A |
α |
|
|
|
|
|
|
|
|
σα max |
=σ . |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
α |
|
|
|
R |
|
|
|
|
|
Наибольшие |
касательные |
||||
|
|
|
|
|
|
|
|
Tα |
|
z |
|
|
|
напряжения возникают на |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
площадках, |
наклоненных |
||||
|
Рисунок 4.3 – Усилия в наклонном сечении |
|
|||||||||||||||||||
|
|
под углом 45° к оси бруса. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
На этих площадках нормальные напряжения равны касательным: |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
τα max |
=σα |
= |
1 σ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Нормальные и касательные напряжения в площадках, параллельных оси бруса (α = 0°), равны нулю.
4.4НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРЯМОГО СТЕРЖНЯ
СУЧЕТОМ СОБСТВЕННОГО ВЕСА МАТЕРИАЛА
Рассмотрим растяжение заделанного верхним концом прямолинейного призматического стержня под действием собственного веса (рис. 4.4). Интенсивность распределенной нагрузки, приведенной к оси стержня
p = Aγ ,
где γ − объемный вес материала стержня.
Проведем сечение на расстоянии z от заделанного конца стержня. Продольная сила в рассматриваемом сечении равна
© Кафедра сопротивления материалов и строительной механики КубГТУ |
44 |

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей
|
|
|
|
γl |
0 |
|
|
|
|
|
|
|
l |
l |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Nz = ∫pdz =∫Aγdz =Aγ(l − z). |
|
|||||||||||||
|
|
|
A |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
z |
z |
|
|
|
|
|
|||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
+ |
|
|
|
|
|
|
Напряжение в этом сечении найдем |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
по формуле: |
|
|
|
|
|
|
|||||
l |
|
|
|
|
|
|
|
|
|
σz = |
Nz |
= |
Aγ(l − z) |
=γ(l − z). |
(4.10) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A |
A |
|
|
|
|
|
||||
|
p |
|
|
|
|
|
|
|
|
|
|
Нормальные |
|
напряжения |
от |
|||||||
|
|
|
|
|
|
+ |
|
|
|
|
действия собственного веса стержня |
|||||||||||
|
|
|
|
|
|
|
|
γl2 /2E |
изменяются |
по линейному |
закону |
|||||||||||
|
|
|
|
|
|
|
|
(рис. 4.4б). На свободном конце |
||||||||||||||
|
a) |
|
|
0 б) |
в) |
|
стержня при |
z = l |
|
напряжения рав- |
||||||||||||
|
|
z |
|
|
|
|
|
ны нулю, а в заделке при |
z = 0 |
их |
||||||||||||
Рисунок 4.4 – Напряжения и удлинения |
значение равно σz |
=γl . |
|
|
|
|||||||||||||||||
стержня от собственного веса |
|
|
Найдем удлинение |
в |
произ- |
|||||||||||||||||
а) расчетная схема стержня; |
|
|
||||||||||||||||||||
|
вольном сечении стержня от дейст- |
|||||||||||||||||||||
б) эпюра напряжений σz ; |
|
|||||||||||||||||||||
|
вия собственного веса с помощью |
|||||||||||||||||||||
в) эпюра удлинений |
lz . |
|
||||||||||||||||||||
|
формулы (4.7) |
|
|
|
|
|
||||||||||||||||
|
|
|
|
lz = ∫z |
Nz dz |
= |
1 |
∫z |
Aγ(l − z)dz = |
γ |
z(2l − z). |
|
(4.11) |
|||||||||
|
|
EA |
EA |
2E |
|
|||||||||||||||||
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, удлинения стержня изменяются по квадратичному закону. На свободном конце стержня при z = l удлинения достигают максимальной
величины lmax = γl 2  2E , а в заделке при z = 0 равны нулю (рис. 4.4в).
2E , а в заделке при z = 0 равны нулю (рис. 4.4в).
Итак, мы установили, что в призматических стержнях напряжения от собственного веса меняются по длине стержня. Изменяя площадь поперечного сечения по длине, можно добиться того, что во всех поперечных сечениях стержня нормальные напряжения будут постоянными. Такой стержень называют стержнем равного сопротивления при растяжении или сжатии. Установим закон изменения площади поперечного сечения стержня равного сопротивления, изображенного на рис. 4.5 так, чтобы в любом сечении напряжения равнялись заданной величине σ . Площадь верхнего поперечного сечения Аo определяется по формуле (4.1):
σ |
|
= |
F |
; |
A = |
F |
. |
|
|
A |
|
||||||
|
0 |
|
|
0 |
σ |
0 |
|
|
|
|
|
0 |
|
|
|
|
|
На расстоянии близкими сечениями сечения элемента Аz,
няγAz dz .
z от верхнего конца стержня двумя бесконечно вырежем его элемент длиной dz. Площадь верхнего нижнего Аz + dАz. Вес выделенного элемента стерж-
© Кафедра сопротивления материалов и строительной механики КубГТУ |
45 |

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей
F 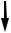 A0
A0
|
z |
l |
Az |
|
dz |
|
Az+d Az |
|
p |
z
Рисунок 4.5 – Брус равного сопротивления
Исходя из определения стержня равного сопротивления приращение площади dАz должно быть таково, чтобы воспринять приращение силы dFz, равное весу бесконечно малого элемента, т.е.
σ0 = dFz |
= γAz dz или |
dAz |
= γdz . |
||
dAz |
dAz |
|
|
Az |
σ0 |
Интегрируя полученное |
дифференциальное |
||||
уравнение, имеем |
|
|
|
|
|
|
ln A +C = |
γz |
. |
|
|
|
|
|
|||
|
z |
σ0 |
|
|
|
|
|
|
|
|
|
Постоянную интегрирования С находим из |
|||||
граничного условия: при z = 0 |
Az |
= A0 . Отсюда |
|||
ln A0 + C = 0 и C = −ln A0 .
Подставляя значение постоянной интегрирования C , получаем
ln |
Az |
= |
γz |
|
||||||
А |
σ |
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
|
|
|
|
|
|
или после потенцирования |
|
|
|
|
|
|
|
|
|
|
|
Az |
|
|
γz |
|
|
|
|
|
|
|
= е |
σ0 |
, |
|
|
|||||
|
А |
|
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
0 |
|
|
|
|
|
|
|
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γz |
|
||
|
A = А е |
σ0 |
. |
(4.12) |
||||||
|
|
z |
|
|
0 |
|
|
|
|
|
Следует заметить, что рациональный закон изменения очертания стержня зависит от действующей нагрузки.
4.5 ИСПЫТАНИЯ МАТЕРИАЛОВ НА РАСТЯЖЕНИЕ И СЖАТИЕ
При проектировании строительных конструкций, машин и механизмов инженеру необходимо знать прочностные свойства материалов. Их можно получить путем механических испытаний стандартных образцов на соответствующих испытательных машинах. Остановимся на наиболее простых видах испытаний материалов – растяжении и сжатии.
© Кафедра сопротивления материалов и строительной механики КубГТУ |
46 |

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей |
|||||
|
|
|
|
1 |
– неподвижная траверса; |
|
|
|
|
2 |
– подвижная траверса; |
|
|
|
|
3 |
–станина подвижной траверсы; |
|
|
|
|
4 |
– диаграммный механизм; |
|
|
2 |
|
5 |
– верхний захват; |
|
|
|
6 |
– нижний захват; |
|
Зона испытаний |
|
|
|
7 |
– растягиваемый образец ; |
5 |
|
|
8 |
– сжимаемый образец; |
|
на растяжение |
|
|
|||
|
|
9 – рабочая жидкость; |
|||
|
7 |
6 |
|
10 – поршень; |
|
|
|
|
|
11 – рабочий цилиндр; |
|
|
|
|
1 |
12 – манометр; |
|
|
|
|
13 – насос |
||
|
|
|
|
||
|
|
|
|
|
4 |
|
8 |
|
|
|
|
|
|
|
|
3 |
12 |
Зона испытаний |
|
|
|
11 |
|
|
|
|
|
||
|
|
|
|
|
|
на сжатие |
|
|
|
|
|
|
|
|
|
|
13 |
|
10 |
9 |
|
|
|
Рисунок 4.6 – Принципиальная схема универсальной испытательной машины гидравлического типа
В зависимости от способа приложения нагрузки испытательные машины подразделяют на машины с гидравлическим и механическим приводом. Испытания на растяжение выполняют или на разрывных или на универсальных машинах. Передача усилий на образец осуществляется через захваты. Все машины оснащены устройством для автоматической записи в определенном масштабе графика зависимости между растягивающим усилием F и удлинением образца l . Этот график принято называть диаграммой растяжения. На рис. 4.6 изображена принципиальная схема универсальной испытательной машины гидравлического типа.
© Кафедра сопротивления материалов и строительной механики КубГТУ |
47 |

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей
Универсальные испытательные машины имеют две рабочие зоны, где выполняются испытания материалов на растяжение и сжатие. В гидравлических испытательных машинах продольная сила на образец 7, помещенный в захваты 5 и 6, передается от подвижной траверсы 2, которая поднимается за счет увеличения давления жидкости 9 в рабочем цилиндре 11. Изменение давления в рабочем цилиндре 11 создается насосом 13. Это давление передается на поршень 10 и передается на подвижную траверсу 2. Неподвижная траверса 1 металлическими стойками соединяется с неподвижным фундаментом и воспринимает силу от образца 7 через нижний захват 6. Показания силы определяются с помощью манометра 12. При испытаниях на сжатие образец 8 помещают между неподвижной траверсой 1 и станиной подвижной траверсы 3. Диаграммный механизм 4 предназначен для записи диаграммы разрушения. При вертикальном перемещении траверсы 2 барабан механизма 4 начинает вращаться, а изменение продольной силы вращении приводит к горизонтальному смещению пера самописца.
d 0
0
l0
l0
b0
h0
Рисунок 4.7 – Стандартные образцы для испытаний материалов на растяжение
Механические испытания проводятся в соответствии с ГОСТ 1497−84. Для испытаний на растяжение применяются цилиндрические или призматические образцы (рис. 4.7). Образцы имеют рабочую часть с начальной длиной l0 , на которой определяются удлинения, и утолщенные части с переходными
участками, предназначенные для закрепления их в захватах испытательной машины. Различают длинные образцы с соотношением l0  d0 =10 и короткие
d0 =10 и короткие
– с соотношением l0  d0 = 5 .
d0 = 5 .
Для испытаний металлов на сжатие обычно используют цилиндрические образцы с соотношением h0  d0 =1,5 −3,0 . Применение более длинных
d0 =1,5 −3,0 . Применение более длинных
образцов не допустимо, так как длинные образцы в процессе испытаний могут потерять устойчивость (рис. 4.8). Для испытаний неметаллических мате-
© Кафедра сопротивления материалов и строительной механики КубГТУ |
48 |

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей
риалов используют как призматические, так и кубические образцы. При испытаниях на сжатие возникает трение между поверхностью образца и плитами испытательной машины. Чтобы устранить влияние сил трения на результаты испытаний при сжатии, торцевые поверхности образца обычно смазывают машинным маслом.
d0 |
b0 |
a
a0
0 |
h |
a |
h |
||
|
0 |
|
a
Рисунок 4.8 – Стандартные образцы для испытаний материалов на сжатие
Испытания на сжатие осуществляют при помощи прессов или универсальных испытательных машин. При испытаниях материалов на сжатие получают график зависимости между сжимающим усилием F и относительной деформацией образца l − диаграмму сжатия.
4.6 ДИАГРАММА РАСТЯЖЕНИЯ ПЛАСТИЧНЫХ МАТЕРИАЛОВ
Испытания материалов проводятся для определения числовых характеристик, позволяющих оценить их прочность и пластичность. Эти характери-
стики обычно называют механическими характеристиками материала.
Испытательные машины строят диаграмму растяжения в координатах F − l . Для изучения свойств материалов удобнее пользоваться диаграммой растяжения, устанавливающей зависимость между нормальным напряжением σ и относительной деформацией ε . При построении этой диаграммы в образце вычисляются условные нормальные напряжения путем деления текущего значения нагрузки на первоначальную площадь σ = F A0 .
A0 .
Относительная деформация образца вычисляется путем деления абсолютного удлинения на его первоначальную длину ε = l l0 .
l0 .
Поэтому два указанных вида диаграммы растяжения (рис. 4.9) будут отличаться между собой только масштабом.
Рассмотрим диаграмму растяжения малоуглеродистой (пластичной) стали Ст. 3. На начальном участке диаграмма растяжения представляет со-
© Кафедра сопротивления материалов и строительной механики КубГТУ |
49 |

Молдаванов С.Ю. Курс лекций по сопротивлению материалов для строительных специальностей
бой наклонную прямую. В этих пределах напряжения увеличиваются пропорционально деформациям, т.е. соблюдается закон Гука.
F |
σ |
F |
F |
F |
u |
F |
|
|
|
u |
|
F |
σ |
σ |
σ |
σ |
σ |
||||
pr |
e |
y |
d |
pr |
e |
y |
d |
||
α |
|
|
|
|
α |
|
|
|
|
0 |
|
|
|
l |
0 |
|
|
|
ε |
|
|
|
|
|
|
|
|
||
Рисунок 4.9 – Диаграммы растяжения пластичного материала
Пределом пропорциональности σpr называется наибольшее напря-
жение, при котором справедлив закон Гука (для стали Ст. 3 σpr=210 МПа). Выше точки предела пропорциональности диаграмма искривляется, закон
Гука нарушается, деформации начинают расти быстрее роста напряжений. Достаточно близко к пределу упругости на криволинейном участке диаграммы можно отметить точку, соответствующую пределу упругости σе. Тангенс угла наклона диаграммы на этом участке относительно горизонтальной оси
численно равен модулю упругости материала tgα = σε = E .
Пределом упругости σе называется максимальное напряжение, которое может выдержать материал, не получая остаточной деформации при разгружении. Если через эту точку провести вертикальную линию, то левее этой линии на диаграмме будет зона упругих, а правее − зона упруго-пластиче- ских деформаций (так как там будут иметь место и упругие и пластические деформации).
Несколько выше диаграмма имеет горизонтальный (или почти горизонтальный) участок, которому соответствует предел текучести σу. На этом участке деформации растут без увеличения нагрузки − материал как бы «течет».
Пределом текучести σу называется напряжение, при котором деформации растут без увеличения нагрузки (для стали Ст. 3 σу=240 МПа). Горизонтальный участок диаграммы принято называть площадкой текучести.
Начиная с некоторого момента, дальнейшее увеличение деформаций связано с дальнейшим увеличением нагрузка. На этом участке диаграмма изменяется по плавной кривой, на которой имеется экстремум.
Пределом прочности σи или временным сопротивлением называется отношение наибольшей нагрузки, выдерживаемой образцом, к первоначальной площади его сечения. Предел прочности это некоторая условная харак-
© Кафедра сопротивления материалов и строительной механики КубГТУ |
50 |
