
Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)
.pdf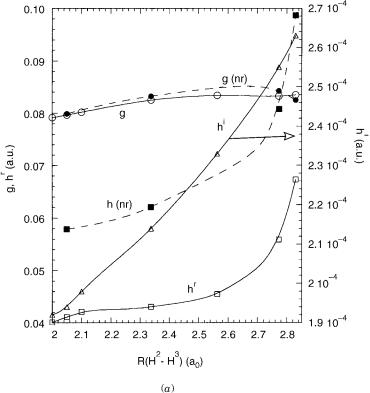
576 |
spiridoula matsika and david r. yarkony |
Figure 4 (Continued)
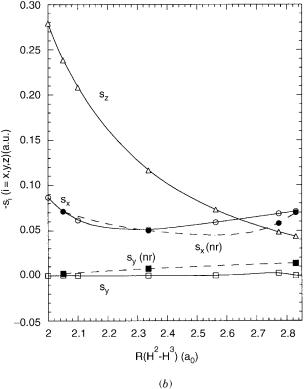
conical intersection dynamics has been discussed previously for nonrelativistic conical intersection [23,35]. For the conical intersections encountered heresx < hr;ijð sz > hi;ijÞ so that the cone is slightly (significantly) tilted in the xðzÞ direction. Such a topography faciliates the downward (upward) transitions from negative xðzÞ direction [23]. The linear coupling in the z direction, hi, is, however, quite small so that quadratic terms dominate except very close to the conical intersection. This will limit the role of this coordinate in inducing nonadiabatic transitions. It will be interesting to see how this changes as the size of the spin–orbit interaction increases.
E.Characterizing the Seam: Orthogonal g, hr, and hi
The conical parameters describe the topography of the conical intersection. The directions for g, hr, and hi relate the abstract x; y; z directions to actual molecular
conical intersections and the spin–orbit interaction |
577 |
Figure 4 (Continued)
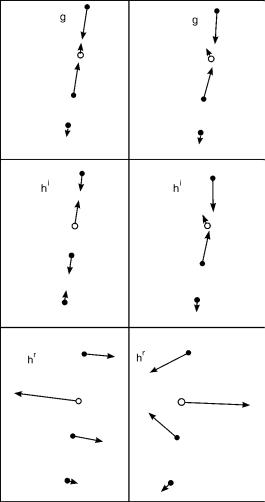
displacements. Figure 5 reports g; hr, and hi and their orthogonalized counter-
parts, |
~r |
, and |
~i |
at |
R |
x;ij |
(2.53), which is typical. The nascent |
r |
, and |
h |
i |
g~; h |
h |
|
g; h |
|
vectors are clearly not symmetry-adapted. The orthogonalization procedure removes this deficiency, with g and hi being symmetry preserving s displacements and hr being a p displacement.
|
Figure |
6 reports g~IJ |
, |
~IJ |
and |
the seam |
coordinates |
i |
; i ¼ 1–3 |
for |
||||||
R |
x;IJ |
|
|
h |
w |
|||||||||||
|
ð2:336Þ ¼ ð2:774; 1:873;IJ2:336Þ. |
Comparing Figures 5 and 6 illustrates |
||||||||||||||
|
|
|
ij |
|
~IJ |
|
|
~r;ij |
. These |
|||||||
the general observation that, g~ |
is parallel to g~ |
|
, and h |
is parallel to h |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~i;ij |
is a |
|
similiarities clearly depend on the use of the orthogonalized vectors. h |
||||||||||||||||
linear combination of two nonrelativistic symmetry preserving seam coordinates.
578 |
spiridoula matsika and david r. yarkony |
Figure 5. For Z ¼ 3, the vectors g, hr, and hi. Nascent (righthand column) and orthogonalized (left-hand column) results at Rx;ij(2.53). For orthogonal vectors
r |
¼ 0:0430; g ¼ 0:0825, and |
hi |
|
h |
¼ 0:000233. Vectors are scaled |
for visual clarity.
IV. THE FUTURE
In the nonrelativistic case much has been, and continues to be, learned about the outcome of nonadiabatic processes from the locus and topography of seams of conical intersection. It will now be possible to describe nonadiabatic processes driven by conical intersections, for which the spin–orbit interaction cannot be neglected, on the same footing that has been so useful in the nonrelativistic case. This fully adiabatic approach offers both conceptual and potential computational

conical intersections and the spin–orbit interaction |
579 |
Figure 6. For Z ¼ 2, the orthogonal vectors g; h and seam vectors wi; i ¼ 1–3. Orthogonal g and h
and three seam coordinates at Rx;IJ (2.33). g ¼ 0:0835; h ¼ 0:0514. Vectors are scaled for visual clarity.
advantages over approaches currently in use [36,37]. It will now be possible to address a key conceptual question: when does the relativistic description with intersections based on He, provide a better qualitative picture of a nonadiabatic process than a description with intersections based on H0. On the computational side, these new capabilities will enable a more rigorous approach whose computational utility increases with the size of the spin–orbit interaction. Diabatic bases deduced from a systematically improvable adiabatic representation will be possible.
580 |
spiridoula matsika and david r. yarkony |
At the present time, the solution of the electronic structure problem using full four component wave functions is far from routine [38]. In the future, as progress is made in this area, extension of the present approach to full four component wave functions can be expected.
In summary, the techniques outlined in this work represent the first step on a path that will lead to increased understanding of, and more accurate computational approaches for treating, nonadiabatic processes in which relativistic effects cannot be neglected.
Acknowledgments
This work was supported by the AFOSR, DoE Office of Basic Energy Sciences and the National Science Foundation.
References
1.D. R. Yarkony, J. Phys. Chem. A 105, 6277 (2001).
2.C. A. Mead, J. Chem. Phys. 70, 2276 (1979).
3.J. von Neumann and E. Wigner, Physik. Z. 30, 467 (1929).
4.M. R. Manaa and D. R. Yarkony, J. Chem. Phys. 93, 4473 (1990).
5.S. Xantheas, S. T. Elbert, and K. Ruedenberg, J. Chem. Phys. 93, 7519 (1990).
6.M. J. Bearpark, M. A. Robb, and H. B. Schlegel, Chem. Phys. Lett. 223, 269 (1994).
7.D. R. Yarkony, Rev. Mod. Phys. 68, 985 (1996).
8.S. Matsika and D. R. Yarkony, J. Chem. Phys. 115, 2038 (2001).
9.S. Matsika and D. R. Yarkony, J. Chem. Phys. 115, 5066 (2001).
10.S. Matsika and D. R. Yarkony, J. Chem. Phys. 116, 2825 (2002).
11.C. A. Mead, J. Chem. Phys. 78, 807 (1983).
12.D. R. Yarkony, J. Phys. Chem. A 101, 4263 (1997).
13.B. A. Hess and C. M. Marian, Relativistic Effects in the Calculation of the Electronic Energy, in
Computational Molecular Spectroscopy, P. Jensen and P. Bunker, eds., John Wiley & Sons, Inc., Chichester, UK, 2000, pp. 169–220.
14.L. I. Schiff, Quantum Mechanics, McGraw-Hill, New York, 1960.
15.M. Tinkham, Group Theory and Quantum Mechanics, McGraw–Hill, New York, 1964.
16.H. Kramers, Proc. Acad. Sci. Amsterdam 33, 959 (1930).
17.S. Matsika and D. R. Yarkony, J. Phys. Chem A, accepted for publication (2002).
18.D. R. Yarkony, J. Chem. Phys. 112, 2111 (2000).
19.D. R. Yarkony, J. Phys. Chem. A 105, 2642 (2001).
20.S. Matsika and D. R. Yarkony, J. Phys. Chem. A. 106, 2580 (2002).
21.D. R. Yarkony, Molec. Phys. 99, 1463 (2001).
22.M. V. Berry, Proc. R. Soc. London Ser. A 392, 45 (1984).
23.D. R. Yarkony, J. Chem. Phys. 114, 2601 (2001).
24.H. A. Bethe and E. E. Salpeter, Quantum Mechanics of One and Two Electron Atoms, Plenum/ Rosetta, New York, 1977.
25.S. R. Langhoff and C. W. Kern, Molecular Fine Structure, in Modern Theoretical Chemistry, H. F. Schaefer, ed., Plenum, New York, 1977, Vol. 4, p. 381.
conical intersections and the spin–orbit interaction |
581 |
26.D. R. Yarkony, Int. Reviews of Phys. Chem. 11, 195 (1992).
27.D. R. Yarkony, J. Chem. Phys. 89, 7324 (1988).
28.M. I. Lester, R. A. Loomis, R. L. Schwartz, and S. P. Walch, J. Phys. Chem. A 101, 9195 (1997).
29.D. R. Yarkony, J. Chem. Phys. 111, 6661 (1999).
30.B. C. Hoffman and D. R. Yarkony, J. Chem. Phys. 113, 10091 (2000).
31.B. H. Lengsfield and D. R. Yarkony, Nonadiabatic Interactions Between Potential Energy Surfaces: Theory and Applications, in State-Selected and State to State Ion-Molecule Reaction Dynamics: Part 2 Theory, M. Baer and C.-Y. Ng, eds., John Wiley & Sons, Inc., New York, 1992, Vol. 82, pp. 1–71.
32.M. R. Manaa and D. R. Yarkony, J. Chem. Phys. 99, 5251 (1993).
33.D. R. Yarkony, J. Chem. Phys. 97, 1838 (1992).
34.C. E. Moore, Atomic Energy Levels, Natl. Stand. Ref. Data Ser., Natl. Bur. Stand., U.S. GPO, Washington, DC, 1971.
35.G. J. Atchity, S. S. Xantheas, and K. Ruedenberg, J. Chem. Phys. 95, 1862 (1991).
36.A. L. Kaledin, M. C. Heaven, and K. Morokuma, Chem. Phys. Lett. 289, 110 (1998).
37.A. L. Kaledin, M. C. Heaven, and K. Morokuma, J. Chem. Phys. 114, 215 (2001).
38.K. G. Dyall and E. van Lenthe, J. Chem. Phys. 111, 1366 (1999).
584 |
miljenko peric´ and sigrid d. peyerimhoff |
Appendix A: Perturbative Handling of the Renner–Teller Effect and Spin–Orbit Coupling inElectronic States of Tetraatomic Molecules
Appendix B: Perturbative Handling of the Renner–Teller Effect and Spin–Orbit Coupling inElectronic States of Tetraatomic Molecules
Acknowledgments References
I.RENNER OR RENNER–TELLER?
It is not usual to begin a review with the discussion of its title; we find, however, that we have to do that in the present case. In the very representative book
Computational Molecular Spectroscopy [1], published last year, two papers written by eminent authors and devoted to the same subject, but with different titles, appeared back-to-back; one of them was entitled The Renner effect (Jensen and Bunker [2]), the title of the other was The Renner-Teller effect (Brown [3]). In his article, Brown explained this controversy in the following way: ‘‘The description of the vibrational levels for this pair of nearly degenerate potentials was first investigated in detail by Renner (1934) for a electronic state. However, the generalities of the problem had already been discussed by Herzberg and Teller in a preceding paper (1933). It is for this reason that some authors refer to vibronic coupling in a linear molecule as the Renner–Teller effect while the others prefer to call it simply the Renner effect. Both names are used in the literature to describe a single phenomenon. In this chapter, we follow Herzberg (1991) and refer to it as the Renner–Teller or R–T effect.’’
Formally, there was little reason to give Teller half of the credit for discovering such an important phenomenon. In the very extensive paper [4] referred to by Herzberg [5] as justification for the name ‘‘The Renner–Teller effect,’’ there are only a few sentences that discuss in general the consequences of the reduced symmetry in linear molecules upon bending on the reliability of the Born–Oppenheimer approximation [6] and thus on the vibrational structure of molecular spectra. Moreover, the first author of this paper is Herzberg himself. One can, of course, claim that this is the heart of the problem, but we do not believe that such a conclusion required too much intellectual effort of renowned theoreticians/spectroscopists who knew the works by Wigner, Born, and Oppenheimer. On the other hand, seldom has a completely new topic been elaborated on as thoroughly as in Renner’s paper [7]. We cannot agree with Jungen and Merer when they state in their excellent review [8] that ‘‘Renner’s original paper seems not to have received the recognition which we feel it deserves, possibly because it is in difficult German and in old notation.’’ We do not find Renner’s notation much different from that used today nor his German more difficult than Herzberg’s and Teller’s; in almost all papers devoted to this subject up to, say, the 1980s the name ‘‘Renner effect’’ had been used. The
renner–teller effect and spin–orbit coupling |
585 |
situation has gradually changed in the last two decades, which should at least partially be ascribed to Herzberg’s authority (By the way, Jungen and Merer were among the first to adopt the name ‘‘R–T effect.’’) We join here with those people who accept his recommendation, because he must have known the circumstances better than anybody else.
II.INTRODUCTION
The Renner–Teller effect (in the following text we shall use acronym R–T) arises when the potential energy surface of an electronic state spatially degenerate at the linear molecular geometry ( , , . . .) splits upon bending into two surfaces. From the group-theoretical point of view, this splitting is a consequence of reduction of the axial symmetry C1u, D1h upon bending to Cs, Cu, the latter two point groups possessing only one-dimensional (1D) irreducible representations. At small distortions of linearity the two (nondegenerate) electronic states, corresponding to these potential surfaces, lie close to each other, which manifests itself in a complicated vibrational and rotational structure of the corresponding spectra. The origin of the R–T effect can be interpreted in different terms: [8] (1) as a consequence of the electrostatic interaction between two components of an electronic state with a nonzero angular momentum; (2) as a coupling of two different electronic states through the electronic–rotational Coriolis interaction;
(3) from the quantum chemical standpoint, the R–T effect is a consequence of violation of validity of the Born–Oppenheimer approximation.
In his classical paper, Renner explicitly considered only one of several cases that differ from each other from a quantitative point of view, namely, that in which the molecular potential energy surfaces for both components of a state have the minimum at the linear geometry (we shall call this situation ‘‘weak R–T effect’’). The reason for his restriction to states was that he realized that the manifestation of the breakdown of the Born–Oppenheimer (BO) approximation seen in the spectral features would be most spectacular just in this case; at the same time this was the only situation for which closed formulas for vibronic (vibrational–electronic) energy levels could be derived by hand (in the framework of the perturbation theory). A generalization of his theory to the cases in which one or both of these potential surfaces has/have a minimum at a bent nuclear arrangement and to other degenerate electronic species is (at least from the conceptual point of view) more or less straightforward. It requires, however, other computational approaches (numerical, variational) to solve the corresponding equations.
As argued above, it is not Renner who should be blamed for his paper being forgotten for almost 25 years. The reason is that the experimentalists needed this much time to obtain the first spectrum showing the features predicted by him [9,10]. The effect that might have looked exotic in the 1930s has become one of
