Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)

We demonstrate this procedure by an explicit example—finding the H/allyl CI shown in Figure 18. In this case, any one of the three reaction channels may be used to begin the search, since all are phase inverting and therefore have an antiaromatic transition state. For example, the system is propagated along the reaction coordinate from CHDN to 1,3-CHDN, and the geometry and energy of the AATS of this reaction is computed. Next, vertical excitation leads to the first excited singlet state (S1) lying above this AATS. Subsequently, motion along is initiated along the phase-preserving coordinate connecting this point on S1 and the third anchor, BCE in this example, (which lies on S0). This procedure did indeed result in locating the conical intersection, as confirmed by calculating the energy gap between the two electronic states, while moving along.

As a check on the performance of the procedure, the formation of the three possible products on the ground-state potential surface was validated after the search for the conical intersection was concluded. Immediately following the crossing of the conical intersection, the system was allowed to relax to an energy minimum on the S0 surface. Removing all constraints led to one of the three anchors. The other two were sought by first ‘‘nudging’’ the atoms slightly in the direction of their geometry, and then letting the system find a minimum energy. The physical justification of the ‘‘nudging’’ is the ever present redistribution of energy on the ground-state surface (IVR). Recovery of the three anchors without encountering a barrier confirmed the location of the conical intersection in the loop and the validity of the process.

The energies of this CI and of the other ones calculated in this work are listed in Table III. The calculated CASSCF values of the energies of the two lowest electronically states are 9.0 eV (S1, vertical) and 10.3 eV (S2, vertical) [99]. They are considerably higher than the experimental ones, as noted for this method by other workers [65]. In all cases, the computed conical intersections lie at much lower energies than the excited state, and are easily accessible upon excitation to S1. In the case of the H/allyl CI, the validity confirmation process recovered the CHDN and 1,3-CHDN anchors. An attempt to approach the third anchor [BCE(I)] resulted instead in a biradical, shown in Figure 43. The biradical may be regarded as a resonance hybrid of two allyl-type biradicals.

TABLE III

The CASSCF(8,8)/DZV Energies of Some Stable Molecules and Conical Intersections Relevant to 1,4-cyclohexadiene (CHDN) Photochemistry (kcal/mole with respect to CHDN)

Note: In Hartree units, 231:84363

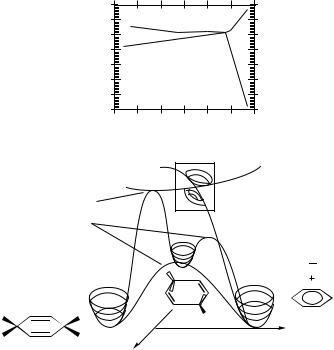
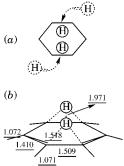
locality, the system was constrained to C2v symmetry, that is the rotational motion of the two hydrogen atoms forming the H2 molecules was frozen. It was found that the two surfaces (1A1 and 1A2, cf. Fig. 44) did cross at a certain geometry, representing a conical intersection, as expected from the phasechange rule. Some numerical results are reported in Figure 45. The approach to the conical intersection from the hexadiene side is much more gradual than from the benzene and H2 side. The geometry of this conical intersection, shown in Figure 45, is found to be similar to that of the AATS. In both, the C–C bonds have very similar values. The HH distance is much larger in the AATS, while the H2 center-of-mass distance to the carbon ring is larger in the conical intersection. The angle between the line connecting the two hydrogen atoms and the line connecting the two carbon atoms to which they were originally bonded changes due to the rotational motion of two hydrogen atoms with respect to the C6H6 fragment. It is 30 at both the AATS and at the conical intersection.

A2

A1

H H

X2

X1

Figure 44. The helicopter-type conical intersection for CHDN. Bottom: A cartoon showing the anchors and the conical intersection. Top: The calculated energies (kcal/mole) of S0 and S1 near the conical intersection.

Figure 45. The structure of the helicopter-type conical intersection of CHDN.

The two departing hydrogen atoms perform a complex motion from their initial positions to the conical intersection: contracting of the distance between them, rotation that brings them to the position above the center of the ring and increasing the distance between the center of mass (CM) of the H2 fragment and the carbon ring. The angular momentum created in this motion is the origin of the observed helicopter-type one. It may be traced to the participation of the isomerization reaction in the Longuet-Higgins loop encircling the conical intersection which induces the necessary angular momentum.

The two proposed conical intersections provide a model that is consistent with the experimental results on the CHDN system [60–64].

VII. COMPARISON WITH OTHER METHODS FOR LOCATING

CONICAL INTERSECTIONS

The method presented in this chapter is aimed mainly at providing information on the presence of conical intersections in large molecules, and helps in the calculation of their energies and structures. In this section, we review briefly some other procedures used to characterize conical intersections, and compare them with the present method.

The practical implementation of all schemes requires high-level quantum mechanical calculations. The major advances achieved in this field in the last two decades appear to be a major factor for the revival of interest in the subject. Several efficient computational methods are currently available for finding conical intersections in polyatomic systems and calculating their properties. The field is very active at the moment, and the prospects for further progress are very promising. Yet, it is still true, as summarized by Worth and Cederbaum [100]: The complete evaluation of potential energy surfaces is an impossible task for systems comprising more than a few atoms. Approximations have to be made— the different methods are distinguished mostly by the nature of the approximations.

The phase-change rule, also known as the Berry phase [101], the geometric phase effect [102,103] or the molecular Aharonov–Bohm effect [104–106], was used by several authors to verify that two near-by surfaces actually cross, and are not repelled apart. This point is of particular relevance for states of the same symmetry. The total electronic wave function and the total nuclear wave function of both the upper and the lower states change their phases upon being transported in a closed loop around a point of conical intersection. Any one of them may be used in the search for degeneracies.

Ruedenberg and co-workers [33,107], found by exact quantum chemical calculations a crossing point between the two lowest 1A1 states of ozone. They used the phase-change rule to verify that the electronic wave function changes its sign when transported in a closed loop around this point. This was done by considering the phase change of the dominant configurations of the ground-state wave functions. Initially, only C2v symmetry was considered, later, a complete seam of conical intersections was calculated [107].

Yarkoni [108] developed a computational method based on a perturbative approach [109,110]. He showed that in the near vicinity of a conical intersection, the Hamiltonian operator may be written as the sum a nonperturbed Hamiltonian H0 and a linear perturbative term. The expansion is made around a nuclear configuration Qx, at which an intersection between two electronic wave functions takes place. The task is to find out under what conditions there can be a crossing at a neighboring nuclear configuration Qy. The diagonal Hamiltonian matrix elements at Qy may be written as

where gIaðQxÞ ¼ cIðQxÞy½qHðQxÞ=qQa&cIðQxÞ ¼ ½dEIðQxÞ=qQa. gIaðQxÞ is thus the gradient of the energy along a small displacement dQ ¼ Sa½qQaqa&, with a

unit vector in the a direction.

In the special case of a triatomic system, gIaðQxÞ and hIJa ðQxÞ are onedimensional vectors, spanning the g–h plane. A closed loop in the g–h plane will change the sign of the electronic wave function. The degeneracy is preserved through first order provided dQ is restricted to motion along the g–hy plane, orthogonal to the g–h plane. The line connecting all degeneracies is the conical intersection seam. More generally, the conical intersection will be a 3N 8 dimensional surface.

The search for a conical intersection is based on the assumption that it is not feasible (or desirable) to characterize the entire surface of the conical intersection. Conical intersections of interest are those with energies accessible in chemical processes. Furthermore, it is desired to restrict the search to nuclear configurations of chemical interest. These constraints may be expressed mathematically (e.g., by Lagrange multiplier techniques). The Schro¨dinger equation is solved for the two states in question, and points of near crossing are checked by the phase change rule to verify whether the wave function indeed changes sign.

As shown by several authors, the sign ambiguity of the electronic wave function found by Longuet-Higgins near surface crossing in the adiabatic approximation (usual BO case) can be removed [102,103,111,112]. This is done by transforming to a diabatic framework, or representation, in which the Hamiltonian matrix is diagonalized near the conical intersection. The resulting diabatic states are coupled by potential coupling terms that can be calculated to a high degree of accuracy. It turns out that the number of important coupling terms is small, making the approximation practical. These coupling terms are closely related to the Jahn–Teller distortive modes, and in our model, to the coordinates connecting two anchors. Using this approach, Mebel et al. [113] showed that a conical intersection connecting the two low-lying states of C2H actually cross. The change in phase angle upon a complete loop around the point was calculated, using the coupling elements that were obtained by quantum calculations. Only when the loop enclosed a single conical intersection, the phase changed. When the loop enclosed two (or no) conical intersection, the phase did not change.

Robb, Bernardi, and Olivucci (RBO) [37] developed a method based on the idea that a conical intersection can be found if one moves in a plane defined by two vectors: x1 and x2, defined in the adiabatic basis of the molecular Hamiltonian H. The direction of x1 corresponds to the gradient difference

where E1 and E2 are the energies of the two electronic states in the BO approximation, and dq is a vector of nuclear displacement.

The direction of x2 is parallel to the direction g of the diabatic coupling matrix mentioned above

where 1 and 2 are the eigenfunctions of H. Note the formal similarity between the vectors x1 and x2 on one hand, and gIaðQxÞ and hIJa ðQxÞ [Eqs. (22–24)] on the other.

The system is propagated along the two vectors, until the separation between the two surfaces vanishes upon reaching the conical intersection geometry.

The practical application of the RBO method is helped by selecting the required coordinates based on chemical intuition or calculations. The original papers made use of the MMVB method [114]. The advantage of the MMVB method is that it is many orders of magnitude less expensive computationally than the currently high-level CASSCF method. A disadvantage is that it can only describe covalent states [114]. Minima on the conical intersection hypersurface are optimized using an algorithm developed by Bearpark et al. [115].

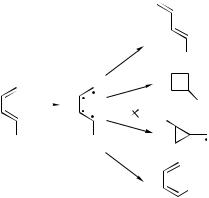
For the purpose of finding an efficient funnel connecting an excited electronic state and the ground state, the scrupulous distinction between ‘‘real’’ crossing and ‘‘near’’ crossing may be of theoretical importance only. In practice, the system will jump from one to other with similar effectiveness. Therefore, the conical intersection may be found by following the energy gap between the two states to a value close to zero. This method was used to analyze the photochemistry of a large number of molecules [9,37]. An example that lends itself to facile comparison with our method is the photochemistry of butadiene. [38,116]. Figure 46 summarizes their finding in a simple scheme. The conical intersection is presented as a tetraradical, which may stabilize by forming three types of bonds, depending on the electron pairs that form the bonds. This scheme is directly comparable to Figure 36. The upper reaction is an intraanchor reaction, the middle two are identical to those shown in Figure 36 and discussed in Section VI.A1. The reaction shown at the bottom of the scheme (trans–cis isomerization around one of the double bonds) would require, in our method, a different loop than the other three.

Wilsey and Houk [65] used the RBO method to find conical intersections in several olefins, including 1,4-cyclohexadiene (CHDN). This was done by using

chemical reactions coordinates to identify the gradient difference vector x1 and the non-adiabatic vector x2: When x1 corresponds to the motion leading to a trimethylene radical and x2 to the formation of the isomeric [1,3]-shift product, the H/allyl conical intersection is found (Section VI.B). When x1 corresponds to the motion leading to a C–C bond cleavage to form a diradical and x2 to the formation of the isomeric [1,3]-shift product, the vinyl–allyl conical intersection is found. This chemically oriented method is similar in spirit to our approach. Their strategy allows the finding of several conical intersections, by defining the gradient difference vector along a desired coordinate. Implicit in their approach is the idea that several conical intersections may be photochemically active for a specific system.

Ko¨ppel et al. [111] considered the so-called symmetry-allowed conical intersections. These intersections result from the allowed crossing of potential energy functions of two electronic states, which transform according to different irreducible representations of an appropriate symmetry group along a certain reaction coordinate. A further deformation, which lowers the symmetry, leads to interactions of the two states in first order in the displacement, converting the crossing to a conical intersection. The search for a conical interaction in this case is greatly helped by symmetry considerations, as has been recently demonstrated for malonaldehyde, pyrrol and chlorobenzene [7].

Worth and Cederbaum [100], propose to facilitate the search for finding a conical intersection if the two states have different symmetries: If they cross along a totally symmetric nuclear coordinate, then the crossing point is a conical intersection. Even this simplifying criterion leaves open a large number of possibilities in any real system. Therefore, Worth and Cederbaum base their search on large scale nuclear motions that have been identified experimentally to be important in the evolution of the system after photoexcitation.

A major motivation for the study of conical intersections is their assumed importance in the dynamics of photoexcited molecules. Molecular dynamics methods are often used for this purpose, based on available potential energy surfaces [118–121]. We briefly survey some methods designed to deal with relatively large molecules (>5 atoms). Several authors combine the potential energy surface calculations with dynamic simulations. A relatively straightforward approach is illustrated by the work of Ohmine and co-workers [6,122]. Ab initio calculations of the ground and excited potential surfaces of polyatomic molecules (ethylene and butadiene) were performed. Several specific nuclear motions were chosen to inspect their importance in inducing curve crossing. These included torsion, around C C and C–C bonds, bending, stretching and hydrogen-atom migration. The ab initio potentials were parametrized into an analytic form in order to solve the dynamic equations of motion. In this way, Ohmine was able to show that hydrogen migration is important in the radiationless decay of ethylene.

Ko¨ppel co-workers [121] developed a method that uses accurately calculated potential surfaces for dynamic simulations. The initially calculated adiabatic potential surfaces are diabatized, to avoid singularities that hamper dynamic calculations. Once the diabatic potential surfaces are determined, along with the off-diagonal coupling constants between them,wave-packet dynamics can be performed. The off-diagonal coupling constants are large along the conical intersection seam. The method was demonstrated for a triatomic molecules (O3, H2S, NO2 ), but is claimed to be suitable for larger systems [121].

Martinez and Ben-Nun [10,123] proposed a combined approach, in which the potential surfaces and the dynamics are treated on equal footing. In their AIMS method, ab initio quantum chemistry and nonadiabatic quantum dynamics are united. The electronic and nuclear Schro¨dinger equations are solved simultaneously, that is, the electronic structure problem is solved ‘‘on the fly’’ as dictated by the quantum mechanical nuclear dynamics. This method has recently been applied to ethylene. It was found that electronic excitation leads to an excited state that favors a twist of the two methylene groups to a perpendicular geometry, as well as pyramidalization of one of them. The combined effect lowers the energy of the excited state, and leads to several symmetry allowed crossings, the final one being to the ground state.

Our qualitative approach [40,41], which is based on the phase change theorem of Longuet-Higgins, considers spin pairing as the principal factor for locating conical intersections. We consider transitions from the first excited state to the ground-state, and form the loop on the ground-state surface. A given spin-paired system (anchor) may support many nuclear configurations on the ground state surface, but only one of them is usually at an energy minimum. As in all other methods mentioned above, the task is to find the two coordinates defining the loop that surrounds the conical intersection. We use for this purpose the reaction coordinates connecting the chosen anchors: A pair of reaction coordinates is sought, of which one is phase preserving (p) and the other phase inverting (i). There are many such pairs in a polyatomic molecule, which may be sorted out systematically. For any specific product, the reaction coordinate leading from the starting material is a natural choice. The phase change associated with this coordinate is well defined (either phase preserving or inverting). The second coordinate may be chosen from among all other reactions of the reactant, which may be found by considering all possible electron re-pairings. In practice, experiment and chemical intuition are used to facilitate and shorten the search. The three anchors of the loop, which are A—the reactant, B—the desired product, and C—another product, must form a phase inverting loop. This means that either all three reactions (A ! B, B ! C, and C ! A) are phase inverting, or that only one of them is. The loops formed are designated as i3and ip2, respectively. As shown in Section VI, the method is readily combined with high level quantum calculations for polyatomic systems.

Bornemann and Klessinger [124] used this approach in the analysis of the photoreactions of 2H-azirines. They implemented the method by calculating the groundand excited-state geometries using the CASSCF method, starting from previous MNDOC–CI results [125]. The coordinates along which the conical intersection was searched for were determined by the phase change rule. The main application of the method described in this paper is expected to be in the analysis of the photochemistry of large systems. The initial location of the conical intersection is not dependent on a numerical algorithm, but on basic principles. The assignment of spin pairing is a relatively straightforward job, and can be done systematically. In principle, the method relies mostly on ground-state species, whose properties are either experimentally accessible, or may be computed. The numerical application, briefly described in Section VI, is still being developed. Methods specializing in the calculations of ground-state properties are notably efficient and accurate. Currently, the properties of both the ground and the excited states need to be computed. In principle, as all conical intersections leading to the ground state are ‘‘points’’ on the groundstate surface, their properties may be calculated by methods specialized for this state.

VIII. IMPACT ON MOLECULAR PHOTOCHEMISTRY

AND FUTURE OUTLOOK

Conical intersections are important in molecular photochemistry, according to the current consensus, which is based on the combination of experimental and theoretical data. In this chapter, we tried to show that the location and approximate structure of conical intersections may be deduced by simple considerations of the changes in spin-pairing accompanying a reaction. We have also shown how these ideas may be put to practical computational application.

Chemists have developed several simple rules and methods that have helped to predict the course of photochemical reactions. In this section, we summarize some of these ideas and discuss their relation to the conical intersection model.

In distinction with thermal reactions, photochemical ones involve at least two potential surfaces. Attempts to understand them may be divided into two categories: those treating the ground and excited states separately, and those considering the coupling between the two as an essential ingredient. The first category analyzes photochemical reactions in terms of a kinetic mechanism, and seeks transition states and intermediates, in a manner that is commonly used for thermal reactions [126–128]. The rate-determining step, as a rule, is considered to be on the excited-state surface and the mechanism for the return from the excited to the ground state is not specified—it is assumed that the system will somehow find its way down. This approach, which views the photochemical process as a sequence of elementary reactions, each proceeding