10.138.

10.139.

10.8. Интегрирование тригонометрических функций.

1.Интегралы вида,,находятся с помощью тригонометрических формул:

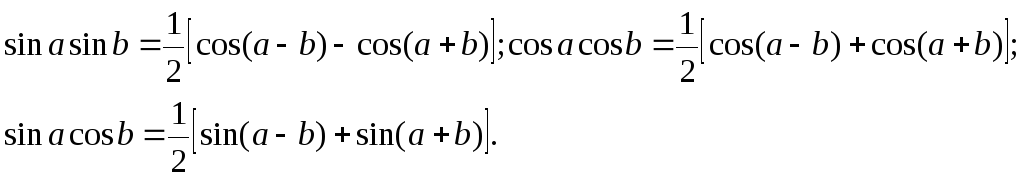
2.Интегралы вида, гдеnиm– четные числа, находятся с помощью формул:

.

Если хотя бы одно из чисел nиm – нечетное, то интеграл находим непосредственно, отделяя от нечетной степени один множитель и вводя новую переменную. В частности, еслиm=2k+1, то

3.Интегралы видагдеR– рациональная функция оти, приводятся к интегралам от рациональных функций новой переменной с помощью подстановки, при этом.

Если то целесообразно применить подстановку, при этом

1 .Найти интеграл

Так как то

2.Найти интеграл.

Запишем, что Тогда

(А)

Применяя подстановку , тогда, получим

Возвращаясь к старой переменной, получим окончательно

Собственно говоря, для вычисления интеграла (А) никакой подстановки не требуется, так как формула

позволяет сразу написать ответ. Из (А) следует, что

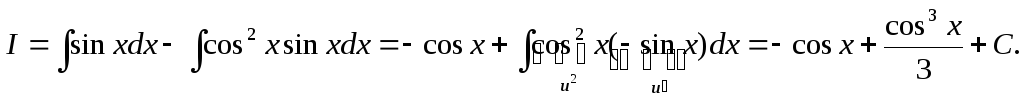
3.Найти

Применим универсальную тригонометрическую подстановку:

Поэтому

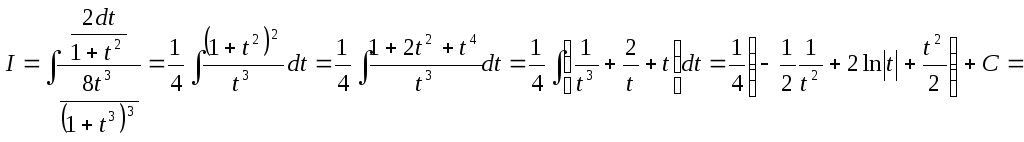Возвращаясь к старой переменной: заменяяна

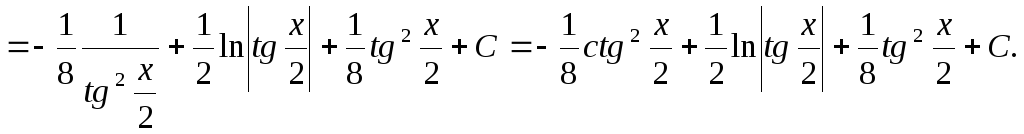
4.Найти интеграл

Подынтегральная функция не меняется от замены нана, т.е.

Применяя подстановку . Так как при этом

то

Следовательно,

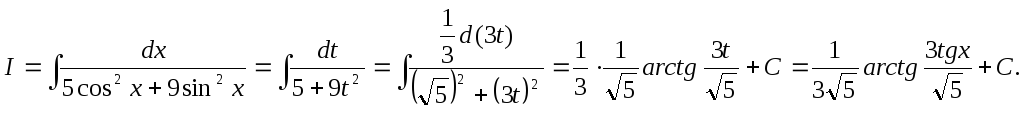
Найти интегралы:

10.146.10.147.10.148.

10.149.10.150.10.151.

10.152.10.153.10.154.

10.155.10.156.10.157.

10.158.10.159.10.160.

10.9. Интегрирование некоторых иррациональных функций.

1.Интегралы вида

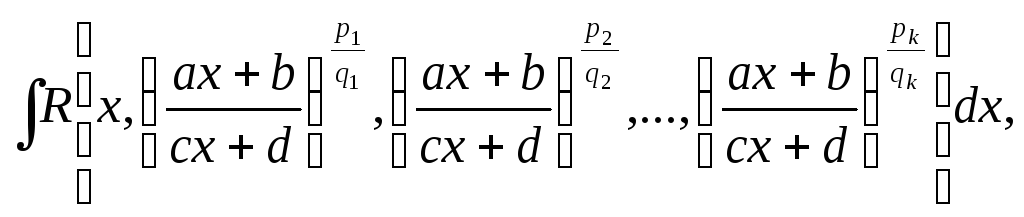(32)

где R– рациональная функция и- целые числа, находятся с помощью подстановки, гдеn– наименьшее общее кратное чисел.

2.Интеграл от дифференциального бинома, т.е. интеграл

,

где m, n, p–рациональные числа,a и b– постоянные, отличные от нуля; сводится к интегралу от рациональной функции в трех случаях:

1. когда p– целое число, - разложением на слагаемые по формулам бинома Ньютона;

2. когда 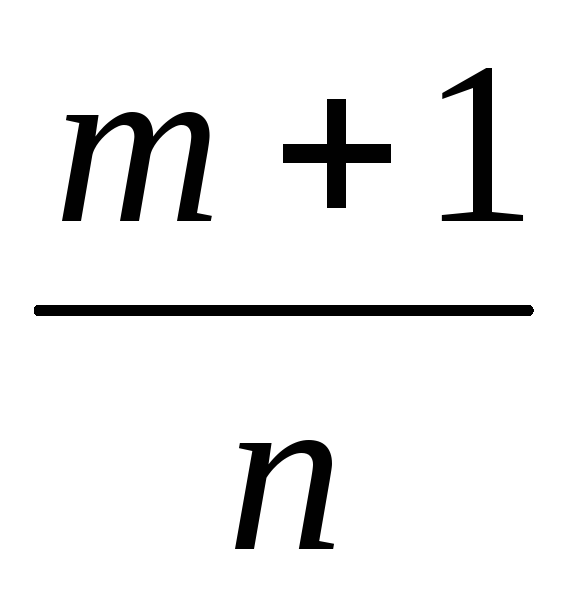– целое число, - подстановкой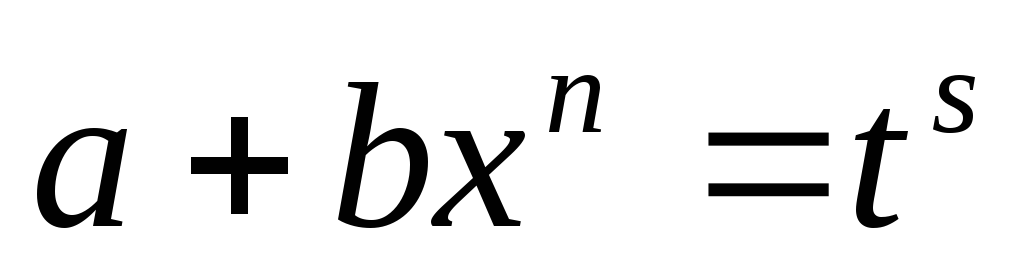, гдеs- знаменатель дробиp;

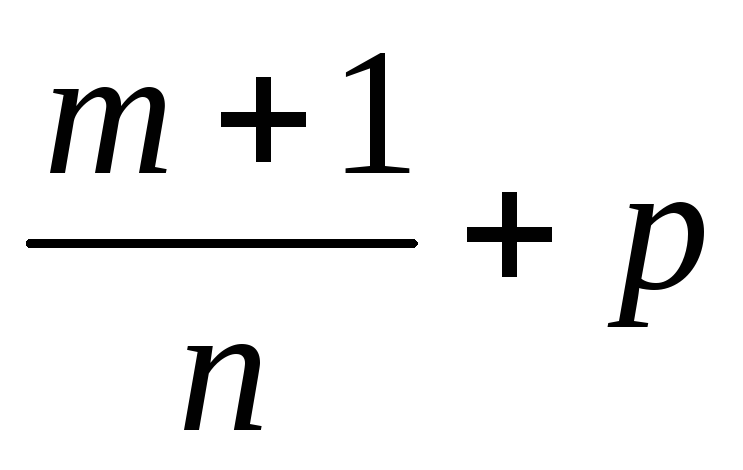3. когда - целое число, - подстановкой.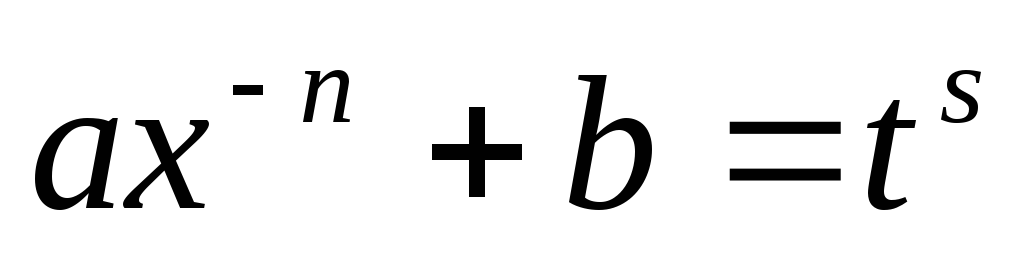

1. Найти интеграл

Это интеграл типа (32), для которого (т.е.),,,, общий знаменатель всех дробей равен 6, поэтому применим подстановку(она дает возможность освободиться от всех радикалов).

Поскольку , то

Следовательно,

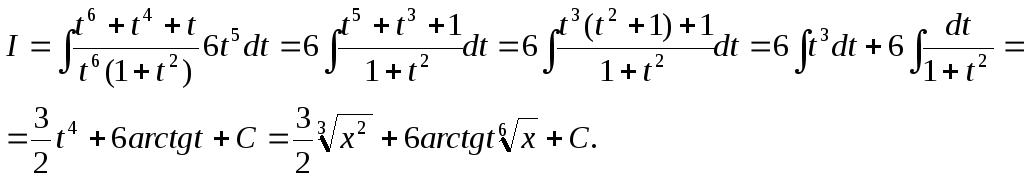
2.Найти.

Перепишем интеграл в виде

получим

Составим выражение 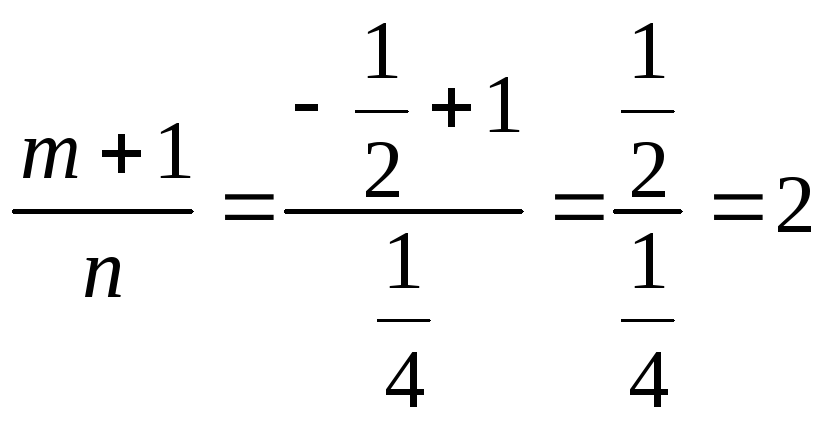- целое число.

Следовательно, здесь мы имеем второй случай интегрируемости. Подстановка запишется так,

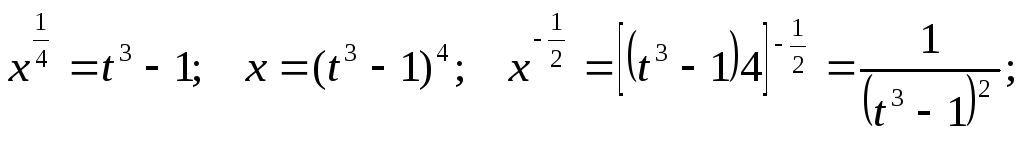
Поэтому

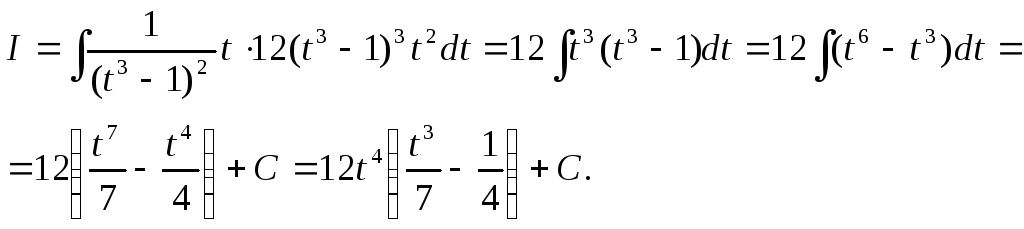
Возвращаясь к старой переменной, при помощи равенства получим

3. Найти интеграл

Найти интеграл в виде , заключаем, что. Так как– (целое число), то имеем третий случай интегрируемости.

Подстановка гдеs– знаменатель числаp, в данном случае примет вид , откуда

,,

Следовательно,

Найти интегралы:

10.133.10.134.10.135.

10.136.10.137.10.138.

10.139.10.140.10.141.

Глава 11. Определенный интеграл Краткая теория

1.Пусть функциязадана на отрезке. Разобьем отрезокнаэлементарных отрезков точками

В каждом из отрезков разбиения выберем произвольно точкуи положим, где. Тогда сумма вида

(11.1)

называется интегральной суммой для функциина отрезке.

Пусть существует и конечен предел интегральной суммы (11.1) при стремлении к нулю длины максимального элементарного отрезка, не зависящий от способа разбиения отрезкана части и способа выбора точекна отрезках разбиения. Тогда функцииназывается интегрируемой на, а число-определенным интегралом отна, и обозначается:

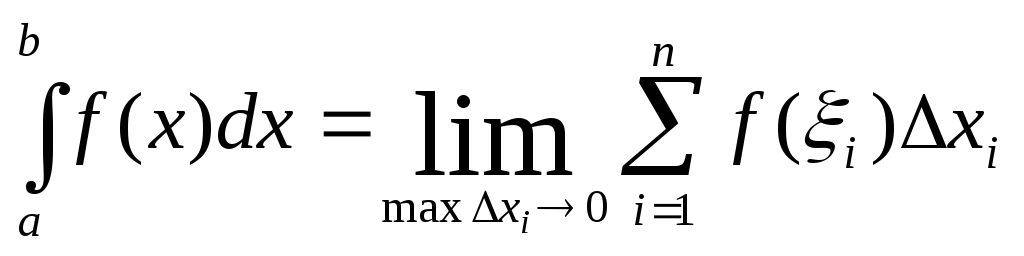(11.2)

Достаточным условиеминтегрируемости функции является ее непрерывность на рассматриваемом отрезке.