Глава 9. Дифференциал функции Краткая теория

1.Приращениедифференцируемой функцииможет быть представлено в виде:,(9.1)

где - производная функции;- приращение независимой переменной;- бесконечно малая величина.

2.Дифференциалом(первого порядка)функцииназывается главная, линейная относительночасть приращения функции, равная произведению производной на приращение независимой переменной:

(9.2)

Дифференциал независимой переменнойравен приращению этой переменной:

(9.3)

Поэтому дифференциал функции

(9.4)

3.Свойства дифференциала:

1) , где с =const. 2)

3) 4) (9.5)

5) 6)

4.Применение дифференциала в приближенных вычислениях.

При достаточно малых значениях ∆хприращение функции ∆у≈dy, т.е.

(9.6)

Чем меньше значение ∆х, тем точнее формула (9.6).

Если аргумент хвычислен с относительной погрешностью, то, функцияс относительной погрешностью, определяемой по формуле

,(9.7)

где - эластичность функции (по абсолютной величине).

5. Дифференциалы высших порядков.

Дифференциалом второго порядка(иливторым дифференциалом)d²yфункции

y=f(x) называется дифференциал от дифференциала первого порядка этой функции, т.е.

d²y=d(dy).(9.8)

Дифференциалом n-го порядка dⁿy называется дифференциал от дифференциала

(n– 1) –го порядка этой функции, т.е.dⁿy=d(d^n-1y).(9.9)

9.1.Найти дифференциал функцииy=x²+x+ 1 в точкех= 2 двумя способами:

а) выделяя линейную относительно ∆хчасть приращения функции ∆у;

б) по формуле dy=f′(x)dx.

Решение.

а) Приращение функции ∆у=f(x+ ∆x) –f(x) =f(2 + ∆x) –f(2) = ((2 + ∆x)²+ (2 + ∆x) + 1) – (2²+ 2 + 1) = 5∆x+ ∆x². Выделяя линейную относительно ∆xчасть приращения функции, получаем, чтоdy= 5∆x= 5dx.

б) Дифференциал функции dy= (x²+x+ 1)′dx= (2x+ 1)dx= (2∙2 + 1)dx= 5dx.

9.2.Найти 1,005^0,5; 1,03⁵.

Решение. Получим вначале приближенную формулу для вычисления любойn-й степени. Полагаяf(x) =xⁿ, найдемf′(x) =nx^n-1и в соответствии с (9.6):

(x+ ∆x)ⁿ≈xⁿ+nx^n-1∆x. В данном примере дляx= 1:

1,005^0,5≈ 1 + 0,5∙0,005 = 1,0025; 1,03⁵≈ 1 + 5∙0,03 = 1,15.

9.3.Использую понятие дифференциала, вычислить приближенноarcsin0,51.

Решение.Рассмотрим функциюy=arcsinx. Полагаяx= 0,5, ∆x= 0,01 и применяя формулу (9.6), имеем:

arcsin(x + ∆x) ≈ arcsin x + (arcsin x)′ ∆x = arcsin x + .

Следовательно,

arcsin0,51 ≈arcsin0,5 +

9.4.С какой точностью может быть вычислен объем шара, если его радиус измерен с точностью до 1%?

Решение.Объем шара радиусаxравенf(x) = (4/3)πx³. Найдемf′(x) = 4πx², и по формуле(9.7).

9.5.Найти количество лет, в течение которых первоначальная сумма вклада увеличится в два раза, если ставка банковского процента (за год) равнаr.

Решение. Найдем количество летT, в течение которых первоначальная сумма вклада увеличится в два раза. Так как за год вклад увеличивается в (1 +r/100) раз, то заTлет вклад увеличится в (1 +r/100)^Tраз. Таким образом, необходимо решить уравнение (1 +x/100)^T= 2. Логарифмируя, получаемTln(1 +r/100) =ln2, откудаT=.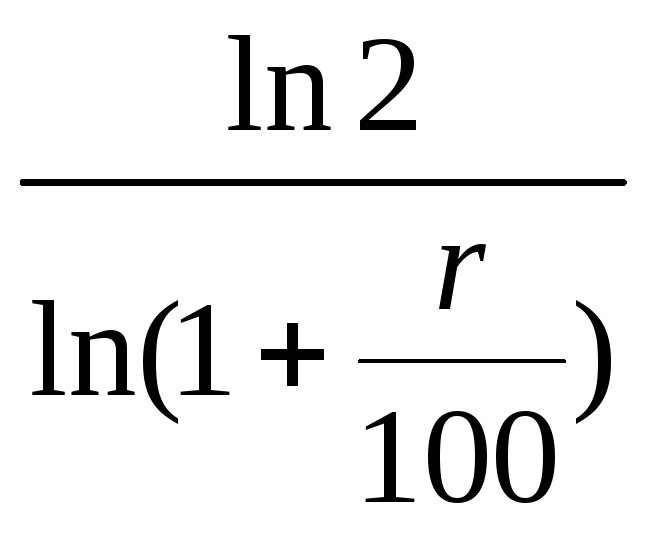

Для приближенного вычисления значения ln(1 +r/100) используем понятие дифференциала. Получим вначале приближенную формулу для вычисленииlnx. Полагая

f(x)=lnx, найдемf′(x) = 1/xи в соответствии с (9.6)ln(x+ ∆x) ≈. В данном примере дляx= 1, ∆x=r/100 получимln(1 +r/100) =ln1 +r/100 =r/100. Таким образомT≈ 100ln(2/r). Так какln2 ≈ 0,7, получаем, что время удвоения вкладаT≈ 70/r(лет).

9.6.Найтиdyиd²y, еслиy=.

Решение: ;.

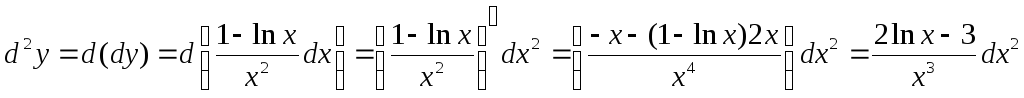Найти приращения функций и их дифференциалы и вычислить их значения при заданных xи ∆x: