11.38. 11.39..

11.40.(фигура расположена в первой четверти).

11.41. . 11.42..

11.43. . 11.44..

11.45. .

11.46. .

11.47. .

11.48. .

11.49. (фигура расположена во второй четверти).

11.50. .

11.51. и касательная к графику этой функции в точке с абсциссой .

11.52. . 11.53..

Найти длину дуг следующих кривых:

11.54. . 11.55..

11.56.

11.57. .

Найти площадь поверхности вращения, полученных при вращение вокруг оси Ох следующих кривых:

11.58. . 11.59..

11.60. . 11.61..

Найти объем тел, образованных при вращение вокруг оси Ох и Оу плоских фигур, ограниченных линиями:

11.62. .

11.63. .

11.64. .

11.65. .

11.66. .

11.67. .

11.68. .

11.69. .

11.70. .

11.71. .

11.72. Найти объем тела, полученного при вращение фигуры, ограниченной линиями вокруг прямых:а) ; б) .

11.3. Несобственные интегралы

А. Несобственные интегралы с бесконечными пределами интегрирования

Краткая теория

Пусть функция интегрируема на произвольном отрезке .

Несобственным интегралом (первого рода) называется предел функции при, т.е.

(11.22)

Если предел, стоящий в правой части равенства (11.22), существует и кончен то

соответствующий несобственный интеграл называется сходящимся; в противном случае — расходящимся.

Аналогично, по определению,

, (11.23)

, (11.24)

где а — некоторое число. При этом несобственный интеграл, стоящий

в левой части равенства (11.24), называется сходящимся, если сходятся оба несобственных интеграла из правой части этого равенства; в противном случае — расходящимся.

11.73. Вычислить интегралы:

а) ;б);в) ;

если они сходятся.

Решение. По определению (11.22), получаем

б) по определению,

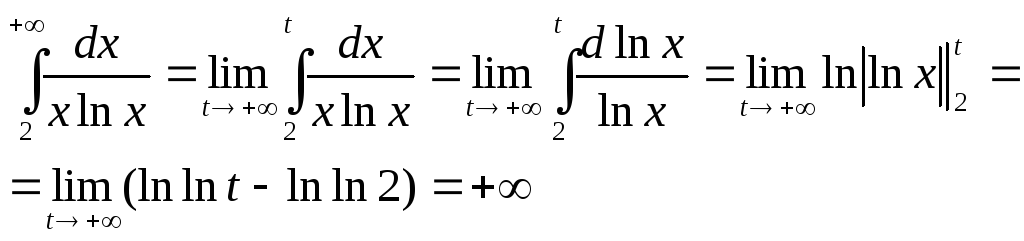
т.е. данный интеграл расходится.

в) Полагая в определении (11.24), что а = 0, учитывая четность подынтегральной функции, имеем

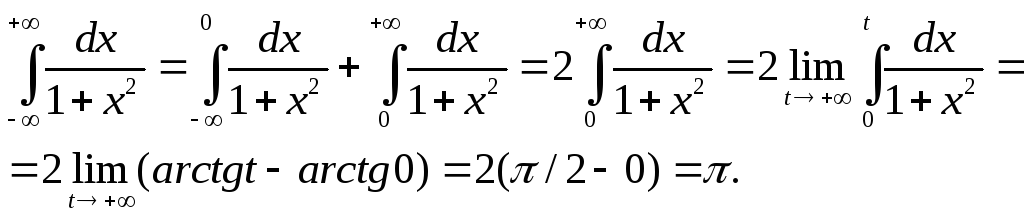
Б. Несобственные интегралы от неограниченных функций Краткая теория

Пусть функция — непрерывна, но не ограничена на полуинтервале . В этом случае интегралназываетсянесобственным (второго рода) и, по определению,

(11.25)

Если предел, стоящий в правой части последнего равенства, существует и конечен, то этот интеграл называется сходящимся; в противном случае — расходящимся.

Аналогично, если функция непрерывная, но неограниченная на полуинтервалето, по определению, (11.26)

Геометрически несобственные интегралы второго рода от неотрицательных функций численно равны площадям под графиками этих функций на рассматриваемых промежутках.

Если функция не является непрерывной в некоторой внутренней точке отрезка интегрирования,то интегралы от таких функций на данном отрезке сводятся к несобственным интегралам

(11.25), (11.26) с помощью свойства (11.7) определенного интеграла.

11.74. Вычислить интегралы:

а) ; б) ;

Решение:

а) Подынтегральная функция не ограничена вблизи точких =1. Согласно (11.25), имеем

Геометрический смысл полученного результата: площадь под кривой на полуинтервале [0,1) равна π /2 (ед.² ) (рис. 11.16).

б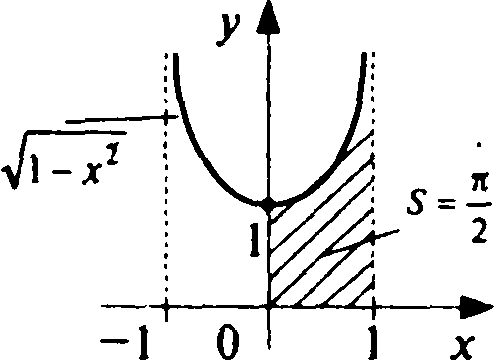) Подынтегральная функция не определена во внутренней точкех = 1 отрезка интегрирования [-7, 2] и не ограничена вблизи точки. Используя свойство (11.7) определенного интеграла, запишем исходный интеграл в виде суммы двух слагаемых:

Рис.11.16

,

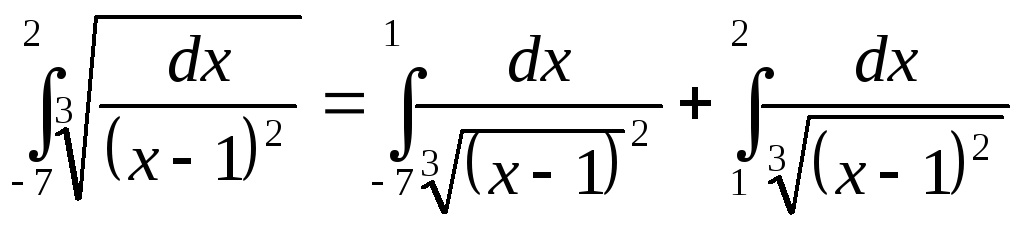для вычисления, которых применим определения (11.25), (11.26) (соответственно). Тогда получаем:

.

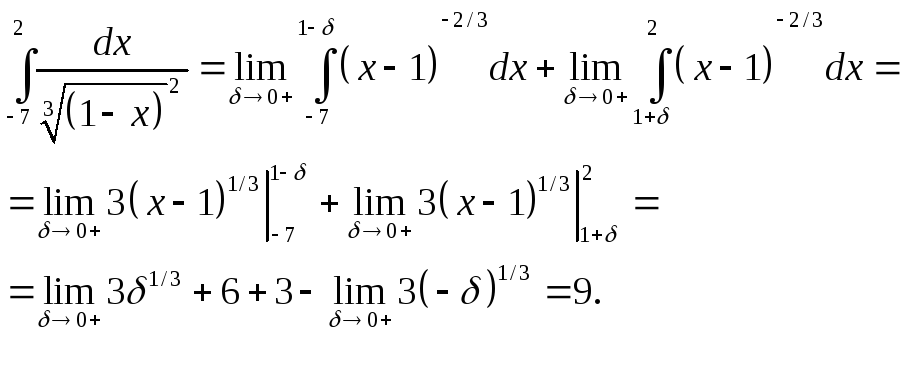Вычислить интегралы (если они сходятся):