Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кубанский государственный аграрный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ch_2_-_Pr-m_Gl_8-11

.pdf

Скачиваний:

Добавлен:

21.05.2015

Размер:

787.4 Кб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

Глава 8.

8.1. Основные теоремы дифференциального исчисления

Краткая теория

1.Теорема Ролля. Пусть функция y = ƒ(x) удовлетворяет следующим условиям:

1)непрерывна на отрезке [a,b];

2)дифференцируема на интервале (a,b);

3)на концах отрезка принимает равные значения, т.е. ƒ(a) = ƒ(b).

Тогда внутри отрезка существует по крайней мере одна такая точка ξ (a,b), в которой производная равна нулю: ƒ ′(ξ) = 0.

2. Теорема Лагранжа. Пусть функция y = ƒ(x) удовлетворяет следующим условиям:

1)непрерывна на отрезке [a,b];

2)дифференцируема на интервале (a,b).

Тогда внутри отрезка существует по крайней мере одна такая точка ξ (a,b), в которой выполняется равенство:

ƒ ′(ξ) =

ѓ(b) − ѓ(a)

(8.1)

8.1.

b − a

Выяснить,

может

ли

быть

применена

теорема

Лагранжа

для

функции

y = 3

1 − x2

на отрезке:

3 5

1 1

1 3

а)

−

;

б)

;

в)

;

2 2

Решение.

а) Функция не является непрерывной в точке x = 0 −

;

, поэтому на данном

отрезке теорема Лагранжа неприменима.

б) y′ = −

−

Производная не существует в точке x = 1

;

, поэтому

(1 − x2 )2

на этом отрезке теорема Лагранжа также не может быть применима.

3 5

в) на отрезке ; оба условия теоремы Лагранжа выполнены, так что теорема

2 2

применима.

Замечание. Если теорема Лагранжа не применима на отрезке [a,b], то это не означает, что в нем не может быть точки ξ, удовлетворяющей равенству (8.1).

8.2. Указать хотя бы одно значение a, при котором функция y = e x + a cos x имеет на

интервале (0; π ) точку, в которой производная обращается в нуль. 2

Решение. Очевидно, функция непрерывна на отрезке [0; π ] и дифференцируема в

		2
интервале (0; π ). Если при этом окажется, что ƒ(0) = ƒ(		π ), то требуемая точка будет
2		2
существовать по теореме Ролля. Таким образом, если выполняется равенство
π
2	то условие задачи будет выполнено. Рассматривая это
e0 + a cos0 = e + a cos π ,
2
		π
равенство как уравнение относительно a, получаем a = e		2 -1.

Отметим, что найденное значение a, безусловно, не единственное, при котором условие задачи выполняется.

sin πx

8.3. Найти все значения a, при которых функция y = (1+a2) 2 2 + x удовлетворяет условию y′ ≤ 2 при всех x (0;1).

Решение. Так как функция непрерывна на отрезке [0;1] и дифференцируема в интервале (0;1), то существует точка ξ (0;1) такая, что ƒ ′(ξ) = ƒ(1)-ƒ(0) =

= 2(1 + a2) + 2-(1 + a2) = 3+a2 ≥3, при любых значениях a. Таким образом, ни при каких значениях а условие задачи выполняться не может.

8.4. Функция y = 3 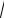x2 равна 1 при x =1 и x =-1, но y′ ≠ 0 для всех x (-1;1). Выяснить, противоречит ли это условиям теоремы Ролля?

8.5. Выяснить, применима ли для функции у = 1 + х на промежутке [-2;-1]:

а) теорема Ролля; б) теорема Лагранжа.

8.7.Дифференцируемая при всех значениях х функция у = ƒ( х) удовлетворяет условиям ƒ(2) = 5, ƒ(4) = 3. Для какого значения а уравнение ƒ ′(х) = а заведомо имеет решение?

8.8.Функция у = ƒ (х) имеет производную, равную у′ = 2 + 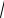1 + х2 + sin(2х + 3). Может

ли выполняться равенство ƒ(1)- ƒ(0) = sin α?

8.2. Правило Лопиталя Краткая теория

1. Теорема( правило Лопиталя).Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных ( конечному или бесконечному), если последний существует в указанном смысле:

lim

f (х)

lim

f ′(х)

(8.2)

x→ x0 (∞) g(х)

x→ x0 (∞) g ′(х)

Таким образом, правило Лопиталя используется для раскрытия неопределенностей

∞

вида

или

∞

2. Правило Лопиталя можно применять также и для раскрытия неопределенностей

вида [0·∞]. Для этого произведение f(x)g(x) следует записать в виде	f (x)	или		g (x )	и
	1	или		1	и

	g(x)

			f(x )

получить неопределенность вида	0	или	∞	.
			∞
	0

3. Если имеется неопределенность вида [00] или [∞0], при вычислении предела функции f(x)g(x), то логарифм этой функции представляет собой неопределенность вида [0·∞]. При этом используется соотношение (полученное на основе свойств логарифмов и непрерывности показательной функции):

		lim		g (x )ln f (x )
lim f (x)g (x ) = e x→ x0 ( ∞ )				.
x→ x0 (∞)
			+ x		.
8.9. Найти lim		2 + x	+ x
8.9. Найти lim
x→−1	ln(2 + x)
Решение. Так как в данном случае имеется неопределенность вида						0	, можно
							, можно
					0

применить правило Лопиталя (8.2):

(

+ x)′

2 + x

+ x

2 + x

lim

= lim

2 +

x→−1

ln(2 + x)

x→−1

(ln(2 + x))¢

x→−1

2 + x

8.10. Найти lim

4 x - 3x

x→∞

Решение. Имеет место неопределенность вида

. Применяя правило Лопиталя

4 x - 3x

4 x

ln 4 - 3x ln 3

(8.2), получаем: lim

= lim

. Как видим, неопределенность вида

x→∞

остается. Применим правило Лопиталя еще раз.

lim

4 x ln 4 - 3x ln 3

= lim

4 x ln 2 4 - 3x ln 2 3

= ¥.

x→∞

8.12.

Найти предел

lim x

x .

x→∞

Решение. Имеем неопределенность вида [∞0]. найдем

lim ln x x

x→∞

	1
= lim

x→∞		x

¥			(ln x)¢
ln x =		= lim
			(		)¢
	¥	x→∞
				x

= lim

= 0 .

x→∞

lim x x

= e0 = 1.

По формуле (8.3) lim x x

= e x →∞

x→∞

8.13. Найти предел lim[(x -

)ln ln x]

x→1

x → 1, ln x → 0 ,

ln ln x = ln(ln x) → −∞ . Таким образом,

Решение. Так как при

то

имеем неопределенность вида [0 × ¥].

Сведем ее к неопределенности вида ¥

и применим правило Лопиталя (8.2):

(

-1)2 2

(

-1) 2

2 x

lim(x -

x ) ln ln x = lim

ln x

= lim

lim

x→0

x→1

1 -

x→1

(ln x)(2 x -1)

x→1

ln x

x→1 2 x

-1

(x -

x )2

x -1

= lim

×1 = 0 .

x→1

8.14. Найти предел lim[x ln 2 x -

1 + x + x 2

x→∞

[¥ - ¥]. Преобразуем искомый предел

Решение. Имеем неопределенность вида

1 + x + x

lim[x ln 2 x - 1 + x + x 2 ]= lim x ln 2 x 1

и найдем

отдельно

предел

x→∞

x ln

lim

1 + x + x 2

, используя правило Лопиталя (8.2):

x→∞ x ln 2 x

1 + 2x

+ 2

1 + x + x 2

lim

= lim

= 0 .

x→∞

x ln 2 x

x→∞ ln 2 x + 2 ln x

x→∞

+ 1(ln 2 x + 2 ln x)

x 2

Таким образом, lim[x ln 2 x −

]= lim x ln 2

x = ∞ .

1 + x + x 2

x→∞

Найти пределы, используя правило Лопиталя:

ln 2 (1 + x)

e x

+ e− x

− 2

+ ln(1 + x)

8.15. lim

8.16. lim

8.17. lim

1 + x

x 2

x→0

8.18. lim

x 2

8.19. lim x ln3 x .

8.20. lim

e3x

− e2 x − x

x 2

x→∞ ln(e x2 + 1)

x→0

8.22. lim(x ln x −

sin x + cos x

8.21. lim x 2 (1 − e

) .

1 + x 2

) .

8.23. lim

x→∞

x→−

x + π

ln(1 + x) − ln 2

8.24. lim

arctgx

8.25. lim

8.26. lim

sin(sin

x→0

tgx

x→1

x−

x→0

1 + x − 1

+ 2x

− 3

8.27. lim(x +

x ) x .

x→∞

−

8.30.

lim

e x

x→1 x − 1

− e

8.33. lim

arcsin x

x→0

sin x

8.28.

8.31.

8.34.

x − 3 2 x −2 lim . x→2 x − 2

lim(sin x −			x	) x .
x→0
	1		+ ln(1 +
lim
lim
		+ 1)
x→−1 sin(x		+ 1)

8.29.	lim		ln ln(x 2 − 1)
							.
							.
	x→2			ln(x − 2)
				ln	x 2
8.32.	lim			ln	π	.
8.32.	lim			sin x 2		.
	x→	π		sin x 2

x) .

8.3. Интервалы монотонности и экстремумы функции

Краткая теория

1.Если производная функции y = f(x) положительна (отрицательна) во всех точках промежутка, то функция y = f(x) монотонно возрастает (убывает) на этом промежутке.

2.Точка x0 называется точкой максимума (минимума) функции y = f(x), если существует интервал, содержащий точку x0, такой, что для всех x из этого интервала имеет место неравенство f(x0) ≥ f(x), (f(x0) ≤ f(x)). Точки максимума и точки минимума называются точками экстремума.

3.Необходимое условие экстремума: в точке экстремума функции ее производная либо равна нулю (f ′(x)=0), либо не существует.

4.Первое достаточное условие экстремума: если в точке x0 функция y = f(x)

непрерывна, а производная f ′(x) при переходе через точку x0 меняет знак, то точка x0 – точка экстремума: максимума, если знак меняется с «+» на «-», и минимума, если с «–» на

«+».

Если при переходе через точку x0 производная не меняет знак, то в точке x0 экстремума нет.

5.	Второе	достаточное условие экстремума: если	в	точке x0	f	′	а
						(x0 ) = 0 ,
′′	> 0 , то x0	является точкой максимума функции. Если	f	′	′′		то
f (x0 )				(x0 ) = 0 , а	f	(x0 ) < 0 ,

x0 является точкой минимума функции.

6. Схема исследования функции y = f (x) на экстремум:

1) найти производную y′ = f ′(x) ;

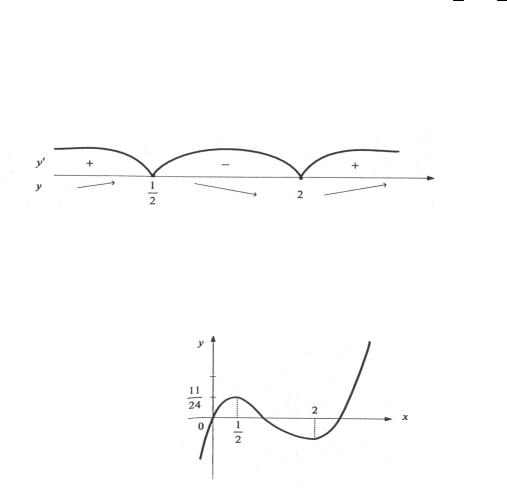
2)найти критические точки функции, в которых производная равна нулю или не существует;

3)исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции;

4)найти экстремальные значения функции.

При исследовании функции на экстремум с помощью 2-го достаточного условия п. 1), 2), 4) сохраняются, а в п. 3) необходимо найти вторую производную f ′′(x) и определить ее знак в каждой критической точке.

7. Чтобы найти наибольшее и наименьшее значение (глобальный максимум и минимум) функции y = f (x) на отрезке [a,b] следует выбрать наибольшее (наименьшее) из значений функции в критических точках, находящихся в интервале (a,b) и на концах отрезка (в точках a и b).

8.Если дифференцируемая на интервале (a,b) функция y = f (x) имеет

единственную точку экстремума, то в этой точке достигается наибольшее или наименьшее значение (глобальный максимум или минимум) функции на интервале (a,b).

8.35. Найти интервалы монотонности и экстремумы функции y = 2 x3 − 5 x 2 + 2x . 3 2

Решение. В соответствии со схемой исследования (п. 6) найдем y′ = 2x 2 − 5x + 2 . Очевидно, производная существует при всех значениях x. Приравнивая y′ к нулю,

получаем уравнение 2x 2 − 5x + 2 = 0 откуда x =	1	и x		= 2 - критические точки. Знаки
			2
1	2

производной имеют вид (рис. 8.1):

Рис. 8.1

		− ∞;	1		(2;+∞) производная f ′(x0 ) > 0
На интервалах				и		и функция возрастает, на
На интервалах				и		и функция возрастает, на
			2
1
интервале	;2 f ′(x0 ) < 0 и функция убывает;
интервале	;2 f ′(x0 ) < 0 и функция убывает;
2

Рис. 8.2

x =	1			1	=	11	, x = 2 - точка минимума и f min (2) = −	2
		- точка максимума и	f max						, так
	2					24		3
				2

как при переходе через эти точки производная меняет свой знак соответственно с «+» на

«-» и с «-» на «+».

Замечание. Установить существование экстремума в критических точках

x =

x = 2 , в которых

f ′(x0 ) = 0 можно

было

помощью второй

производной

f ′′(x) = 4x − 5 (см.

п.

5). Так как f

′′

= −3

< 0 ,

f ′′(2) = 3 > 0 , то

x =

- точка

максимума, а x = 2

- точка минимума.

График данной функции схематично показан на рисунке 8.2.

8.36. Найти экстремумы и интервалы монотонности функции y = (x ln x − x) 2 .

Решение. y′ = 2(x ln x − x) ln x + x

− 1 = 2x ln x(ln x − 1) .

Производная существует во всех точках, в которых существует и сама функция, т.е. при x > 0. Точки, в которых производная обращается в нуль, задаются равенствами ln x =0, ln x-1 = 0, откуда x1 =1, x2 = е – критические точки. Знаки производной указаны на рис. 8.3.

Рис.8.3

Таким образом, функция монотонно возрастает на промежутках (0;1) и (е;+ ∞ ) и


монотонно убывает на промежутке (1;е). Точка x =					1 – точка максимума и f max (1) = 1 ,
точка х = е – точка минимума и f min (e) = 0 .
8.37. Найти экстремумы и интервалы монотонности функции y =							.
8.37. Найти экстремумы и интервалы монотонности функции y =						1 − cos x	.
	y′ =		sin x
Решение.				. Производная не существует при cos x =1 т.е. при x = 2πn
Решение.				. Производная не существует при cos x =1 т.е. при x = 2πn
		2 1 − cos x
и равна нулю	при	x = π + 2πn . Знак производной			совпадает со знаком sin(x); таким

образом у' >0 при 2πk < x < π + 2πk и y'<0 при − π + 2πk < x < 2πk . Это, соответственно,

интервалы возрастания

убывания

функции. x = π + 2πk -

точки

максимума

f max (π + 2πk ) =

, x = 2πk

- точки минимума f min (2πk ) = 0 .

8.38. Найти наибольшее значение (глобальный максимум) функции y =

x x

на

8 − 3

интервале (10;18).

y′ =

(4 −

Решение.

Найдем

x )

. На интервале (10;18)

имеется

всего

одна

(8 − 3 x )2

критическая точка x = 6. Производная при переходе через эту точку меняет знак с «+» на «-», т.е. x = 6 – точка максимума. Следовательно, функция достигает наибольшего значения при x = 16, т.е. f наиб = f max (16) = −16 . (Заметим, что наименьшего значения (глобального минимума) данной функции на указанном интервале не существует.)

8.40. Забором длиной 24 метра требуется огородить с трех сторон прямоугольный палисадник наибольшей площади. Найти размеры палисадника.

Решение. Пусть длины сторон палисадника x,y. Тогда 2x + y = 24, т.е. y = 24-2x.

Площадь палисадника S = xy = x(24-2x) = 24x-2x2, где 0<x<12 (ибо 24-2x>0). Таким образом, задача свелась к отысканию значения x, при котором S(x) принимает наибольшее значение на интервале (0;12). Найдем S'(x) = 24-4x = 0 при x = 6. Легко видеть, что x = 6 – единственная точка экстремума – максимума функции S(x). Это означает, что на

интервале (0;12) S(x) принимает наибольшее значение при x = 6, т.е. искомые размеры палисадника 6 м и 24- 2 - 6 = 12 м.

Найти интервалы монотонности и экстремумы функции:

8.41.	y =		1	x 4 −					1	x3 − x 2 .
8.41.	y =			x 4 −						x3 − x 2 .
		4					3
8.44.	y =		x3				.

		1 + x
		1 + x
8.47.	y =		e2 x			.
8.47.	y =					.
		1 + x
	y =										.
8.50.	y =			xe3x			+ 1				.
8.53. y = ln(1 + 2 cos x) .
8.56. y =			x 2		.
8.56. y =					.
			ln x
8.59. y =			1		−			1				.
8.59. y =					−							.
			ln x					ln 2 x

8.42.

8.45.

8.48.

8.51.

8.54.

8.57.

y =	x	.

	ln x

y = x3 (x − 1)

− 4 x

y = (1 + x2 )e 5 .

y = 4 x 4 − 4x3 .

y = arctg ln x . x

y = 1 + x . 3 + x

					−	x
8.43. y = (2x + 1)e 2 .
8.46.	y =	x3
				.
		1 + x 2
		− 3x2
8.49.	y = x3e		2		.

8.52. y = x ln x − 3x .

8.55. y = 2x 2 lnx .

8.58. y = cos(lnx) .

8.60. y = 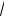1 − 2 sin x + 1 + 2 sin x .

Найти наибольшее и наименьшее значение (глобальный максимум и минимум) функции y = f (x) на отрезке [a,b]:

8.61.

f (x) = x3 − 3x;[−1;4].

8.62.

f (x) = x ln x;[0,1;1].

8.63. f (x) =

;[0;3].

2 + x 3

8.64.

f (x) = 3sin x + 4 cos3 x;[0; π ].

8.65.

f (x) =

x + 1

;[−1;1].

8.66. f (x) =

2x − 1

;[−2;0].

e x

2 + x 2

8.67. f (x) = 2 sin 2x + 3cos 2x;[0; π ].

8.68. f (x) =

;[−2;0,5].

+ x 4

Найти наибольшее или наименьшее значение (глобальный максимум или минимум)

функции y =

f (x) на интервале (a,b):

8.69. y = −3x 4

+ 6x 2 ; (−

;

8.70. y =

1 + x

; (0;2).

8.71. y =

2 + x2

;

−

;1 .

3 + x 2

1 − x 2

1 − x + x

1 − x

(− 1;1).

8.72. y = tg

x; − 1;

8.73. y =

8.74. y = arctg

;

1 + x − x

;

1 + x

8.75. Рассматриваются всевозможные прямоугольные параллелепипеды, основания которых являются квадратами, а каждая из боковых сторон имеет периметр, равный 6 см. найти среди них параллелепипед с наибольшим объемом и найти этот объем.

8.76. Определить размеры открытого бассейна с квадратным дном, при которых на облицовку стен и дна пойдет наименьшее количество материала. Объем бассейна V фиксирован.

8.77. Требуется огородить два участка: один в форме правильного треугольника, другой в форме полукруга. Длина изгороди фиксирована и равна Р. Определить размеры участков (сторону треугольника и радиус полукруга) так, чтобы сумма площадей этих участков была бы наименьшей.

8.78. В треугольнике с основанием a и высотой h вписан прямоугольник, основание которого лежит на основании треугольника, а две вершины - на боковых сторонах. Найти наибольшую площадь вписанного прямоугольника.

f"(x0) = 0 или не существует;

8.4. Интервалы выпуклости функции.

Точки перегиба

Краткая теория

Функция

y = f (x) называется выпуклой вверх (вниз) на промежутке, если для

любых двух значений x1, x2 из этого промежутка выполняется неравенство

x1 + x2

f (x1 ) + f (x2 )

x1 + x2

f (x1 ) + f (x2 )

Точки, разделяющие интервалы выпуклости, называются точками перегиба.

2. Если вторая производная

f"(x) функции y = f (x)

положительна (отрицательна)

на промежутке, то функция является выпуклой вниз (вверх) на этом промежутке.

3. Если x0 – точка перегиба функции y = f (x) и

f"(x0) существует, то f"(x0) = 0.

4. Если вторая производная f"(x) меняет знак при переходе через точку x0, то точка x0 является точкой перегиба функции y = f (x) .

5. Схема исследования функции на выпуклость и точки перегиба:

1) найти вторую производную функции f"(x);

2) найти точки, в которых вторая производная

3)исследовать знак второй производной функции слева и справа от найденных точек

исделать вывод об интервалах выпуклости и наличии точек перегиба;

4)найти значения функции в точках перегиба.

8.80. Найти точки перегиба и интервалы выпуклости функции y = 5х4-3х5.

Решение. y′ = 20х3 - 15х4, y" = 60х2 - 60х3 = 60х2(1-x) . Вторая производная обращается в нуль в тех же точках х1 = 0, х2 = 1, что и в предыдущем примере. Однако, на этот раз знаки второй производной следующие (рис. 8.5).

Рис. 8.5

Таким образом, функция выпукла вниз на всем интервале (- ∞; 1), и точка х = 0 не является точкой перегиба. Нетрудно увидеть, что это точка экстремума (максимума) функции. Точка х = 1 является точкой перегиба. На интервале (1; + ∞) функция является выпуклой вниз.

Рис. 8.6

8.81. Найти точки перегиба у = sin х + 2соs х.

Решение. Имеем у' = соs х-2sin x, y" = -sin x – 2cos x. Вторая производная обращается в нуль при выполнении равенства sin x = - 2 cos x, или tg x = - 2,т.е. в точках

x = - arctg 2 + πn. Рис 8.6 показывает, что при – arctg 2 + 2 πn < x < π – arctg 2 + 2 πn ƒ"( х)<0 и функция является выпуклой вниз, а при π – arctg 2 + 2 πn < x < 2π - arctg 2 + 2πn ƒ"( х) >0 и функция является выпуклой вверх. Точки х = - arctg 2 + πn – точки перегиба.

Найти точки перегиба и интервалы выпуклости функции:

8.82. y =	1	x3 (x2 - 5).	8.83. y =	x	.
8.82. y =		x3 (x2 - 5).	8.83. y =		.
6				(x2 + 1)

8.85. y = 3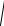1 − х3 .

8.88.y = ln x .

x 2

8.91. y = . x 2 + 1

8.86. y = (x + 1)arctg x.


8.89. y = x2e x .
x3				5x3		3x	2
8.92. y =		− x 2	ln x −		+			.
8.92. y =		− x 2	ln x −		+			.
	6			36		2
	6			36		2

8.84. y = 3 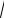x2 − 2х.

− х2

8.87. y = x3 e 2 .

8.90.y = x3lnx + 1.

8.93.y = .

33 x3 + 2

8.5. Асимптоты. Исследование функций и построение их графиков

Краткая теория

1. Прямая l называется асимптотой графика функции у = ƒ( х), если расстояние от точки (х, ƒ( х)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

Асимптоты бывают вертикальными, горизонтальными и наклонными.

2. Прямая х = xо является вертикальной асимптотой графика

функции у= ƒ( х), если хотя бы один из пределов lim	ƒ( х) (правосторонний или
x→x0 ±0

левосторонний) равен ±∞ .

Прямая х = xо может быть вертикальной асимптотой функции y = ƒ( х) в том случае, если xо – точка разрыва или граничная точка области определения.

3. Прямая у = b является горизонтальной асимптотой, если lim ƒ( х) = b. x → ∞

Если lim ƒ( х) = b, то у = b — правосторонняя горизонтальная асимптота, x → +∞

если lim ƒ( х) = b, то у = b — левосторонняя горизонтальная асимптота. x → −∞

4. Если lim	f (х)	=k	¹ 0 и lim f (х) − kх	] = b, то прямая y = kx + b является

x→∞ x			x→∞

наклонной асимптотой графика функции y = ƒ( х).

5. Общая схема исследования функций и построения графиков:

1)найти область определения функции;

2)исследовать функцию на четность – нечетность;

3)найти вертикальные асимптоты;

4)исследовать поведение функции в бесконечности; найти горизонтальные и наклонные асимптоты;

5)найти экстремумы и интервалы монотонности функции;

6)найти интервалы выпуклости функции и точки перегиба;

7)найти точки пересечения графика функции с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.

Исследование функции проводится одновременно с построением графиков.

8.94. Исследовать функцию y =	2x	и построить ее график.
	− x 2
1

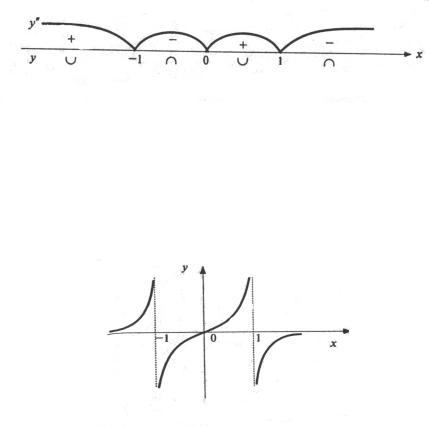
Решение:

1. Область определения (−∞;1) (−1;1) (1; +∞) . Точки x = −1 и x = 1 – точки

разрыва функции.

2. ƒ(- х) = -ƒ( х), т.е. функция нечетная; её график симметричен относительно начала координат и достаточно провести исследования функции на интервале [0;+∞).

lim

= +∞ ; lim

= −∞ .

x→1−0 1 − x 2

x→1+0 1 − x 2

Прямые х = 1 и (в силу симметрии графика) x = −1 –

вертикальные асимптоты.

lim

= 0 . Прямая у

= 0

(ось абсцисс) –

двухсторонняя горизонтальная

x→±∞ 1 − x 2

асимптота.

2 + 2x 2

y'=

> 0 при всех допустимых значениях х. Экстремумов нет, функция

(1 − x 2 )2

возрастает на интервалах (− ∞;1), (− 1;1),

(1; ∞).

6. y ''=

4x(x 2

+ 3)

, y" = 0 при х = 0.

Знаки второй производной показаны на рис. 8.7.

(1 − x 2 )3

	Рис. 8.7
Функция выпукла вниз на интервалах (− ∞;1) и (0;1)		и выпукла вверх на интервалах
(−1;0), (1;+∞).	Хотя ƒ"( х) меняет свой знак при	переходе через три точки
x = −1, x = 0 ,	x = 1, но график функции имеет только одну точку перегиба х = 1, ибо в
двух других точках x = −1, x = 1 функция не определена.
7. Точка пересечения графика с осями единственная –		начало координат (0;0).
График функции показан на рис. 8.8.

Рис. 8.8

8.95. Исследовать функцию y = (x - 1)ex и построить ее график.

Решение:

1.Область определения (− ∞;+∞).

2.	Функция общего вида, так как ƒ (-	х) = (-х - 1) L− x	¹ ± ƒ ( х).
3.	Так как функция определена	и непрерывна	на всей числовой оси, то

вертикальных асимптот нет.

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.05.2015665.6 Кб31A_Few_Glimpses_of_Ecology_metodichka.doc
#
21.05.20152.51 Mб88bibliofond.ru_732812.rtf
#
21.05.2015315.39 Кб25Bilety_po_filosofii.doc
#
02.12.2018205.31 Кб8biology.doc
#
21.05.2015357.59 Кб60Ch_1-_Pr-m_Gl_1-7.pdf
#
21.05.2015787.4 Кб46Ch_2_-_Pr-m_Gl_8-11.pdf
#
21.05.20152.94 Mб151Ch_2_-_Pr-m_Gl_8-11_-_kopia.doc
#
21.05.2015403.46 Кб16datyIstoria_Rossii.doc
#
21.05.2015720.45 Кб16Don_Failla_System.pdf
#
21.05.201537.89 Кб12Ekzamenatsionnye_voprosy_po_istorii.doc
#
21.05.2015182.52 Кб65EKZAMEN_bu.docx