Ch_1-_Pr-m_Gl_1-7

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кубанский государственный аграрный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

x 2 - 4 ³ 0,

(x - 2)(x + 2) ³ 0,

(x - 6) ¹ 0,

x +10 > 0,

.pdf

Скачиваний:

Добавлен:

21.05.2015

Размер:

357.59 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Раздел II. Введение в анализ

Глава 5.

Функция

Краткая теория

Если каждому элементу (значению) x множества

X поставить в соответствие

определенный элемент (значение) y множества Y , то говорят, что на множестве

задана функция y =

f (x) ; при этом множество X

называется областью определения

функции y , а множество Y - областью значений функции y .

Функция

y = f (x) называется четной, если для любых значений

из области

определения функции

f (- x) = (x) , и нечетной, если

f (- x) = - f (x). В противном случае

f (x) - функция общего вида.

Функция

y = f (x)

называется

возрастающей

(убывающей)

на

некотором

промежутке X , если большему значению аргумента соответствует большее (меньшее)

значение функции

f (x) .

Возрастающие

или

убывающие функции

называются

монотонными.

f (x)

4. Функция

называется ограниченной на промежутке X , если существует такое

число M > 0 , что

f (x)

< M , для всех

x X .

В противном случае функция называется

неограниченной.

5. Если функция y = f (u) есть функция переменной u

(определенной на множестве

U с областью значений Y ),

а переменная u ,

в свою очередь, также является

функцией

u = ϕ(x)

(определенной на

множестве

областью значений U ), то заданная на

множестве X функция y = f [ϕ(x)] называется сложной функцией.

6. Основные элементарные функции:

а) степенная функция y = x n ;

б) показательная функция y = a x , a > 0, a ¹ 1

(X = (-¥;+¥);Y = (0;+¥)) ;

в) логарифмическая функция y = log a

x, a > 0, a ¹ 1

(X = (0;+¥); Y = (- ¥;+¥));

г) тригонометрические функции y = sin x, y = cos x, y = tgx, y = ctgx ; д) обратные тригонометрические функции

y= arcsin x, y = arccos x, y = arctgx, y = arcctgx .

7.Функции, построенные из основных элементарных функций при помощи конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.

Функция

y = f (x) называется

периодической

с периодом

T ¹ 0 , если

f (x + T ) = f (x) для любых x Î X .

Преобразование графиков:

а)

y = f (x + a) - сдвигает график y = f (x) параллельно оси Ox на

единиц, ( a > 0

- влево, a < 0 - вправо);

б)

y = f (x) + b

- сдвигает график y = f (x) параллельно

оси Oy на

единиц ( b > 0

- вверх, b < 0 - вниз);

в)

y = cf (x)(c ¹ 0) - растягивает в

c раз (c > 1) или

сжимает (0 < c < 1) график

y = f (x) относительно оси Oy ; при c < 0

симметрично отображает график относительно

оси Ox ;

г) y = f (kx)(k ¹ 0) - растягивает в k раз (k > 1)	или сжимает (0 < k < 1) график
y = f (x) относительно оси Ox , при k < 0 симметрично	отображает график относительно
оси Oy .

10.Абсолютная величина (модуль) действительного числа x :x, если x ³ 0;

=- <

x, если x 0.x

5.1.Найти область определения функции

y = х(2 - 4) + ln(x +10) . 2 x x - 6

Решение. Так как выражение под корнем четной степени должно быть неотрицательно, знаменатель дроби отличен от нуля, а выражение, стоящее под знаком логарифма, должно быть положительно, то область определения функции найдем из системы неравенств:

x Î (- ¥;-2]È[2;+¥),¹

x 6,

x Î (-10;+¥).

Значения переменной x , которые удовлетворяют всем неравенствам системы одновременно, есть x Î (-10;-2] È [2;6)È (6;+¥) .

5.2. Найти область значений функции y = 10−2 x2 .

Решение. Воспользуемся определением обратной функции, в соответствии с которым область ее определения будет являться областью значений исходной функции.

Найдем функцию, обратную к функции y = 10−2 x 2 , выражая x через y : -2x 2 = lg y или

x 2 = - 1 lg y .

Так как

x 2 ³ 0 , то -

lg y ³ 0 ,

откуда

lg y £ 0 и

y Î (0;1], т.е.

найденный

полуинтервал и является областью значения искомой функции.

5.3. Выяснить четность (нечетность) функции:

а) y =

- 1 - x2 ; б)

y = 3x sin x .

cos x

Решение:

(- x)4

а) Найдем y(- x) =

x 4

1 - (- x)2

- 1 - x 2

cos(- x)

cos x

Так как y(- x) = y(x), то по определению (п.2) искомая функция является четной;

б) y(- x) = 3− x sin(- x) = 3− x - sin x

так как

y(- x) ¹ y(x)

и y(- x) ¹ -y(x), то по

определению (п. 2) искомая функция является функцией общего вида.

5.4. Найти основной (наименьший) период функции y = 2 sin 4x .

Решение: По определению периодической функции (п. 8) y(x + T ) = y(x) для любых

x и T ¹ 0 . Для f (x) = 2 sin 4x имеем:

2 sin(4(x + T )) = 2 sin 4x ,

или

sin(4x + 4T ) - sin 4x = 0 ,

откуда

2 sin 4x + 4T − 4x × cos 4x + 4T + 4x = 0 . т.е. sin 2T × cos(4x + 2T ) = 0 . Полученное равенство

2	2
будет выполняться при любых x ,		т.е. тождественно, если сомножитель, не содержащий
x , будет равен нулю, т.е. sin 2T = 0		и наименьшее (не равное нулю) T = π / 2 .

5.5. Постоянные издержки F (не зависящие от числа х произведенной продукции) составляют 125 тыс. руб. в месяц, а переменные издержки V (x) (пропорциональные x ) – 700 руб. за каждую единицу продукции. Цена единицы продукции 1200 руб. Найти объем продукции x , при котором прибыль равна: а) нулю (точка безубыточности); б) 105 тыс.

руб. в месяц.

Решение:

а)

Издержки

производства

единиц

продукции

составят:

C(x) = F +V (x) = 125 + 0,7x (тыс. руб.). Совокупный доход (выручка)

от реализации этой

продукции R(x) = 1,2x ,

а прибыль P(x) = R(x) - C(x) = 0,5x -125

(тыс. руб.). Точка

безубыточности, в которой P(x) = 0,5x -125 = 0 , равна x = 250 (ед.).

б) прибыль P(x) равна 105 (тыс. руб.), т.е. P(x) = 0,5x -125 = 105 при x = 460 (ед.).

5.6. Продолжительность выполнения

y (мин.) при повторных операциях связана с

числом x этих операций зависимостью y =

. Вычислить, сколько минут выполняется

x + c

работа при 50 операциях, если известно, что при x = 20 y = 125 , а при x = 200

y = 50 .

Решение. Найдем параметры a и c , учитывая, что y(20) = 125 ,

y(200) = 50 . Имеем

систему:

125

+ c

50 =

200

+ c

решая которую найдем a = 15000, c = 100 .

Итак, y = 15000 и при x = 50 y(50) = x +100

Найти области определения функций:

5.12.y = 5 lg(x +1) + 210− x .

x-1

=6 16 - x 2

5.13.y lg(x -1)2 .

5.14.y = 4 - x 2 × tgx .

Найти области значений функций:

5.17.y = 5sin x + 2 cos x .

−x 2

5.18.y = e 2 .

5.19. y =	3x	.
	+ x 2
1

Выяснить четность (нечетность) функций:

5.22.y = x + sin x .

5.23.y = x × sin 3 x .

5.24.y = lg(1 - x 2 )× e− x2 .

3 cos x

15000

50 +100

= 100 (мин.).
5.15. y = arcsin(x − 1) .
lg x
5.16. y = sin x - 0,5 - log	2 (x -1).
3 x - 2

5.20.	y =	3	.
		(sin x + cos x)2 + 2
5.21.	y = logπ (arccos x).

5.25. y =	x3	cos x			+ sin 2 x .
5.25. y =		2 x	2		+ sin 2 x .
		2 x
		2 - x		3
		2 - x
				3
5.26. y = lg		2 + x		3		.
		2 + x

Найти наименьший период функций или доказать их непериодичность:

5.31.y = x sin x .

5.32.Дана функция y(x) =

5.33.Дана функция y = 2 x

5.34.Известно, что y(x) =

5.35.Известно, что y(x) =

1 + x

4 − x

, найти

1 − x

2 + x

,найти y(log0.5 x).

3 − x

1 + z(x)

. Найти z(x).

, а

2 + x

3x , а y(4z(x)) =

. Найти z(x).

x 2

5.38.Предприятие купило автомобиль стоимостью 150 тыс. руб. Ежегодная норма амортизации составляет 9 %. Полагая зависимость стоимости автомобиля от времени линейной, найти стоимость автомобиля через 4,5 года.

5.39.Зависимость уровня потребления у некоторого вида товаров от уровня дохода

	y = a −	b
семьи х выражается формулой:				. Найти уровень потребления товаров при
		x
			+ c
уровне дохода семьи 158 ден. ед. Известно, что при x = 50 y = 0 ; при x = 74					y = 0,8 ; при
x = 326 y = 2,3 .
5.40. Банк выплачивает ежегодно 5%			годовых (сложный процент). Определить: а)
размер вклада через 3 года, если первоначальный вклад составил 10 тыс. руб.;
б) размер первоначального вклада, при котором через 4 года вклад (вместе с
процентными деньгами) составит 10000 руб.
						p t
Указание. Размер вклада Qt	через t лет определяется по формуле Qt =				Q0 1 +		,

						100
где p - процентная ставка за год,	Q0 - первоначальный вклад.

Глава 6. Пределы и непрерывность Краткая теория

1. Если по некоторому закону каждому натуральному числу п поставлено в соответствие определенное число ап, то говорят, что задана числовая последовательность

{ап}.

2. Число А называется пределом числовой последовательности {ап}, если для любого e > 0 найдется такой номер N, зависящий от e, что для всех членов последовательности с

номерами п > N верно неравенство	an	- A	< e (lim an = A).

			n→∞

3. Число А называется пределом функции у = f(х) при х ® ¥, если для любого

e > 0 найдется также число S > 0, зависящее от e, что для всех х таких, что |х| > S

будет верно неравенство	f ( x ) - A	< e (lim	f ( x ) = A ). .
будет верно неравенство	f ( x ) - A	< e (lim	f ( x ) = A ). .
		x → ∞
		x → ∞
4. Число А называется пределом функции f(х) при х ® x0 , если для любого e > 0
найдется число d > 0, зависящее от e, что для все х ≠ x0 и удовлетворяющих условию
\|x – x 0\| < d выполняется неравенство			f ( x ) - A

				< e lim	f ( x ) = A .
				x → x 0
				x → x 0

5. Функция a(х) называется бесконечно малой величиной при х ® x0 (или
х ® ¥), если
х ® ¥), если	lim a ( x ) = 0 lim		a ( x ) = 0 .
	x → x 0	x → x 0

6. Функция f(x) называется бесконечно большой величиной при х ® x0 , если для любого М > 0 найдется такое число d > 0, зависящее от М, что для всех х ≠ x0 и

7. Свойства бесконечно малых. Если a(х) и b(х) —

бесконечно малые величины при

х ® x0

(или х ® ¥),

то будут бесконечно малыми величины: a(х) ± b(х); с × a(х),

с –

постоянная;

f(x)×

a(х)

(f(x)

–

ограниченная

функция);

a(х) ×

b(х);

a ( x )

lim

( x )

0 .

f ( x )

x → x 0 ( ∞ )

8. Свойства бесконечно больших. Если f(x) и j(х) – бесконечно большие величины

при

х ® x0

(или

¥),

то

будут

бесконечно

большими

величинами:

f(x) + j(х) (j(х)

—

ограниченная функция);

f(x)/j(х)

(j(х)

f ( x) ×j ( x) lim ( x ) ¹

0 ;

→ x0

имеет предел).

9. Если функция a(х) есть бесконечно малая величина при х ® x0 (или х ® ¥), то

функция

f (х) =

является бесконечно

большой,

и обратно, если

f(x)

бесконечно

a(х)

большая функция

при

х ® x0

(х

® ¥)

то

a(х) =

является

бесконечно

малой

f (х)

величиной.

10. Сравнение порядков бесконечно малых. Если a(х) и b(х) —

бесконечно малые

величины при х ® x0 (х ® ¥) и

lim

( x )

, то при k = 0 бесконечно

( x )

x → x 0 ( ∞ )

малая a(х) называется бесконечно малой более высокого порядка малости, чем b(х); при 0 < k < ¥ — одного порядка малости; при k = ¥ — более низкого порядка малости, чем b(х).

Если k = 1, то бесконечно малые a(х) и b(х) называются эквивалентными: a(х) ~b(х).

11.Примеры эквивалентных бесконечно малых величин при х ® 0: sin x ~ x; ln(1+x) ~ x; (1 + x) m ~ 1+ mx; arcsin x ~ x; arctg x ~ x; 1 – cos x ~ x2/2.

12.Предел отношения двух бесконечно малых величин не изменится, если эти бесконечно малые заменить им эквивалентными.

13.Теоремы о пределах:

1)	lim		C = C (C - постоянная) .
	x→ x0 (∞ )		lim f (x) = A,		ϕ(x) = B,
2) Если			lim f (x) = A,	lim	ϕ(x) = B,
		x→x0 (∞)		x→x0 (∞)
то:	lim		( f (x) +ϕ (x)) = A ± B;		lim	( f (x) ×ϕ(x)) = A × B; lim	f (x)	=	A	(B ¹ 0).
то:	lim		( f (x) +ϕ (x)) = A ± B;		lim	( f (x) ×ϕ(x)) = A × B; lim		=		(B ¹ 0).
	x→ x0 (∞)				x→ x0 (∞)	x→x0	ϕ (x) B
14. Если lim f (u) = A ,				lim ϕ (x) = uo , то lim f (ϕ (x)) = A .
			u→u0	x→ x0		x→ x0

15.Первый замечательный предел: lim sinα = 1

α→0 α

6.1. Определение предела. Простейшие пределы

Для того чтобы найти предел элементарной функции, когда аргумент стремится к значению, принадлежащему области определения этой функции, нужно в выражение функции вместо аргумента подставить его предельное значение.

6.4. Найти	lim	x2	+ 7	.
			2
	x→3

Решение. Подставляем вместо х в выражение под знаком предела 3, получим

			lim	x 2	+ 7	= lim	32	+ 7	= lim 8 = 8 .
					2			2
			x→3			x→3			x→3
6.5. Найти	lim	4	.

	x→∞ x3

Решение. Знаменатель дроби х3 при х ® ¥ является бесконечно большой величиной,

1при х ® ¥ является бесконечно малой величиной, следовательно, искомый предел

равен нулю.

6.6. Найти		2x2
	lim		.

	x→4 x - 4
Решение.	Знаменатель дроби (х — 4) при х ® 4 является бесконечно малой
величиной, тогда 1/(х –		4) – бесконечно большая величина; числитель дроби 2х2 является
функцией, предел которой отличен от нуля (lim 2x2 = 32).
Функция 2х2/(х –			x→4
		4) является бесконечно большой величиной, т.е. искомый предел
равен ¥.

6.2. Раскрытие неопределенностей различных типов

Далеко не всякая подстановка предельного значения в функцию вместо независимой переменной может сразу привести к нахождению предела. Случаи, в которых подстановка предельного значения в функцию не дает значения предела, называют неопределенностями; к ним относятся неопределенности видов

¥			0			×¥], [¥ - ¥], [1∞ ], [¥0	], [00	].
	¥	,			, [0
				0

Устранить неопределенность удается часто с помощью алгебраических преобразований.

6.12. Найти

lim(x4

− 2x2 −10x).

x→∞

Решение. Имеем неопределенность вида [∞ – ∞]. Вынесем за скобку х в наибольшей

−

степени:

lim x

x→∞

х4 является бесконечно большой величиной при х → ∞. По теоремам о пределах

lim 1−

−

= lim1

− lim

= 1− 0 − 0 = 1,

x→∞

x→∞ x2

x→∞ x3

так как

при х → ∞ являются бесконечно малыми величинами, а предел

x 2

постоянной (единице).

постоянной

равен

самой

По

свойству бесконечно больших

x4 (1−

−

) является бесконечно большой величиной, т.е. искомый предел равен ∞.

Ответ данной задачи и приведенные в решении выкладки будем использовать при решении следующих примеров как заранее известные факты. Рассмотрим несколько типов примеров, классифицируя их по виду неопределенности и предельному значению х.

1-й тип. Рассмотрим примеры вида lim	f (x)	с неопределенностью вида	∞	, где

x→∞	ϕ (x)		∞

f(x) и ϕ(х) в общем случае – сложные степенные или показательные функции. В случае степенных функций необходимо выносить за скобку в числителе и знаменателе дроби х с наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется.

6.13. Найти

lim

7x − 2x4

+ 3x2 +1

x→∞ 4x4

Решение.

A = lim

7x − 2x4

∞

. Вынося за скобку и в числителе и в знаменателе

x→∞ 4x

∞

х в наибольшей степени, получим

4 7

−

− 2

0 − 2

A = lim

= lim

= −

4 + 0 + 0

x→∞

4 +

так как

, –

величины бесконечно малые при х → ∞.

x 2

x 4

3x + 2 x

6.17. Найти

lim

−

x→+∞ 1

Решение.

При x → +∞ показательная функция y = a x , при a > 1 стремится к + ∞ .

Быстрее будет возрастать та функция, у которой основание больше, поэтому в нашем

случае выносим за скобки 3x :

2 x

1 +

1 + 0

lim

= lim

= −1,

0 − 1

x→+∞

x→+∞ 1

− 1

так как при a =

< 1

lim

= 0 и при a =

< 1

lim

= 0 .

x→+∞

Найти пределы:

7x 4 + 2x3 -1

6.18. lim

6.23. lim

4 x8 + 2x -10 - 3x 2

3x 2 -

2x 4 + x

x→∞

-1 -

27x

+ x

-15x

3x3 - x 2

+ 2x

6.19. lim

6.24.

x3 - x 4

x→∞

lim

(2x +1)

+ (2x + 2)

+ (2x + 3)

+ ... + (2x +100)

- x

-15

6.20. lim

x→∞

10x5 +100

x 2

-16

x→∞

6.25. lim

3x + 2

4x 2

+ 2x -

6.21. lim

x + 3

x→∞

3 64x3 +1 + 2

x→∞ 3x+1 -1

4 x

+ 3x+1

- 9 - 2x

6.26. lim

6.22. lim

x→∞ 4 x+1 + 3x

x→∞

2 - 3

x3 + 5

2-й тип. Рассмотрим примеры вида lim

f (x)

с неопределенностью вида

. В

x→ x0

ϕ (x)

этом случае необходимо разложить на множители и числитель, и знаменатель дроби или домножить и числитель, и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.

6.45. Найти	lim	x 2 - 9		.
6.45. Найти	lim			.
	x→−3 x 2 + 7x +12
Решение. Имеем неопределенность вида					0	. Разложим числитель и знаменатель
Решение. Имеем неопределенность вида						. Разложим числитель и знаменатель
					0
дроби на множители: числитель –			по формуле сокращенного умножения

a 2 - b 2 = (a - b)(a + b), а знаменатель – по формуле разложения квадратного трехчлена на множители при = b 2 - 4ac ³ 0 :

x1,2 =

= lim

x→−3

- b ± 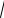b2 - 4ac . 2a

(x - 3)(x + 3) = lim x - 3 . (x + 3)(x + 4) x→−3 x + 4

После сокращения дроби следует подставить предельное значение х в сокращенную

дробь. Получим A = lim		− 3 − 3				= − 6 = -6.
		- 3 + 4
	x→−3					1
				- 8	.
6.46. Найти	lim		x

	x→64 3 x - 4

Решение. 1-й способ. Имеем неопределенность вида . Дополним числитель до

разности квадратов a 2 - b 2

= (a - b)(a + b),

а знаменатель до разности кубов

a3 - b3 = (a - b)(a 2

+ ab + b 2 ). Получим

- 8

(

- 8)(

+ 8)(3

x 2

+ 43

+16)

(x - 64)(3

x 2

+ 43

+16)

lim

= lim

x→64 3 x

- 4

x→64 (3

- 4)(

+ 8)(3

x 2

+ 43

+16)

x→64

(x - 64)(

x + 8)

+ 43

+16)

(3 642

+ 43

+16)

16 +16 +16

= lim

= 3.

8 + 8

x→64

x + 8

x→64

64 + 8

2-й способ. Сделаем замену переменной: 6 x = t, тогда 3 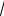x = t 2 , а 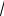x = t 3 , при

x ® 64, t ® 6 64, т.е. t → 2. Теперь

lim

- 8

= lim

t 3 - 8

x→64 3 x - 4

t →2 t 2 - 4

Найти пределы:

6.47.

x 2 - 3x + 2

lim

x 2

x→1

+ x - 2

6.48.

x 2

- x - 6

lim

x→−2 x 2

6x + 8

6.49.

x 2 - 2x

lim

x→2

x 2 - 4x + 4

6.50.

x 2 - 5x + 4

lim

x→4

2 -16

6.51. lim

x 2 -1

x→1

6.52.

lim

+ 27

x 2

- 9

x→−3

6.53. lim

x 2

- 49

x→7

= lim (t - 2)(t 2 + 2t + 4) t→2 (t - 2)(t + 2)

= lim

t 2

+ 2t + 4

= lim

+ 2 × 2 + 4

= 3.

2 + 2

t→2

t + 2

t →2

(

6.54. lim

x - 2

x 2

- 4

x→2

6.55.

x3 - 2x 2 - 5x + 6

lim

x3 - 7x +

x→1

-1

6.56. lim

x -1

x→2

x - 2

6.57. lim

x 2 -1

x→−1 3

x +1

6.58. lim

3x - 2

x→1

x -

3-й тип. Рассмотрим примеры с неопределенностью вида [∞ – ∞]. Если функция, стоящая под знаком предела, представляет собой алгебраическую сумму дробей, то неопределенность устраняется или приводится ко 2-му типу после приведения дробей к общему знаменателю. Если упомянутая функция представляет собой алгебраическую сумму иррациональных выражений, то неопределенность или устраняется, или приводится к 1-му типу путем домножения и деления функции на одно и то же (сопряженное) выражение, приводящее к формулам сокращенного умножения.

2x + 8

6.68. Найти

lim

x3 -

x→2

x -

Решение. Имеем неопределенность вида [∞ –

∞]. Приведем дроби к общему

знаменателю:

2x + 8

x 2

+ 2x + 4 - 2x - 8

x 2 - 4

A = lim

= lim

- 2)(x

+ 2x +

2)(x

+ 2x + 4)

x→2

x - 2

- 8

→2 (x

x→2 (x -

Имеем предел 2-го типа, необходимо разложить на множители числитель дроби.

Получим

(x − 2)(x + 2)

x + 2

2 + 2

A = lim

= lim

+ 2x + 4)

+ 2x + 4

x→2 (x - 2)(x 2

x→2 x 2

x→2 22 + 2 × 2 + 4

6.69. Найти lim ( x 2 - 2x - 5 - x).

x→+∞

Решение. Имеем неопределенность вида [∞ – ∞]. Домножим и разделим функцию, стоящую под знаком предела на сопряженное выражение, приводящее к разности квадратов:

(

− x)= lim

(

− x)(

+ x) = lim

− 2x − 5 − x2

A = lim

x 2 − 2x − 5

x 2

− 2x − 5

x→+∞

x 2

− 2x − 5 + x

x→+∞

x 2 − 2x − 5 + x

= lim

− 2x − 5

∞ .

x→+∞

− 2x − 5 + x

∞

Имеем предел 1-го типа.

A = lim

− 2x − 5

lim

− 2x − 5

x→+∞

1 −

−

+ x

1 −

−

+ x

x 2

При x → +∞

= x по определению модуля; поэтому

− 2x − 5

x − 2

−

− 2 −

− 2 − 0

A = lim

= lim

= −1.

x 1 − 2 − 5

+ x

1 − 2

− 5 + 1

1 − 0 − 0 + 1

1 − 2 − 5

+ 1

x→+∞

так как при x → +∞

- бесконечно малые величины.

x 2

Найти пределы:

				1				−		1
6.70.	lim															.
6.70.	lim															.
	x→−1 x +						1				x 2 − 1
						1					−				1
6.71.	lim																	.
6.71.	lim												x 2					.
	x→0 2x 2 − x												x 2		− x
				1				−		12
6.72.	lim															.
6.72.	lim															.
	x→2 x −						2				x3 − 8
				1				−		6
6.73.	lim															.
6.73.	lim															.
	x→3 x −						3			x 2 − 9
				1					−					3
6.74.	lim																.
6.74.	lim											x3					.
	x→1 x 2 − x											x3		− 1
				2x3
6.75. lim											− x .
6.75. lim					2						− x .
		2x			2		− x
	x→∞	2x					− x
			3x				4		− 3x 2
6.76. lim															.
6.76. lim				2											.
				2		+ 3
	x→∞ x					+ 3
			3x				3
6.77. lim									− 7x .
6.77. lim									− 7x .
		5x − 1
	x→∞	5x − 1

4x4

− 4x

6.78. lim

2 .

+ x + 2

x→∞ x

−

3x3

6.79. lim x

x→∞

+ 7

x 4

−

x 4

6.80. lim

− 2

+ 2

x→∞ x

6.81. lim (

−

x − 3

x + 2

x→+∞

6.82. lim (

−

x 2

+ x

x 2

− x

x→+∞

6.83. lim (

−

x 2

+ x

x 2

− 5x

x→−∞

6.84. lim (

−

2x + 10

x + 20

x→+∞

6.85. lim (

−

2x 2 − 1

x 2

+ 5

x→+∞

6.86. lim(

−

9x 2

+ 2x

9x 2 − x

x→∞

6.87. lim (3

− 3

x + 3

x→+∞

6.3.Замечательные пределы

Кпределам 4-го типа отнесем примеры с неопределенностью вида [1∞ ]. В этом

случае выражение, стоящее под знаком предела, представляет собой степеннопоказательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи выделения «второго замечательного предела» .

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.11.2018166.6 Кб7attachment.docx
#
21.05.2015665.6 Кб31A_Few_Glimpses_of_Ecology_metodichka.doc
#
21.05.20152.51 Mб88bibliofond.ru_732812.rtf
#
21.05.2015315.39 Кб25Bilety_po_filosofii.doc
#
02.12.2018205.31 Кб8biology.doc
#
21.05.2015357.59 Кб60Ch_1-_Pr-m_Gl_1-7.pdf
#
21.05.2015787.4 Кб46Ch_2_-_Pr-m_Gl_8-11.pdf
#
21.05.20152.94 Mб151Ch_2_-_Pr-m_Gl_8-11_-_kopia.doc
#
21.05.2015403.46 Кб16datyIstoria_Rossii.doc
#
21.05.2015720.45 Кб16Don_Failla_System.pdf
#
21.05.201537.89 Кб12Ekzamenatsionnye_voprosy_po_istorii.doc