Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кубанский государственный аграрный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ch_2_-_Pr-m_Gl_8-11

.pdf

Скачиваний:

Добавлен:

21.05.2015

Размер:

787.4 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Найти интеграл

I = ∫

− 9x 2

I = ∫

∫

d (3x)

arcsin 3x + C.

− (3x) 2

1 − (3x)2

10.4. Метод подстановки.

Интегрирование путем введения новой переменной (метод подстановки) основан на

формуле

∫ f (x)dx = ∫ f [ϕ (t)]ϕ ′(t)dt ,

где

x = ϕ (t)

–

дифференцируемая функция

переменной t.

Найти интеграл

I = ∫ xe x2 dx .

Положим x 2 = t ,

тогда 2xdx = dt,

xdx =

. Подставляя полученные значения в

подынтегральное выражение, получим

I = ∫ e x 2

xdx = ∫ et

∫ et dt =

+ C =

e x2 + C .

Этот пример можно решить и по-другому (см §2):

∫ xe x2 dx = ∫ e x2

xdx = ∫ e x2

d (x2 ) =

∫ e x 2 d (x2 ) =

e x2 + C .

Найти интеграл

I = ∫

cos x

dx .

+ 4 sin x

= t ,

1 + 4 sin x = t 2 , 4 cos xdx = 2tdt , cos xdx =

tdt.

Положим

1 + 4 sin x

откуда

Следовательно,

tdt

I = ∫

∫dt =

t + C =

+ C

1+ 4sin x

Найти интеграл

I = ∫ cos2 x sin xdx .

Положим

cos x = u ,

откуда

− sin xdx = du , sin xdx = −du

Таким образом,

I = ∫u 2 (−du) = −∫u 2 du = −

u 3

+ C =

cos3 x

+ C .

Тот же результат можно получить непосредственно (см §2):

∫ cos 2

x sin xdx = ∫ cos 2

xd (− cos x) = −∫ cos2

xd (cos x) = −

cos3 x

+ C .

I = ∫

4. Найти интеграл

подстановкой

x + 2 = t .

+ 2

+ 3

Из подстановки

= t следует, что x + 2 = t 2 ;

x = t 2

− 2 ;

dx = 2tdt , а поэтому

x + 2

подынтегральное выражение

t + 3 − 3

2tdt

;

I = ∫

= 2∫

dt = 2∫ 1 −

dt = 2[t − 3 ln

t + 3

]+ C .

x + 2 + 3

t + 3

Подставляя сюда t =

, окончательно получим

x + 2

I = 2(

− 3ln

+ 3

)+ C .

x + 2

Следует иметь в виду, что за счет тождественного преобразования ответа, а также в связи с возможностью представить произвольную постоянную интегрирования в разных видах ответы при вычислении неопределенных интегралов могут получаться различные.

Используя указанные замены переменной, найти интегралы:

10.21. ∫

10.22. ∫

(1 + x)dx

∫tg

, t = −

, t = 1

+ x .

10.23

dx, t = cos

1 / x

1 +

				dx
10.24. ∫						, t = 1e− x .
		e	x
					+ 1
10.27. ∫				1 + x 2			dx, x = tgt .
					x

		Найти интегралы:
10.28. ∫			dx

		e	2 x−1

10.31 ∫		dx
	3x + 1

			x		2
10.34. ∫					dx
		2x			3
					+ 5

10.37. ∫ e x 2 + 5e x dx

10.40. ∫ sin ln xdx x

10.43. ∫ 3 + 2x

x3 dx

10.46. ∫ 1 − x

xdx

10.49. ∫ 16 − x4

10.52. ∫ 2x + 1 dx

x2 + 1

10.55. ∫ x 2 + 2x + 1dx x 2 + 1

10.58. ∫ x + 2x 2 dx x 2 + 9

10.61. ∫

6x − x 2 − 5

10.64. ∫ 4x 2 + 12x + 13

10.67. ∫sin 4 x dx

10.70. ∫sin 2 2x

10.25. ∫		dx	, x =	1	.
10.25. ∫			, x =		.
	x	1 + x 2		t

10.29. ∫ 5 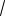3x + 2dx

10.32. ∫ 2 − x

10.35. ∫ (x + 1/ 4)sin(2x 2 + x)dx

10.38. ∫ 3 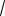2 + cos 3x sin 3xdx

10.41. ∫

arctgx / 3

9 + x

10.44. ∫

e− x dx

− e

−2 x

10.47. ∫

− 1

2x + 1

10.50. ∫

x 2 dx

+ 1

+ ln 2 x

10.53. ∫

10.56. ∫

35 x − 1

10.59. ∫

xdx

− 2

10.62. ∫

(2x − 3)dx

x 2

+ 4x + 5

10.65. ∫

xdx

− x 2 − 4x

10.68. ∫

sin 2x

10.71. ∫ 1 + cos 2 x sin 2xdx

10.26. ∫		x 2 dx	, x = sin t .

	1 − x 2

10.30. ∫

(4x + 3)

10.33. ∫

xdx

x 2

+ 2

10.36 ∫ e−

2 x

10.39 ∫ cos

2x + 1

10.42. ∫

+ 1

10.45. ∫

x 2 + 1

x + 1

10.48. ∫

− 5

10.51. ∫

+ 1

+ 2

10.54. ∫

x 2 dx

+ 3

10.57. ∫ x + arcsin xdx

1 − x 2

10.60. ∫ x 2 + 2x

10.63. ∫ x2 + 2x − 3

10.66. ∫ sin 2xdx

2 + cos2 x

10.69. ∫ ctg x + 3dx

10.72. ∫ (cos x)1/ 2 dx

(sin x)5 / 2

10.5. Метод интегрирования по частям.

Если u = ϕ1 (x) , v = ϕ2 (x) -дифференцируемые функции от x,			то из формулы для
дифференциала произведения двух функций	d (uv) = udv + vdu
получается формула интегрирования по частям
∫udv = uv − ∫ vdu		.	(18)

Эта формула применяется в случае, когда подынтегральная функция представляет произведение алгебраической и трансцендентной функции.

Вкачестве u обычно выбирается функция, которая упрощается дифференцированием, в качестве dv – оставшаяся часть подынтегрального выражения, содержащая dx, из которой можно определить v путем интегрирования.

Внекоторых случаях для сведения данного интеграла к табличному формула (18) применяется несколько раз. Иногда искомый интеграл определяется из алгебраического уравнения, получающегося с помощью интегрирования по частям.

1. Найти			I = ∫ x sin xdx .
Обозначим: x = u,			sinx dx = dv.
Для применения формулы (18) необходимо знать еще v и du. Дифференцируя
равенство x = u, получаем dx = du. Интегрируя равенство				dv = sin xdx = d (− cos x) ,
определяем v = − cos x .
Подставляя значения u, v, du, dv в формулу (18) находим
I = x(− cos x) − ∫ (− cos x)dx = −x cos x + sin x + C = sin x − x cos x + C .
2. Найти	u = x2		I = ∫ x 2 cos xdx .
Полагая	u = x2	,	dv = cos xdx = d (sin x) , получаем	du = 2xdx ,	v = sin x .
Следовательно,			I = x 2 sin x - ∫ sin x × 2xdx = x 2 sin x - 2∫ x sin xdx .
			I = x 2 sin x - ∫ sin x × 2xdx = x 2 sin x - 2∫ x sin xdx .		(А)
Полученный интеграл снова находится интегрированием по частям (пример 1). Его
можно найти и не вводя явно u и v. Имеем
∫ x sin xdx = ∫ xd (- cos x) = x(- cos x) - ∫ (- cos x)dx = -x cos x + sin x + C .
Подставляя это выражение для интеграла в формулу (А), находим
∫ x 2 cos xdx = x 2 sin x − 2∫ x sin xdx = x 2 sin x − 2(−x cos x + sin x + C1 ) =
= x 2 sin x + 2(x cos x − sin x) + C ,
где C = −2C1 .			1
где C = −2C1 .			I = ∫ e x sin xdx .
3. Найти			I = ∫ e x sin xdx .
Положим u = e x ,		dv = sin xdx , отсюда du = e x dx , v = − cos x .
Применяя формулу (18), получаем
	I = e x (− cos x) − ∫ (− cos)e x dx = −e x cos x + ∫ e x cos xdx .				(В)

К интегралу в правой части снова применяем формулу интегрирования по частям, не вводя явно u и v. Имеем

	∫ e x cos xdx = ∫ e x d (sin x) = e x sin x − ∫ e x sin xdx .
Подставляя найденное выражение в формулу (В), находим
	∫ e x sin xdx = −e x cos x + ∫ e x cos xdx = −e x cos x + e x sin x − ∫ e x sin xdx
	∫ e x sin xdx + ∫ e x sin xdx = e x sin x − e x cos x ,
откуда	2∫ e x sin xdx = e x (sin x − cos x) .

Следовательно,

∫ e x sin xdx =

e x

(sin x − cos x) + C.

Найти интегралы:

10.75. ∫ xe5 x dx

10.76. ∫ x 2 e− x / 2 dx

10.77. ∫ x3e2 x dx

10.79. ∫ (x 2

− 3x)ln xdx

10.80. ∫ x 2 ln 2 xdx

10.81. ∫

ln(1

−

d x

10.83. ∫

d x

10.84. ∫ x 2

− 4dx

10.85. ∫

2 − x 2 dx

cos

10.87. ∫ arctg

10.88 ∫

arcsin

10.89 ∫

x 2 cos

7x − 1

xdx

10.91. ∫ cos

(ln x)dx

10.92. ∫ e

10.93. ∫ ln(

)dx

x dx

1 − x

1 + x

10.95. ∫ xtg 2 2xdx

10.96. ∫ x ln

1 − x

10.97. ∫ cos 2 (ln x)dx

1 + x

arcsin x

10.99. ∫

10.100. ∫ (arcsin x)

10.101. ∫3x cos xdx

10.103. ∫ ln(1 + x 2 )dx

10.104. ∫

ln x

(x + 1)

10.78. ∫ ln(1 − x)dx

10.82. ∫ x sin 3xdx

10.86. ∫ x cos 2 xdx

10.90. ∫ e x sin x dx

∫ x cos x

10.94.

sin 2 x

10.98. ∫ x 2 arctg3xdx

10.102. ∫ e3x sin 2xdx

10.6. Интегрирование некоторых функций, содержащий квадратный трехчлен.

Интеграл вида		dx
	∫ px2	+ qx + r

путем дополнения квадратного трехчлена до полного квадрата по формуле px 2 + qx + r = p[(x + α )2 ± a 2 ]

сводится к одному из двух интегралов

∫

arctg

+ C;

(19)

∫

2 2

+ a

− a

где

u = x + α .

mx + n

Интеграл

∫

px 2

+ qx + r

сводится к интегралу (19) или (20) и интегралу

∫

udu

∫

(u 2 ± a

2 )

± a

+ C.

u 2 ± a2

u 2 ± a 2

Интеграл

∫

px 2 + qx + r

интегралов

1		u − a	+ C,	(20)
	ln
2a		u + a

(21)

(22)

сводится к одному из

	du	= arcsin	u	+ C; (23)
∫		= arcsin		+ C; (23)
∫	a 2 − u 2		a

Интеграл

сводится к одному из двух интегралов:

∫ u 2 + α du = u

∫

udu

= ln

u + u 2

+ a

+ C.

(24)

u 2 + a

∫

px 2 + qx + r

(25)

+ α ln

u +

+ C

u 2 + α

(26)

∫

du =

a 2

arcsin

+ C.

a 2 − u 2

(27)

1. Найти интеграл

I = ∫

+ 4x + 13

Дополняя квадратный трехчлен до полного квадрата и интегрируя на основании формулы (19) для случая когда u = x + 2, a = 3 , получаем

I = ∫

= ∫

∫

d (x + 2)

x + 2

+ C.

(x 2 + 4x + 4)+ 9

arctg

(x + 2)2 + 9

(x + 2)2 + 32

2. Найти интеграл

I = ∫

5 − 4x − x 2

Дополняя квадратный трехчлен до полного квадрата и интегрируя на основании формулы (23), получаем

I = ∫

= ∫

d (x + 2)

− (x 2 + 4x + 4 − 4 − 5)

5 − 4x − x 2

− (x + 2)2 + 9

32 − (x + 2)2

= arcsin

x + 2

+ C.

I = ∫

dx.

3. Найти интеграл

8 + 2x − x 2

Это интеграл вида (25). Преобразуя квадратный трехчлен и применяя формулу (27),

получаем

I = ∫

dx = ∫

dx =∫

dx =

8 + 2x − x 2

− (x 2 − 2x + 1 − 1 − 8)

− (x 2 − 2x + 1)+ 9

= ∫

d (x − 1) =

x − 1

arcsin

x − 1

+ C =

− (x − 1)2

x − 1

arcsin

+ C.

8 + 2x − x 2

Найти интегралы:

10.105. ∫

10.106. ∫

10.107. ∫

+ 36

+ 17

−

10.108. ∫

10.109. ∫

10.110. ∫

− 5х +

− х − 1

10х − 24

10.111. ∫

(х − 1)dх

10.112. ∫

10.113. ∫

+ 3х −

− х − 1

3х2 − 6х + 12

2х2

10.114. ∫

10.115. ∫

10.116. ∫

x 2

+ 4х + 13dx.

5 + 4x − x 2 dx.

х2

+ 2х

10.7. Интегрирование рациональных функций.

Неопределенный интеграл от целой рациональной функции (многочлена) находится непосредственно:

∫ (a0 + a1 x + ... + an x n )dx = a0 ∫ dx + a1 ∫ xdx + ... + an ∫ x n dx.

Интегрирование дробной рациональной функции сводится к интегрированию

правильной рациональной дроби

P(x)	,	(28)

Q(x)

Где P(x) и Q(x) - многочлены, причем степень P(x) ниже степени Q(x) .

Если же степень числителя равна степени знаменателя или больше ее, то

рациональная дробь называется неправильной.
	x3 + x 2	− 9		x5	− 3x 2 + x − 8
Дроби			и				-	неправильные:	в первой степень
	2x3 + 3x 2	− x + 7			x2 + x +	3

числителя равна степени знаменателя, а во второй степень числителя больше степени знаменателя.

Из неправильной рациональной дроби всегда можно выделить целую часть (многочлен). Это достигается делением числителя на знаменатель по правилу деления многочленов.

Всякая неправильная рациональная дробь может быть представлена в виде суммы многочлена и правильной дроби.

Поэтому интегрирование рациональной дроби всегда может быть приведено к

интегрированию многочлена и правильной дроби.

Если

многочлен

Q(x) имеет действительные

корни a, b,..., l соответственно

кратности α , β ,..., λ комплексные попарно сопряженные корни α k

± iβ k

(k = 1, 2,..., s)

соответственно кратности v1 , v2 ,..., v3 , т.е.

Q(x) = (x − a)α (x − b) β ...(x − l)

λ (x 2

+ p x + q )v1 (x 2 + p

x + q

)v2

...(x 2 + p

x + q

)vs ,

то справедливо следующее разложение дроби (28) на простейшие дроби:

P(x)

Aα

+ ... +

Q(x)

(x − a)

(x − a) 2

(x − a)α

(x − b)

(x − b)2

Bβ

Lλ

C1 x + D1

+ ... +

+ ...

(x − b) β

(x − l)

(x − l)2

(x − l)λ

x 2 + p x + q

(29)

C2 x + D2

+ ... +

Cv1 x + Dv1

+ ... +

M 1 x + N1

(x 2 + p1 x + q1 )2

2 + p x + q

)v1

x 2 + ps x + qs

M 2 x + N 2

+ ... +

Mvs x + Nvs

(x 2 + p

x + q

2 + p

x + q

)vs

Постоянные

A1 ,

A2 ,..., Aα , B1 , B2 ,..., Bβ , L1 , L2 ,..., Lλ , C1 ,

D1 ,..., M vs , N vs находятся

методом неопределенных коэффициентов.

После разложения на простейшие слагаемые интегрирование правильной рациональной дроби сводится к нахождению интегралов вида:

I1	=	∫	dx	;	(30)	I 2 =	∫	Mx + N	dx.	(31)
			(x − a)n					(x2 + px + q) m

Интеграл (30) находится по формуле (5′) , если n = 2, 3,..., или по формуле (6'), если n = 1.

Интеграл (31) при m = 1 является интегралом вида (21), при m > 1 применяется метод

понижения.	имеет действительный корень b , кратности β ,
3амечание 1. Если многочлен Q(x)
то по формуле (29) ему соответствует β	простейших слагаемых	Aμ	(μ = 1, 2,..., β ),
		(x − b)μ

каждое из которых равно дроби, числитель которой - постоянная, а знаменатель - соответствующая степень разности (x − b) , причем берутся все степени от 1 до β .

Замечание 2. Если многочлен Q(x) имеет комплексные попарно сопряженные корни

ak ± ibk кратности vk , то в разложении (29) им соответствует vk элементарных дробей вида

Следовательно,

− 3 x − 3

+ 1 x − 2

Решая эту систему, находим:

M μ x + N μ					(μ = 1, 2,..., vk ),
(x 2 + p	k	x + q	k	)μ

Числитель каждой из которых есть линейная функция (не постоянная как в

предыдущем случае), а знаменатель - степень соответствующего трехчлена, т.е. трехчлена x 2 + pk x + qk = [x − (ak + ibk )][x − (ak − ibk )],

причем берутся все степени от 1 до vk .

Замечание 3. Коэффициенты разложения (29) можно получить полагая в тождестве (29) или ему равносильном х равным надлежащим образом выбранным числам (метод произвольных значений).

1. Найти интеграл	I = ∫			9 − 5x
								dx.
		x	3	− 6x	2	+
							11x − 6

Разложим сначала правильную дробь

9 − 5x

x3 − 6x 2 + 11x − 6

на простейшие дроби, для чего нужно найти корни его знаменателя, т.е. корни уравнения

x3 − 6x 2 + 11x − 6 = 0.

Один корень находится методом подбора, это x1 = 1. Так как

(x3 − 6x 2 + 11x − 6): (x − 1) = x 2 − 5x + 6,

то

x3 − 6x 2

+ 11x − 6 = (x − 1)(x 2

− 5x + 6) = (x − 1)(x − 2)(x − 3),

поэтому получаем также

x2 = 2,

= 3.

Итак, многочлен имеет действительные простые корни

x1 = 1, x2 = 2, x3 = 3.

В соответствии с формулой (29) ищем разложение данной дроби на простейшие

9 − 5x

(А)

x3 − 6x 2 + 11x −

−

6 x − 1 x

2 x − 3

(Слагаемых вида

mx + n

разложение

не содержит, так как комплексных

(x 2

+ px + q)k

корней нет). Приводя дроби в правой части к общему знаменателю, получаем

9 − 5x

A(x − 2)(x − 3) + B(x − 1)(x − 3) + C(x − 1)(x − 2)

x3 − 6x 2 + 11x − 6

(x − 1)(x − 2)(x − 3)

Сравниваем числители

9 − 5x = A(x − 2)(x − 3) + B(x − 1)(x − 3) + C(x − 1)(x − 2).

(В)

Раскрывая скобки в правой части равенства (В) и группируя члены, находим

9 − 5x = (A + B + C )x 2 − (5A + 4B + 3C )x + (6 A + 3B + 2C ).

Сравнивая коэффициенты при одинаковых степенях x в обеих частях равенства,

получим три уравнения для определения неизвестных коэффициентов А, В, С: A + B + C = 0

5A + 4B + 3C = 5

6 A + 3B + 2C = 9 А = 2, В = 1, С = -3.

9 − 5x 2

x3 − 6x 2 + 11x − 6 x − 1

и поэтому

9 − 5x

I = ∫

dx = ∫

−

dx = 2∫

dx + ∫

− 6x

+11x − 6

x − 3

x −1

x − 2

x −1 x − 2

= 2∫ d (x −1) + ∫ d (x − 2) − 3∫ d (x − 3) = 2 ln x −1 + ln x − 2 − 3ln x − 3 + C.
x −1	x − 2	x − 3

dx − 3∫	1	dx =

	x − 3

Таким образом

∫

9 − 5x

dx = ln

(x − 1)2 (x − 2)

+ C.

x3 − 6x 2

+ 11x − 6

(x − 3)3

Замечание. Коэффициенты разложения (А) можно было бы найти, полагая в

равенстве (В)

x = 1, x = 2, x = 3. Действительно при

x = 1

имеем

9-5 = А(-1)(-2), 4 = 2А,

откуда А=2. Аналогично В = 1, С = -3.

Найти интеграл

I = ∫

x 2 dx

dx.

(x +

2)(x −

Подынтегральная функция является правильной рациональной дробью, знаменатель

которой

Q(x) = (x + 2)(x −1)2 имеет

простой корень

= 2

кратный

корень x

= 1

(кратности 2).

соответствии

формулой

(29)

разложение

подынтегральной

функции

на

простейшие дроби имеет вид

x 2

(x + 2)(x − 1)2

x + 2

x − 1

(x − 1)2

Откуда

x 2

= A(x − 1)2 + B(x − 1)(x + 2) + C(x + 2).

Полагая x = 1, получим 1 = C(1 + 2) , откуда C =

При x = −2 находим (−2) 2

= A(−2 − 1) 2 или 4 = 9 A , откуда A =

Полагая

x = 0 , получаем 0 = A(0 − 1) 2

+ B(0 − 1)(0 + 2) + C(0 + 2) или A − 2B + 2C = 0 .

Принимая во внимание значения А и С, из последнего уравнения находим B =

x 2

Следовательно,

(x + 2)(x − 1)2

x + 2

x − 1

(x − 1)2

поэтому

d (x + 2)

d (x −1)

I = ∫

x2 dx

∫

x + 2

x −1

−

+ C.

(x + 2)(x −

x + 2

x −1

(x −1)

3(x −1)

Итак,

I = ∫

x 2 dx

(x + 2)4 (x − 1)5

−

+ C.

+ 2)(x − 1)

3(x − 1)

Найти интегралы:

10.117. ∫

10.118. ∫

x 2

10.119. ∫

− x

− 2

− x

− x)

10.120. ∫

10.121. ∫

10.122. ∫

xdx

+ x

+ 1

− 1

10.123. ∫

10.124. ∫

10.125. ∫

(x 2 + 2)dx

(x 2 − 1)(x + 2)

x(x + 1)2

(x + 1)2 (x − 1)

10.126. ∫

xdx

10.127. ∫

x 2 − x

10.128. ∫

x3 + 1

+ 3x − 4

−

− 6x + 10

10.129. ∫

3x 2 + 8

10.130. ∫

10.131. ∫

x3 + 4x 2 + 4x

x 4 + x 2

x 4

+ 1

10.132. ∫

3x + 5

10.133. ∫

10.134. ∫

(x 2

+ 2x + 5)2

x 4 + x 2 + 1

(4 + x 2 )2

10.135. ∫

x3 − 3

10.136. ∫

10.137. ∫

+ 10x

+ 25

− 1

− 4x

+ 5x − 2

10.138. ∫

x 2 − x + 14

10.139. ∫

x8 + x6

(x − 4)3 (x − 2)

10.8. Интегрирование тригонометрических функций.

1. Интегралы вида

∫sin ax cos bxdx , ∫sin ax sin bxdx ,

∫ cos ax cos bxdx находятся

с помощью тригонометрических формул:

sin a sin b = 1 [cos(a − b) − cos(a + b)];cos a cosb = 1 [cos(a − b) + cos(a + b)];

2							2
sin a cosb =	1		[sin(a − b) + sin(a + b)].

2					I n,m = ∫sin n x cosm xdx ,
2. Интегралы вида								где n и m – четные числа,
находятся с помощью формул:
sin 2 x =		1		(1 − cos 2x); cos2 x =		1	(1 + cos 2x); sin x cos x =		1	sin 2x .

2					2			2

Если хотя бы одно из чисел n и m – нечетное, то интеграл находим непосредственно, отделяя от нечетной степени один множитель и вводя новую переменную. В частности, если m=2k+1, то

I n,m = ∫sin n x cos2k +1 xdx = ∫sin n x cos2k x cos xdx = ∫sin n x(1 − sin 2 x) k d (sin x).

3. Интегралы вида

∫ R(sin x, cos x)dx,

где R –

рациональная функция от

sin x и cos x , приводятся к интегралам от рациональных функций новой переменной с

помощью подстановки tg

= t , при этом sin x =

cos x =

1 − t 2

dx =

1 + t 2

+ t 2

1 + t 2

Если R(− sin x,− cos x) = R(sin x, cos x), то

целесообразно

применить

подстановку

tgx = t , при этом

sin x =

, cos x =

, dx =

+ t 2

1 . Найти интеграл

I = ∫sin 7x sin 3xdx.

Так как sin 7x sin 3x =

[cos(7 − 3)x − cos(7 + 3)x] =

(cos 4x − cos10x), то

∫sin 7x sin 3xdx =

∫[cos 4x − cos10x]dx =

∫ cos 4xdx − ∫ cos10xdx =

sin 4x −

sin10x + C.

2. Найти интеграл

I = ∫sin 3 xdx. .

Запишем, что sin 3 x = sin 2 x sin x = (1 − cos2 x)sin x. Тогда

I = ∫ (1 - cos2 x)sin xdx.

(А)

Применяя подстановку cos x = z , тогда − sin xdx = dz , получим

I = -∫ (1 - z 2 x)dz = -z +

z 3

+ C.

Возвращаясь к старой переменной, получим окончательно

I = - cos x +

cos3 x

+ C.

Собственно говоря, для вычисления интеграла (А) никакой подстановки не

требуется, так как формула

u n+1

∫u n u¢dx =

+ C

n +1

позволяет сразу написать ответ. Из (А) следует, что

I =

∫

sin xdx -

∫

cos 2

x sin xdx = - cos x +

cos2

x(-sin x)dx = - cos x +

cos3 x

+ C.

∫ 123

14243

u 2

u′

3. Найти

I = ∫

sin

Применим универсальную тригонометрическую подстановку:

= t;

sin x =

;

dx =

2dt

+ t 2

1 + t 2

Поэтому

2dt

1 + t

(1 + t

)

1 + 2t

+ t

1 1

I = ∫

∫

dt =

∫

+ t dt =

2 + 2 ln

+ C

2 t

(1 + t 3 )3

Возвращаясь к старой переменной: заменяя t

на tg

= -

tg 2

+ C = -

ctg 2

tg 2

+ C.

2 x

2 2

4. Найти интеграл

= ∫

5 cos

9 sin

(- sin x), cos x

Подынтегральная

функция

не

меняется

от

замены

sin x

на

− (cos x) , т.е.

R(− sin x,− cos x) = R(sin x, cos x)

Применяя подстановку tgx = t . Так как при этом

sin x =

cos x =

x = arctgt,

dx =

1 + t 2

+ t 2

то

1 + t 2

5 cos2 x + 9 sin 2

5 + 9t 2

5 cos2 x + 9 sin 2 x

+ 9t 2

Следовательно,

d (3t)

I = ∫

= ∫

3tgx

(

)2 + (3t )2

arctg

+ C =

arctg

+ C.

5 cos2 x + 9 sin 2 x

5 + 9t 2

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.05.2015665.6 Кб31A_Few_Glimpses_of_Ecology_metodichka.doc
#
21.05.20152.51 Mб88bibliofond.ru_732812.rtf
#
21.05.2015315.39 Кб25Bilety_po_filosofii.doc
#
02.12.2018205.31 Кб8biology.doc
#
21.05.2015357.59 Кб60Ch_1-_Pr-m_Gl_1-7.pdf
#
21.05.2015787.4 Кб46Ch_2_-_Pr-m_Gl_8-11.pdf
#
21.05.20152.94 Mб151Ch_2_-_Pr-m_Gl_8-11_-_kopia.doc
#
21.05.2015403.46 Кб16datyIstoria_Rossii.doc
#
21.05.2015720.45 Кб16Don_Failla_System.pdf
#
21.05.201537.89 Кб12Ekzamenatsionnye_voprosy_po_istorii.doc
#
21.05.2015182.52 Кб65EKZAMEN_bu.docx