
Biomechanics Principles and Applications - Schneck and Bronzino
.pdf
282 |
Biomechanics: Principles and Applications |
(b)
(c)
FIGURE 19.3 (continued) (b) Long time response for various M values. Note the small undershoot for M = 1, no conditions of an overdamped system were put on the model. As the system is highly overdamped this set of nondimensional parameters (M = 1, R = 0.75, and ε = 0.2) would not be an acceptable solution. (c) Short time response for various values of ε. Note that this elastic parameter does not have much effect on the otoconial layer maximum displacement for a step change in velocity solution. This is not true for a step change in acceleration, see part (f).
Starting with the nondimensional fluid and gel layer equations, taking the Laplace transform with respect to time and using the initial conditions give two ordinary differential equations. These equations can then be solved, using the boundary conditions. Taking the Laplace transform of the otoconial layer motion equation, combining with the two differential equation solutions, and integrating otoconial layer velocity to get deflection produces the transfer function for displacement reacceleration:

Vestibular Mechanics |
283 |
(d)
(e)
FIGURE 19.3 (continued) (d) Effect of the mass or density parameter R on response. R changes the maximum otoconial layer displacement. (e) Response to a step change in acceleration for various values of the damping parameter M. Note the overshoot for M = 1.
δo (s)= |
|
|
|
|
(1− R) |
|
|
|
|
|
(19.9) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Rs |
|
|
Rs |
|
|
|
|
s s + |
Rs + |
+ M |
|
|
|
coth |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
s |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
+ M |
|
|
+ M |
|
||
|
|
|
|
|
|
s |
s |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
284 |
Biomechanics: Principles and Applications |
(f)
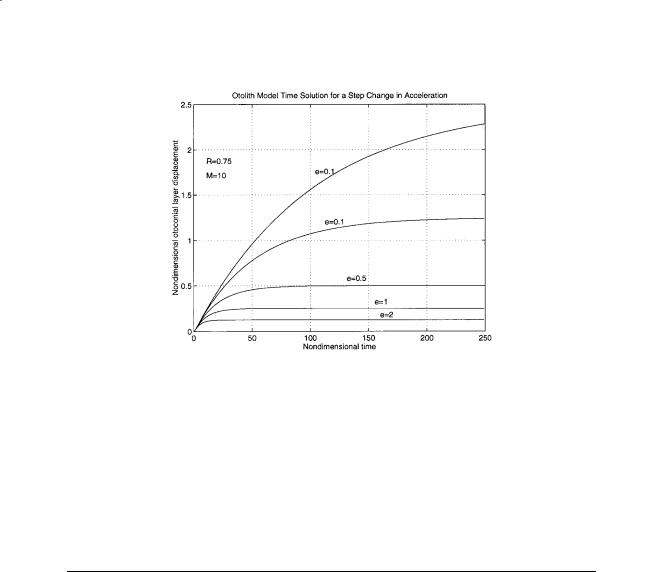
FIGURE 19.3 (continued) (f) Acceleration step change time response for various values of the elastic parameter ε. Note that this parameter affects the final displacement of the system for this type of constant stimulus (compare with part (c)).
where the overbars denoting nondimensional variables have been dropped, s is the Laplace transform variable, and a general acceleration term A is defined as:
|
∂V |
s |
|
|
A = − |
|
− g x |
(19.10) |
|
∂t |
|
|||
|
|
|
|
19.5 Otolith Frequency Response
This transfer function can now be studied in the frequency domain. It should be noted that these are linear partial differential equations and that the process of frequency domain analysis is appropriate. The range of values of ε = 0.01–0.2, M = 5–20, and R = 0.75 have been established by Grant and Cotton [1991] in a numerical finite difference solution of the governing equations. With these values established, the frequency response can be completed.
In order to construct a magnitudeand phase-vs.-frequency plot of the transfer function, the nondimensional time will be converted back to real time for use on the frequency axis. For the conversion to real time the following physical variables will be used: ρo = 1.35 g/cm3, b = 15 µm, µf = 0.85 mPa·s. The general frequency response is shown in Fig. 19.4. The flat response from DC up to the first corner frequency establishes this system as an accelerometer. These are the range-of-motion frequencies encountered in normal motion environments where this transducer is expected to function.
The range of flat response can be easily controlled with the two parameters ε and M. It is interesting to note that both the elastic term and the system damping are controlled by the gel layer, and thus an animal can easily control the system response by changing the parameters of this saccharide gel layer. The cross-linking of saccharide gels is extremely variable, yielding vastly different elastic and viscous properties of the resulting structure.
The otoconial layer transfer function can be compared to recent data from single-fiber neural recording. The only discrepancy between the experimental data and theoretical model is a low-frequency phase lead and accompanying amplitude reduction. This has been observed in most experimental single-fiber recordings and has been attributed to the hair cell.

Vestibular Mechanics |
285 |
FIGURE 19.4 General performance of the octoconial layer transfer function shown for various values of the nondimensional elastic parameter E and M. For these evaluations the other parameter was held constant and R = 0.75. The value of M = 0.1 shows an underdamped response which is entirely feasible with the model formulation, since no restriction was incorporated which limits the response to that of an overdamped system.
19.6 Semicircular Canal Distributed Parameter Model
The membranous SCC duct is modeled as a section of a rigid torus filled with an incompressible newtonian fluid. The governing equations of motion for the fluid are developed from the Navier–Stokes equations. Refer to the nomenclature section for definition of all variables, and Fig. 19.5 for a crosssection of the SCC and utricle.

286 |
Biomechanics: Principles and Applications |
FIGURE 19.5 Schematic structure of the semicircular canal showing a cross-section through the canal duct and utricle. Also shown in the upper right corner is a cross-section of the duct. R is the radius of curvature of the semicircular canal, a is the inside radius to the duct wall, and r is the spatial coordinate in the radial direction of the duct.
We are interested in the flow of endolymph fluid with respect to the duct wall, and this requires that the inertial motion of the duct wall RΩ be added to the fluid velocity u measured with respect to the duct wall. The curvature of the duct can be shown to be negligible since a R, and no secondary flow is induced; thus the curve duct can be treated as straight. Pressure gradients arise from two sources in the duct: (1) the utricle, (2) the cupula. The cupula when deflected exerts a restoring force on the endolymph. The cupula can be modeled as a membrane with linear stiffness K = ∆p/∆V, where ∆p is the pressure difference across the cupula and ∆V is the volumetric displacement, where:
∆V = 2π ∫t ∫a u(r,t )rdr dt |
(19.11) |
|
0 |
0 |
|
If the angle subtended by the membranous duct is denoted by β, the pressure gradient in the duct produced by the cupula is:
∂p |
= |
K∆V |
(19.12) |
|
|
||
∂z βR |
|
||
The utricle pressure gradient can be approximated [see Van Buskirk, 1977] by:
∂p |
= |
(2π − β) |
ρRα |
(19.13) |
|
∂z |
β |
||||
|
|
|
When this information is substituted into the Navier–Stokes equation, the following governing equation for endolymph flow relative to the duct wall is obtained:
∂u |
|
2π |
|
2πK |
|
t |
a |
1 |
+ |
Rα = − |
|
|
u (rdr)dt + v |
||||
|
β |
ρβR ∫0 |
∫0 |
|
||||
∂t |
|
|
r |
|||||
∂ |
|
∂u |
|
|
|
r |
|
|
(19.14) |
|
|
|||
∂r |
∂r |
|
||

Vestibular Mechanics |
287 |
This equation can be nondimensionalized using the following nondimensional variables denoted by overbars:
|
|
|
r |
|
v |
|
|
|
u |
|
|
|
r |
= |
|
t = |
|
|
t |
u |
= |
|
(19.15) |
|
a |
|
2 |
RΩ |
|||||||
|
|
|
a |
|
|
|
|||||
where Ω is a characteristic angular velocity of the canal. In terms of the nondimensional variables, the governing equation for endolymph flow velocity becomes:
|
|
|
|
|
|
α(t )= − |
t |
1 |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∂u |
+ |
2π |
|
∫0 |
∫0 |
|
|
|
|
|
|||||
u |
rdr |
||||||||||||||
|
β |
||||||||||||||
∂t |
|
|
|
|
|
|
|
|
|||||||
where the nondimensional parameter ε is defined by:
= 2Kπa6
ρβRv2
The boundary conditions for this equation are as follows:
)dt + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
∂ |
|
|
∂u |
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
r |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
r |
|
∂r |
|
∂r |
|||||||||
u (1, t )= 0 ∂∂ur (0, t )= 0
(19.16)
(19.17)
and the initial condition is u(r,0) = 0.
19.7 Semicircular Canal Frequency Response
To examine the frequency response of the SCC, we will first get a solution to the nondimensional canal equation for the case of a step change in angular velocity of the skull. A step in angular velocity corresponds to an impulse in angular acceleration, and in dimensionless form this impulse is:
α(t )= −Ωδ(t ) |
(19.18) |
where δ(t) is the unit impulse function and Ω is again a characteristic angular velocity of the canal. The nondimensional volumetric displacement is defined as:
φ = ∫t ∫1( |
|
|
|
|
|
)dt |
(19.19) |
|
u |
rdr |
|
||||||
0 |
0 |
|
|
|
|
|
|
|
the dimensional volumetric displacement is given by ∆V = (4πRΩa4/v)φ and the solution (for ε 1) is given by:
∞ |
2 2π β |
) |
|
|
φ = ∑ |
( |
|
(19.20) |
|
|
4 |
|
||
n =1 |
|
λπ |
|
|
288 |
Biomechanics: Principles and Applications |
where λn represents the roots of the equation J0(x) = 0, where J0 is the Bessel function of zero order (λ1 = 2.405, λ2 = 5.520), and for infinite time φ = π/8β. For details of the solution see Van Buskirk and Grant [1987] and Van Buskirk and coworkers [1978].
A transfer function can be developed from the previous solution for a step change in angular velocity of the canal. The transfer function of mean angular displacement of endolymph θ related to ω, the angular velocity of the head, is:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
(s)= s (2π |
β)λ1 |
|
|
|
|
1 |
|
|
|
|
(19.21) |
||
ω |
|
|
|
|
|
|
|
||||||
|
8 |
|
|
|
1 |
|
1 |
|
|
||||
|
|
|
|
|
|
s + |
|
s + |
|
|
|
||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
τL |
|
τs |
|
|||
where τL = 8ρvβR/Kπa4, τs = a2/λ21v, and s is the Laplace transform variable.
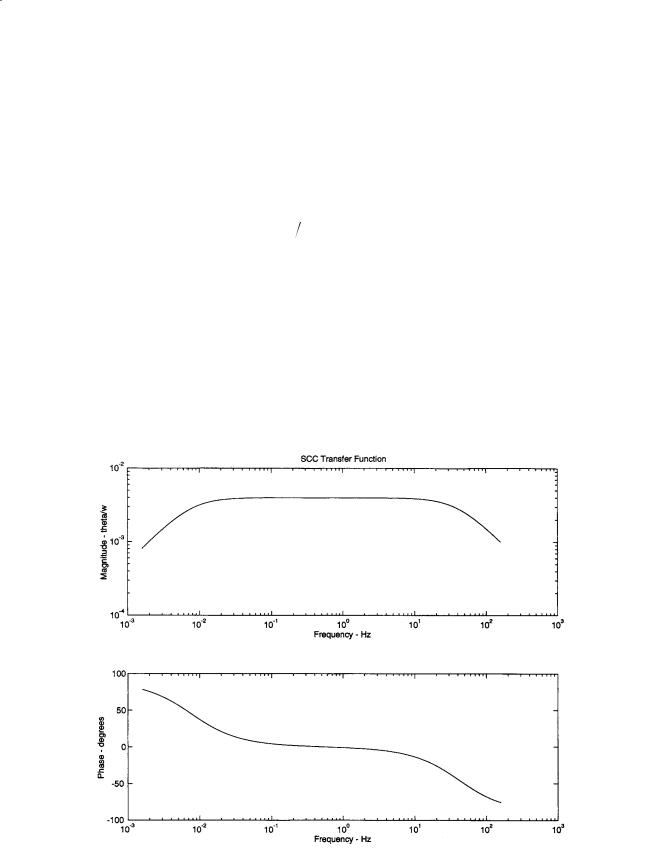
The utility of the above transfer function is apparent when used to generate the frequency response of the system. The values for the various parameters are as follows: a = 0.15 mm, R = 3.2 mm, the dynamic viscosity of endolymph µ = 0.85 mPa·s (v = µ/ρ), ρ = 1000 kg/m3, β = 1.4π, and K = 3.4 GPa/m3. This produces values of the two time constants of τL = 20.8 s and τs = 0.00385 s. The frequency response of the system can be see in Fig. 19.6. The range of frequencies from 0.01 Hz to 30 Hz establishes the SCCs as angular velocity transducers of head motion. This range of frequencies is that encountered in
FIGURE 19.6 Frequency response of the human semicircular canals for the transfer function of mean angular displacement of endolymph fluid θ related to angular velocity of the head w.

Vestibular Mechanics |
289 |
everyday movement. Environments such as an aircraft flight can produce frequencies outside the linear range for these transducers.
Rabbit and Damino [1992] have modeled the flow of endolymph in the ampulla and its interaction with a cupula. This model indicates that the cupula in the mechanical system appears to add a highfrequency gain enhancement as well as phase lead over previous mechanical models. This is consistent with measurements of vestibular nerve recordings of gain and phase. Prior to this work this gain and phase enhancement were thought to be of hair cell origin.
Defining Terms
Endolymph: Fluid similar to intercellular fluid (high in potassium) which fills the membranous labyrinth, canals, utricle, and saccule.
Kelvin–Voight viscoelastic material: The simplest of solid materials which have both elastic and viscous responses of deformation. The viscous and elastic responses appear to act in parallel.
Otolith: Linear accelerometers of the vestibular system whose primary transduced signal is the sum of linear acceleration and gravity in the frequency range from DC (static) up to the maximum experienced by an animal.
Semicircular canals: Angular motion sensors of the vestibular system whose primary transduced signal is angular velocity in the frequency range of normal animal motion.
References
Grant JW, Cotton JR. 1991. A model for otolith dynamic response with a viscoelastic gel layer. J Vestibular Res 1:139.
Grant JW, Best WA, Lonegro R. 1984. Governing equations of motion for the otolith organs and their response to a step change in velocity of the skull. J Biomech Eng 106:203.
Grant JW, Huang CC, Cotton JR. 1994. Theoretical mechanical frequency response of the otolith organs.
J Vestibular Res 4(2):137.
Lewis ER, Leverens EL, Bialek WS. 1985. The Vertebrate Inner Ear, Boca Raton, FL, CRC Press.
Rabbit RD, Damino ER. 1992. A hydroelastic model of macromachanics in the endolymphatic vestibular canal. J Fluid Mech 238:337.
Van Buskirk WC. 1977. The effects of the utricle on flow in the semicircular canals. Ann Biomed Eng 5:1. Van Buskirk WC, Grant JW. 1973. Biomechanics of the Semicircular Canals, pp. 53–54, New York, Bio-
mechanics Symposium of American Society of Mechanical Engineers.
Van Buskirk WC, Grant JW. 1987. Vestibular mechanics. In R. Skalak, S. Chien (Eds.), Handbook of Bioengineering, pp. 31.1–31.17, New York, McGraw-Hill.
Van Buskirk WC, Watts RG, Liu YU. 1976. Fluid mechanics of the semicircular canal. J Fluid Mech 78:87.
Nomenclature
Otolith Variables
x = coordinate direction in the plane of the otoconial layer
yg = coordinate direction normal to the plane of the otolith with origin at the gel base yf = coordinate direction normal to the plane of the otolith with origin at the fluid base t = time
u(yf,t) = velocity of the endolymph fluid measured with respect to the skull v(t) = velocity of the otoconial layer measured with respect to the skull
w(yg,t) = velocity of the gel layer measured with respect to the skull δg(yg,t) = displacement of the gel layer measured with respect to the skull
δo = displacement of the otoconial layer measured with respect to the skull
Vs = skull velocity in the x direction measured with respect to an inertial reference frame V = a characteristic velocity of the skull in the problem (magnitude of a step change)

290 |
Biomechanics: Principles and Applications |
ρo |
= density of the otoconial layer |
ρf |
= density of the endolymph fluid |
τg |
= gel shear stress in the x-direction |
µg |
= viscosity of the gel material |
µf |
= viscosity of the endolymph fluid |
G |
= shear modulus of the gel material |
b |
= gel layer and otoconial layer thickness (assumed equal) |
gx |
= gravity component in the x-direction |
Semicircular Canal Variables
u(r,t) = velocity of endolymph fluid measured with respect to the canal wall r = radial coordinate of canal duct
a = inside radius of the canal duct
R = radius of curvature of semicircular canal ρ = density of endolymph fluid
v = endolymph kinematic viscosity
ω = angular velocity of the canal wall measured with respect to an inertial frame
α = angular acceleration of the canal wall measured with respect to an inertial frame K = pressure-volume modulus of the cupula = ∆p/∆V
∆p = differential pressure across the cupula
∆V = volumetric displacement of endolymph fluid
β = angle subtended by the canal in radians (β = π for a true semicircular canal)
λn = roots of Jo(x) = 0, where Jo is Bessel’s function of order 0 (λ1 = 2.405, λ2 = 5.520)

A
Abdomen impact and injury acceleration-induced, 120–121 biomechanical responses, 124–127 blunt trauma, 120 compression-induced, 121–122 force-induced, 121
mechanisms of, 119–120 risk assessments, 127–128
viscous mechanism of, 122–124 Accelerometry, 133
Acetabular fossae, 42 Acetabulum, 42 Acromioclavicular joint, 52 Actin filament, 105 Adenosine diphosphate, 141
Adenosine monophosphate, 142 Adenosine triphosphate, 141, 151, 173 Afterload, 143
Ampulla, 278
Anabolic steroids, 157–158, 160 Anaerobic threshold, 149 Aneurysm, 213
Angiogenesis, 219, 224 Angle of anteversion, 42 Anisotropy
blood vessels, 30–33 definition of, 10
Ankle
anatomy of, 36 articulating surfaces of, 36 axes of rotation, 37, 39 contact of, 37
Anthropomorphic test devices, 116 Aortic valve
anatomy of, 189
blood flow parameters, 193 dimensions of, 190 dynamics of, 193
elastin fibers, 191
fibrous annular ring of, 190 leaflets of, 189, 192
marker fluoroscopy evaluations of, 192 mechanical properties of, 191–192 peak velocity of, 193
pressure levels in, 189 Apatite, 1, 15
Index
Apparent viscosity definition of, 217, 224 leukocytes, 234–236
Arches of Corti, 263
Area expansivity modulus, 228, 230, 236 Arterial circulation
blood flow characteristics, 206–208 blood vessels, see Blood vessels description of, 205
geometrical parameters of, 205–206 velocity profiles, 210–212
wave propagation, 208–210 Arterial impedance, 211, 213 Arterioles
blood flow of, 219 definition of, 143 diameter of, 218
oxygen transport, 220–221 vascular tone of, 217 viscoelastic behavior of, 218 walls of, 217
Arthritis, 87–89 Articular cartilage, 79 Atherosclerosis, 212–213
Atlanto-occipital joint, 108 Atomic force microscopy, 9
Axisymmetric deformation, 23–25, 228
B
B lymphocytes, 233 Baroreceptor reflex, 246 Basilar membrane
anatomy of, 262–263 sensitivity of, 268
Biceps muscle, 160 Biotribology, see also Tribology
arthritis and, 87–89 definition of, 73, 80 in vitro studies, 91
Blood
arterial elasticity effects, 208
colloid osmotic pressure of, 248–249, 257 composition of, 206, 216
red blood cell volumes in, 216, see also Red blood cells
Blood doping, 158 Blood flow
arteriolar, 219
