
матан
.pdf
8. Бесконечно большие и бесконечно малые ф ункции
Определение 8.1. Функция α(x) называется бесконечно большой при x ® x0 , если для любого положительного числа N существует положительное
число δ = δ(N ) |
такое, |
что для всехx , удовлетворяющих |
неравенству |
| x - x0 |< δ , выполняется неравенство | α(x) |> N. |
|
||
Обозначают lim α(x) = ¥. |
|
||
|
x®x0 |
|
|
Другими |
словами, |
функция α(x) называется бесконечно |
большой при |
x ® x0 , если значения функции α(x) неограниченно возрастают по абсолютной величине при неограниченном приближении x к x0 , где x ¹ x0 .
Определение 8.1 формально можно записать следующим образом:
("N > 0 |
$δ= δ(N ) > 0 "x ¹ x0 :| x - x0 |
|< δ Þ | α(x) | > N ) Û =lim α(x) ¥. |
|
|
x®x0 |
Следовательно, lim α(x) = ¥ тогда и только тогда, когда для любого по-
x®x0
ложительного числа N найдется такая δ − окрестность точки x0 , что для любого x ¹ x0 из этой δ − окрестности соответствующее значение функции α(x) по-
падает в интервал (-¥;-N ) |
|
или в интервал (N;+¥) . |
|||||||
y |
|
|
|
|
|
|
|
|
|
f (x1) |
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
y = N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = f (x) |
O x |
|
- δ x |
|
x |
|
x |
x |
|
x |
0 |
2 |
0 |
0 |
+ δ |
|||||
|
|
|
1 |
|
|
||||
y = -N
-N
f (x2 )
Рис. 8.1. Геометрический смысл предела lim f (x) = ¥
x®x0
График функции y = f (x) расположен выше прямой y = N или ниже прямой y = -N для любого x из δ − окрестности точки x0 (см. рис. 6.1). В этом
состоит геометрический смысл предела lim f (x) = ¥ .
x®x0
21
Например, функция α(x) = |
|
1 |
|
будет бесконечно большой при x ®1. |
x |
|
|
||
|
-1 |
|||
Определение 8.2. Функция |
|
α(x) называется бесконечно большой при |
||
x ® ¥ , если для любого положительного числа N существует положительное число M = M (N ) такое, что для всех x , удовлетворяющих неравенству | x | > M , выполняется неравенство | α(x) |> N.
Обозначают lim α(x) = ¥.
x®¥
Другими словами, функция α(x) называется бесконечно большой, если значения функции α(x) неограниченно возрастают по абсолютной величине
при x ® ¥ .
Определение 8.2 формально можно записать следующим образом:
("N > 0 $M= |
M (N ) > 0 "x :| x | > M Þ | α(x) | > N ) Û =lim α(x) ¥. |
||
|
|
|
x®x0 |
Следовательно, |
lim α(x) = ¥ тогда и только тогда, |
когда для любого по- |
|
|
|
x®¥ |
|
ложительного |
числа N найдется такое положительное |
числоM = M (N ) , что |
|
для любого x |
из интервала (-¥; M ) или (M ;+¥) соответствующее значение |
||
функции α(x) |
попадает в интервал (-¥;-N ) или в интервал (N;+¥) . |
||
y
y = f (x)
f (x1)
|
N |
y = N |
|
|
|
|
|
x |
x2 -M |
O |
M x1 |
-N
y = -N
f (x2 )
Рис. 8.2. Геометрический смысл предела lim f (x) = ¥
x®¥
22
График функции y = f (x) |
расположен |
выше |
прямой y = N или ниже |
прямой y = -N при x ® ¥ (см. |
рис. 8.1). В |
этом |
состоитгеометрический |
смысл предела lim f (x) = ¥.
x®¥ |
|
Например, функция α(x) = x2 |
будет бесконечно большой при x ® ¥ . |
Аналогично определяются |
бесконечно большие функции приx ® +¥ , |
x ® -¥ , x ® x0 - , x ® x0 + . |
|
Определение 8.3. Если lim α(x) = 0 , то α(x) называется бесконечно ма-
x®x0
лой функцией при x ® x0 .
Другими словами, функция α(x) называется бесконечно малой, если значения функции α(x) неограниченно приближаются к нулю при x ® x0 .
Аналогично определяются бесконечно малые функции xпри® ¥ , x ® +¥ , x ® -¥ , x ® x0 - , x ® x0 + .
Например, функция α(x) = x3 -1 является бесконечно малой при x ®1.
Рассмотрим свойства бесконечно малых функций.
Свойство 8.1. Сумма или разность конечного числа бесконечно малых функций есть бесконечно малая функция.
Свойство 8.2. Произведение бесконечно малой функции на ограниченную есть бесконечно малая функция.
Свойство 8.3. Произведение бесконечно малой функции на число есть бесконечно малая функция.
Свойство 8.4. Произведение конечного числа бесконечно малых функций есть бесконечно малая функция.
Свойство 8.5. Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть бесконечно малая функция.
Теорема 8.1. Если α(x) − бесконечно малая функция приx ® x0 , то
функция |
1 |
является бесконечно большой при x ® x0 . |
|
α(x) |
|||
|
|
||
|
|
9. Основные теоремы о пределах |
При нахождении пределов используются следующие теоремы о пределах.
Теорема 9.1. Если lim f (x) = A , lim g(x) = B , тогда
x®¥ |
x®¥ |
1) lim( f (x) ± g(=x)) A ± B; |
|
x®x0 |
|
23
2) lim ( f (x) × g(=x)) A × B;
x®x0
|
|
|
3) |
lim |
f (x) |
= |
A |
, при условии, что lim g(x) ¹ 0; |
|
||||||||||||
|
|
|
|
B |
|
||||||||||||||||
|
|
|
|
x®x0 g(x) |
|
|
|
|
|
|
|
|
x®x0 |
|
|||||||
|
|
|
4) lim c × f =(x) |
|
|
c × lim f (x). |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x®x0 |
|
|
x®x0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Замечание. |
Теорема 9.1 справедлива при x ® ¥ . Условия |
теоремы 9.1 |
||||||||||||||||
справедливы для любого конечного числа функций. |
|
||||||||||||||||||||
|
|
|
При нарушении условий теоремы 9.1 могут возникнуть неопределенности |
||||||||||||||||||
ì¥ |
ü, |
ì |
0 |
ü, {¥ - ¥}, |
{0 ×¥}, 1¥ |
} |
, |
которые в простейших случаях раскрывают- |
|||||||||||||
í |
|
í |
|
||||||||||||||||||
|
ý |
|
ý |
|
|
{ |
|
|
|
|
|
|
|
|
|
|
|||||
î¥ |
þ |
î |
0 þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ся с помощью алгебраических преобразований. |
|
||||||||||||||||||||
|
|
|
Теорема 9.2. Первый замечательный предел: |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
sin x |
=1. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x®0 |
x |
|
|||||
|
|
|
Теорема 9.3. Второй замечательный предел: |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
1 |
ö |
x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim (1 + x)x = e. |
|
||||||
|
|
|
|
|
|
|
|
|
|
lim |
ç1 |
+ |
|
÷ |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x®¥ è |
|
|
x ø |
|
x®0 |
|
|||||
|
|
|
Определение 9.1. Бесконечно |
малые функцииα(x) и β(x) |
называются |
||||||||||||||||
эквивалентными при x ® x , если lim |
α(x) |
=1, тогда пишут α(x) β(x). |
|
|
|||
0 |
x®x0 |
β(x) |
|
|
|
||
Теорема 9.4. Предел произведения(частного) двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой функцией.
Таким образом, эквивалентные бесконечно малые функции можно заменять друг на друга при вычислении предела произведения или частного, при этом нужно заменятьполностью либо один сомножитель, либо числитель и (или) знаменатель дроби. Заменять одно из слагаемых в сумме(или разности) нельзя.
Следующая таблица эквивалентных бесконечно малых функцийявля-
ется следствием теорем о пределах (здесь α(x) β(x) при x ® x0 ). |
|
|||
|
|
Эквивалентные бесконечно малые функции |
Таблица |
|
|
№ |
Бесконечно малая |
Эквивалентная |
|
|
п/п |
функция |
функция |
|
|
|
|
|
|
1 |
sin α(x) |
α(x) |
|
|
|
2 |
tg α(x) |
α(x) |
|
|
3 |
arcsin α(x) |
α(x) |
|
|
4 |
arctg α(x) |
α(x) |
|
24

|
|
|
|
|
|
|
Продолжение табл. |
5 |
1 - cos2 α(x) |
|
|
|
|
1 |
× α2 (x) |
|
|
|
2 |
||||
|
|
|
|
|
|
||
6 |
ln(1 + α(x)) |
|
|
|
|
|
α(x) |
7 |
eα( x ) -1 |
|
|
|
|
|
α(x) |
8 |
loga (1 + α(x)) |
|
|
|
α(x) ×loga e |
||
9 |
bα( x ) -1 |
|
|
|
|
α(x) ln b |
|
10 |
(1 + α(x))k -1 |
|
|
|
|
k ×α(x) |
|
Пример 9.1. Найти предел lim |
2x2 |
- x -1 |
. |
|
|
||
|
|
|
|
|
|||
|
x®1 x2 + 2x - 3 |
|
|
|
|||
Решение. При x ®1 предел числителя и знаменателя равен нулю. Следовательно, непосредственное применение теоремы9.1 здесь невозможно. Вы-
ì0 ü
числение данного предела сводится к раскрытию неопределенности видаí ý.
î0 þ
Для этого преобразуем дробь, разложив числитель и знаменатель на множители:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
1 ö |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2x |
2 |
- x -1 |
|
|
2(x -1) |
ç x + |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
= |
|
|
è |
|
|
|
2 ø |
. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x2 + 2x - 3 |
(x -1)(x + 3) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Разделим числитель и знаменатель на x -1 ¹ 0 . Это сокращение допусти- |
||||||||||||||||||||||||||||||||
мо, так как x ®1, но x ¹1. Поэтому для всех x ¹1 имеем |
2x2 |
- x -1 |
|
= |
|
2x +1 |
, и |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
x2 + 2x - 3 |
|
x + 3 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
пределы этих функций равны между собой. Таким образом, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
1 |
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x2 - x -1 |
ì0 |
ü |
|
|
|
2(x -1) |
ç x + |
|
|
÷ |
|
|
|
lim (2x +1) |
3 |
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||
lim |
|
|
= í |
|
|
ý |
lim |
= |
è |
|
|
|
ø |
= |
|
x®1 |
|
= |
|
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||||||||||||||||||
x®1 x2 + 2x - 3 |
î0 |
þ |
x®1 |
(x -1)(x + 3) |
|
|
|
|
|
lim (x + 3) |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x®1 |
|
|
|
|
|
|
|
|
|
Пример 9.2. Найти предел lim |
15x2 + 7x |
- 4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
x®+¥ 3x2 - 2x + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Непосредственное применение теоремы 9.1 здесь также невозможно, так как при x ® ¥ числитель и знаменатель стремятся к ¥ . В этом случае вычисление данного предела сводится к раскрытию неопределенности вида
ì¥ ü í ý. Для этого преобразуем дробь: разделим числитель и знаменатель на
î¥ þ
старшую степень x , то есть на x2 . Получим
25

lim |
15x2 |
+ 7x - 4 |
|
ì |
¥ |
ü |
|
|
= |
í |
|
= |
|
|
|
|
||||
x®+¥ 3x2 - 2x + 3 |
|
¥ |
ý |
|||
|
î |
þ |
||||
|
|
|
|
7 |
|
|
4 |
|
æ |
|
|
|
7 |
|
4 ö |
|
|
|
||||||||||||
|
15 + |
- |
|
|
|
lim ç15 |
+ |
|
|
|
- |
|
|
|
|
÷ |
15 |
|
||||||||||||
|
|
|
|
x |
|
x |
2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
lim= |
= |
|
x |
= |
|
x2 |
|
|
x®+¥ è |
|
|
|
|
|
|
|
ø |
5. |
||||||||||||
|
|
|
|
|
|
|
2 |
|
|
3 |
|
ö |
|
3 |
||||||||||||||||
x®+¥ |
3 - |
2 |
|
+ |
3 |
|
|
|
lim |
æ |
3 |
- |
|
+ |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
÷ |
|
|
|
||||||||||
|
x |
x |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
x |
x |
2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
x®+¥ |
è |
|
|
|
|
|
|
ø |
|
|
|
|||||||||||
Пример 9.3. Найти предел lim 1 - cos 6x . x®0 tg2 2x
Решение. При x ® 0 предел числителя и знаменателя равен нулю. Имеем
ì0 ü
неопределенность вида í ý. Для вычисления данного предела используем эк-
î0 þ
вивалентные бесконечно |
малые функции, а |
именно: |
1 - cos2 α(x) |
1 |
α2 (x) и |
|||||||||||||||||
2 |
||||||||||||||||||||||
tg α(x) α(x) . Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 - cos 6x |
ì0 ü |
1 |
×(6x) |
2 |
|
|
|
18x2 |
|
9 |
9 |
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||
lim |
|
|
|
= í |
=ý =lim |
= |
= |
|
= |
lim |
|
lim |
|
|
|
4,5. |
||||||
|
tg2 2x |
|
|
|
|
|||||||||||||||||
x®0 |
|
î0 þ x®0 |
|
|
(2x)2 |
|
|
|
x®0 4x2 |
x®0 2 2 |
|
|
|
|||||||||
|
|
|
|
|
æ x - 3 öx-1 |
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 9.4. Найти предел limç |
|
|
|
÷ . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
x®¥ è x +1 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. |
Здесь при x ® +¥ предел |
основания равен1, а показателя к |
||||||||||||||||||||
|
|
|
|
|
|
|
|
{ |
|
|
} |
. |
|
|
|
|
|
|
|
|
||
+ ¥ , то есть имеем неопределенность вида 1¥ |
|
|
|
|
|
|
|
|
|
|||||||||||||
1-й способ. Вычислим данный предел с помощью второго замечательного предела. Для этого преобразуем функцию – прибавим и вычтем 1:
|
|
|
|
|
|
x - 3 |
=1 + |
x - 3 |
-1 =1 + |
-4 |
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
x +1 |
|
|
x +1 |
|
|
|
x +1 |
|
|
|
|||||||
После преобразований получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x+1 |
|
|
×( x-1) |
|
æ x - 3 ö |
x-1 |
|
|
|
|
|
|
x-1 |
æ |
|
|
|
|
|
öx+1 |
||||||||
æ |
|
-4 ö |
æ |
|
-4 ö -4 |
|
|||||||||||||||||
¥ |
|
|
|
ç |
|
|
÷ |
|
|
||||||||||||||
limç |
|
÷ |
= {1 } |
lim=ç1 |
+ |
|
|
|
÷ |
= lim |
ç |
ç1 |
+ |
|
÷ |
|
|
= |
|
||||
|
|
x +1 |
|
|
|||||||||||||||||||
x®¥ è x +1 |
ø |
|
x®¥ è |
|
|
ø |
|
x®¥ |
è |
|
x +1 ø |
÷ |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
ø |
|
|
|
lim |
-4 x+4 |
-4 |
|
x®¥ |
x+1 |
||
e . |
|||
e= |
|
2-й способ. Вычислим данный предел с помощью эквивалентных бесконечно малых функций. Обозначим
æ x - 3 öx-1 A = ç ÷ .
è x +1 ø
Прологарифмируем левую и правую части данного равенства по основанию e :
æ x - 3 öx-1 ln A = ln ç ÷ ,
è x +1 ø
тогда
26

|
|
|
|
|
|
|
|
|
|
|
æ x - 3 ö |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
ln A = (x -1) ln ç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
или |
|
|
|
|
|
|
|
|
|
|
è x +1 ø |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 ö |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ln A = (x - |
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1)ln ç1 |
+ |
|
|
|
|
÷. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x +1 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|||
|
æ |
-4 |
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция ln ç1 + |
|
|
|
÷ является бесконечно малой при x ® ¥ и эквива- |
||||||||||||||||||||||
|
x +1 |
||||||||||||||||||||||||||
|
è |
ø |
|
|
-4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
лентна бесконечно малой функции |
|
при x ® ¥ . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x +1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Вычислим предел ln A при x ® ¥ : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||
|
|
æ |
|
|
-4 ö |
|
|
|
|
-4(x -1) |
ì¥ |
ü |
|
-4 + |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
lim ln A = lim(x -1) ln |
1 + |
|
={¥ ×0} |
|
lim= |
lim |
= x |
-4 . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
í |
|
= |
|||||||||||||
ç |
|
÷ |
|
|
|
|
|
|
|
|
|||||||||||||||||
x®¥ |
x®¥ |
è |
|
|
x +1 ø |
|
|
|
x®¥ |
|
|
x |
+1 |
|
|
|
î¥ |
þ |
x®¥ |
1 + |
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x
Следовательно, ln A ® -4 при x ® ¥ . Тогда, по определению логарифма и в силу монотонности логарифмической функции, получаем, что A ® e-4 , то есть
x-1
lim A = limæç x - 3 ö÷ = e-4 .
x®¥ x®¥ è x +1 ø
Пример 9.5. Найти предел lim (
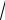 x + 2 -
x + 2 - 
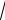 x - 2).
x - 2).
|
|
|
|
|
|
|
|
|
|
|
|
|
x®+¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Решение. Непосредственное применение теоремы 9.1 здесь |
невозможно, |
||||||||||||||||||||||||||||||||||||||||
так как при x ® +¥ выражения |
|
|
|
|
и |
|
|
|
|
стремятся к ¥ . В этом случае |
||||||||||||||||||||||||||||||||
|
x + 2 |
x - 2 |
||||||||||||||||||||||||||||||||||||||||
вычисление данного предела |
сводится |
|
|
к раскрытию |
неопределенности вида |
|||||||||||||||||||||||||||||||||||||
{¥ - ¥} . |
Для этого преобразуем функцию: умножим и разделим на выражение |
|||||||||||||||||||||||||||||||||||||||||
|
|
+ |
|
|
|
, сопряженное данному выражению |
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
. Получим |
|||||||||||||||||||||
|
x + 2 |
x - 2 |
x + 2 |
x - 2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
- |
|
|
|
|
)( |
|
|
|
+ |
|
|
) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 2 |
x - 2 |
x + 2 |
x - 2 |
|||||||||||||||||||||
|
lim ( |
|
|
x + 2 - x - 2) |
{¥ - ¥} lim |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
||||||||||||||||||
|
x®+¥ |
|
|
|
|
|
|
|
|
|
|
|
|
x®+¥ |
|
|
|
|
|
|
x + 2 + x - 2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
= lim |
|
4 |
|
|
|
|
|
= |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
=0. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x + 2 + |
|
|
x - 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
x®+¥ |
|
|
|
lim ( x + 2 + x - 2) |
|
|
|
|||||||||||||||||||||||||||
x®+¥
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
10.Непрерывность ф ункции в точке
Спонятием предела функции тесно связано другое важное понятие − не-
прерывность функции. Рассмотрим функцию y = f (x) , определенную в точке x0 и некоторой ее окрестности.
27
Определение 10.1. |
Функция y = f (x) |
называется непрерывной |
в точке |
|
x = x0 , |
если функция определена в точкеx = x0 и некоторой ее окрестности и |
|||
предел |
lim f (x) функции |
в точкеx0 равен |
значению f (x0 ) функции |
в этой |
|
x®x0 |
|
|
|
точке, то есть
lim f (x) = f (x0 ) .
x®x0
Это определение непрерывности функции в точке эквивалентно следующему определению.
Определение 10.2. Функция y = f (x) называется непрерывной в точке x = x0 , если функция определена в точкеx = x0 и некоторой ее окрестности и
односторонние пределы lim f (x) , lim f (x) функции в точке x0 равны между
x®x0 - x®x0 +
собой и равны значению f (x0 ) функции в этой точке, то есть выполняется равенство
lim |
f (x) = lim f (x) = f (x0 ) . |
x®x0 - |
x®x0 + |
11. Точки ра зрыва и их классификация
Точки, в которых нарушается хотя бы одно из условий непрерывности функции, называются точками разрыва этой функции.
Если x = x0 − точка разрыва функции y = f (x) , то возможны следующие случаи:
1)функция определена в окрестности точки, но неопределена в самой точке x = x0 ;
2)функция определена в точке x = x0 и ее окрестности, но не существует
предел lim f (x) функции в этой точке;
x®x0
3) функция определена в точке x = x0 и ее окрестности, существует пре-
дел lim f (x) функции в этой точке, но этот предел не равен значению f (x0 )
x®x0
функции в точке x = x0 .
Точки разрыва функции разделяются на точки разрыва первого и второго
рода.
|
Определение 11.1. Точка x = x0 называется точкой разрыва первого рода, |
если |
в этой точке существуют конечные односторонниеlim f (x) = A , |
|
x®x0 - |
lim |
f (x) = B . |
x®x0 +
При этом если:
1) односторонние пределы равны A = B , но не равны значению функции f (x0 ) в этой точке, то точка x = x0 называется точкой устранимого разрыва;
28
2) односторонние пределы не равны между собой A ¹ B , то точка x = x0 называется точкой конечного разрыва. В этом случае функции в точкеx = x0 совершает скачок на величину D | =A - B | .
Определение 11.2.Точка x = x0 называется точкой разрыва второго рода функции y = f (x) , если в этой точке хотя бы один из односторонних пределов равен бесконечности или не существует.
Пример 11.1. Исследовать на непрерывность функцию
ìsin x |
, |
x ¹ 0, |
||
ï |
|
|||
x |
||||
f (x) = í |
|
|
||
ï |
3, |
|
x = 0. |
|
î |
|
|||
Решение. Функция |
f (x) определена на всей числовой прямой. Для всех |
|||||||
x ¹ 0 функция имеет вид |
f (x) = |
sin x |
. При этом |
|
|
|
||
|
x |
|
|
|
||||
|
|
|
|
|
|
|
|
|
lim f (x) = lim |
sin x |
=1 и lim f (x) = lim |
sin x |
=1, |
||||
|
|
|||||||
x®0- |
x®0- x |
|
x®0+ |
x®0+ x |
||||
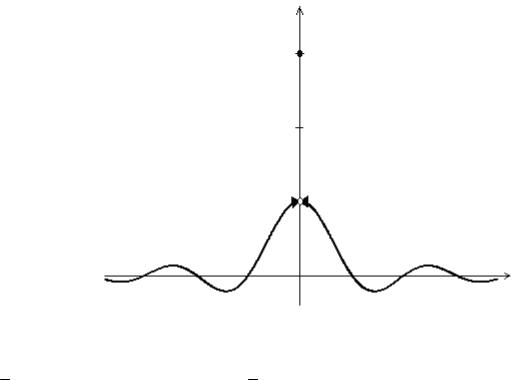
то есть односторонние пределы в точкеx = 0 существуют, конечны и равны. Однако, значение функции в точке x = 0 равно 3 . Следовательно, точка x = 0 − точка разрыва первого рода, причем, это точка устранимого разрыва. График данной функции изображен на рис. 11.1.
f (x)
3
2
1
x
-3π |
-2π -π |
0 π |
2π 3π |
Рис. 11.1. x = 0 – точка устранимого разрыва
Для устранения разрыва достаточно переопределить функцию так, чтобы
f (0) =1. Полученная функция f (x) будет непрерывной при всех x Î(-¥; + ¥).
29
Пример 11.2. Исследовать |
функцию f (x) |
на непрерывность в точках |
|
x1 = -1; x2 =0; x3 =4. |
|
|
|
|
ì(x + 2)2 - 2, |
|
x £ 0, |
f (x) = |
ï |
0 |
< x £ 4, |
ílog2 x, |
|||
|
ï |
|
x > 4. |
|
î4 - x, |
|
|
Указать характер разрыва и величину скачка в точке конечного разрыва. Построить график функции.
|
Решение. |
Функция |
f (x) |
|
определена |
и |
непрерывна |
на |
интервалах |
||||
(-¥;0] , (0;4] и (4;+¥) , где она задана непрерывными элементарными функ- |
|||||||||||||
циями. Исследуем непрерывность функции в точках x1 = -1; x2 |
=0; x3 =4. |
Най- |
|||||||||||
дем |
односторонние |
пределы |
в |
каждой |
из |
указанных |
. точкахДля точки |
||||||
x1 = -1Î(-¥;0] имеем: |
|
|
|
|
|
|
|
|
|
|
|
||
|
lim f (x) = lim ((x + 2)2 - 2)= |
-1 и lim |
f (x) = lim ((x + 2)2 - 2)= |
-1, |
|
||||||||
|
x®-1- |
x®-1- |
|
|
|
|
x®-1+ |
|
|
x®-1+ |
|
|
|
причем f (-1)= -1, то есть выполняется равенство: |
|
|
|
|
|||||||||
|
|
|
|
lim f (x) = lim= f (x) |
f (-1) . |
|
|
|
|||||
|
|
|
|
x®-1- |
|
|
x®-1+ |
|
|
|
|
|
|
|
Следовательно, в точке x1 = -1 существует предел функции, равный зна- |
||||||||||||
чению функции в этой точке. По определению это означает, что функция |
f (x) |
||||||||||||
в точке x1 = -1 непрерывна. |
|
|
|
|
|
|
|
|
|
|
|||
|
Далее вычислим односторонние пределы функции в точке x2 = 0 : |
|
|||||||||||
|
lim f (x) = lim ((x + 2)2 - 2)= |
-1 и lim f (x) ==lim log2 x |
-¥ , |
|
|||||||||
|
x®0- |
|
x®0- |
|
|
|
|
x®0+ |
x®0+ |
|
|
|
|
то |
есть предел |
функции |
справа |
|
в |
точкеx |
= 0 |
равен -¥ . По определению, |
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
x2 = 0 − точка разрыва второго рода. В этой точке функция имеет бесконечный |
|||||||||||||
разрыв. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для точки x3 = 4 получаем, что |
|
|
|
|
|
|
|
|||||
|
|
lim f (x) = lim log |
2 x = 2 и lim f (x) = lim (4 - x) = 0 , |
|
|
||||||||
|
|
x®4- |
|
x®4- |
|
|
x®4+ |
|
x®4+ |
|
|
|
|
то есть односторонние пределы в точке x3 = 4 существуют, конечны, но не рав- |
|||||||||||||
ны между собой. |
По определению, |
точка x3 = 4 − точка разрыва первого рода, |
|||||||||||
точка конечного разрыва. В этой точке функция совершает скачок на величину |
|||||||||||||
D |
|=2 - 0 | = 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
График функции |
f (x) |
изображен на рис. 11.2. |
|
|
|
|
||||||
30
