
матем 1 уск 2009
.pdfФедеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Высшая математика»
Т. В. Величко Т. В. Завьялова И. Н. Пирогова Э. Е. Поповский
МАТЕМАТИКА
Часть I
Екатеринбург
2009
3
Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Высшая математика»
Т.В. Величко Т. В. Завьялова И. Н. Пирогова Э. Е. Поповский
МАТЕМАТИКА
Часть I
Учебно-методическое пособие для студентов технических специальностей заочного отделения, обучающихся по ускоренной программе
Издание второе, исправленное и дополненное
Екатеринбург
2009
4
УДК 51
В-7
Величко Т. В., Завьялова Т. В., Пирогова И. Н., Поповский Э. Е.
Математика : учеб.-метод. пособие.–2-е изд., испр. и доп. – Екатеринбург, 2009.
– Ч. 1.– 40 с.
Пособие содержит теоретический материал и практические задания для изучения высшей математики в первом семестре, приведены некоторые математические формулы из курса элементарной математики. Предназначено для студентов технических специальностей (Э, Т, В, ПГС, СЖД, БП) с ускоренным обучением на заочном факультете.
Для успешного изучения курса высшей математики студенту заочного обучения необходимо систематическое посещение установочных занятий, самостоятельное изучение литературы по соответствующим разделам, а также выполнение всех контрольных заданий из данного пособия.
Рекомендовано к изданию на заседании кафедры «Высшая математика», протокол № 8 от 15 апреля 2009 г.
Авторы:
Т. В. Величко, ст. преподаватель кафедры «Высшая математика», УрГУПС,
Т. В. Завьялова, доцент кафедры «Высшая математика», канд. физ.-мат. наук, УрГУПС,
И. Н. Пирогова, ст. преподаватель кафедры «Высшая математика», УрГУПС,
Э. Е. Поповский, доцент кафедры «Высшая математика», УрГУПС
Рецензент:
П. С. Гончарь, доцент кафедры «Высшая математика», канд. пед. наук, УрГУПС
Учебное издание
Редактор С. В. Пилюгина
Подписано в печать 07.09.09. Формат 60 × 84 /16. Бумага офсетная. Усл. печ. л. 2,5
Тираж 250 экз. Заказ № 243
Издательство УрГУПС 620034, Екатеринбург, ул. Колмогорова, 66
© Уральский государственный университет путей сообщения (УрГУПС), 2009
5
ОГЛАВЛЕНИЕ
Введение……………………………………………………………………………...4
Краткие теоретические сведения………………………………………………...5
1.Матрицы и действия над ними…………………………………………………...5
2.Определители матриц…………………………………………………………….6
3.Решение систем алгебраических уравнений………...…………………………..7
4.Функции и их графики………………...………………………………………….8
Задания для контрольной работы № 1………………………………………...12
5.Предел и производная функции……………...…………………………………15
6.Исследование функций с помощью производной……………………………..20
7.Неопределённый интеграл………………………………………………………24
8.Определённый интеграл…………………………………………………………28
Задания для контрольной работы № 2………………………………………...33
Вопросы для подготовки к экзамену в первом семестре………………………...38
Библиографический список……………………………………………………..40
6
ВВЕДЕНИЕ
Работа студента над курсом математики на заочном факультете УрГУПС предполагает самостоятельное изучение теоретического материала и выполнение значительного числа задач и упражнений, позволяющих глубже понять содержание курса и выработать необходимые навыки в выполнении стандартных математических операций.
Пособие содержит необходимые теоретические сведения, а также некоторые примеры решения практических задач. Следует отметить, что этих сведений недостаточно не только для последующей сдачи экзамена или зачёта, но и для выполнения всех контрольных заданий.
Помимо теоретических сведений в пособие содержатся варианты заданий контрольных работ. Вариант контрольной работы студенту следует выбирать в соответствии с присвоенным шифром. А именно, последняя цифра шифра является номером варианта при выполнении контрольной работы.
При выполнении контрольных работ и представлении их на проверку студент должен руководствоваться следующими правилами.
1.Каждая контрольная должна быть выполнена в отдельной тетради и сдана в деканат или отправлена на проверку по почте в деканат заочного факультета.
2.Если при проверке контрольной работы обнаружены ошибки, то студент должен в той же тетради выполнить работу над ошибками и прислать её в деканат для повторной проверки.
3.Решение задач в контрольной работе должно быть достаточно подробным и логически последовательным. Полезно в тексте решения приводить формулировки теорем и другие теоретические сведения, на основании которых проводятся решения.
4.Для получения зачёта по контрольной работе студент должен пройти собеседование с преподавателем, где необходимо продемонстрировать понимание хода решения задач в своей контрольной работе.
7
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1. Матрицы и действия над ними
|
a |
|
a |
|
K a |
|
|
|
|
|
11 |
12 |
1m |
|
|
|
|||
Прямоугольная таблица чисел |
a |
21 |
a |
22 |
K a |
2m |
|
, содержащая |
n |
A = |
|
|
|
||||||
|
K K |
K K |
|
|
|
||||
|
|
|
an2 |
|
|
|
|
|
|
|
an1 |
K anm |
|
|
|||||
строк и m столбцов, называется матрицей размерности n ×m . Числа, содержащиеся в этой таблице, называются элементами матрицы. Матрица является квадратной, если количество строк совпадает с количеством столбцов, то есть n = m .
Две матрицы A и B называются равными, если их размерности равны и равны элементы, стоящие на соответствующих местах.
Матрицы обладают следующими свойствами:
1. Всякую матрицу A можно умножить на число λ . Результатом этого действия будет матрица, каждый элемент которой будет умножен на это число.
2. |
Суммой двух матриц A и B |
называется матрица C , такая, что |
cij = aij + bij , i =1,2,K,n, j =1,2,K,m . |
|
|
3. |
Произведением двух матриц |
A (размерность n ×m ) и B (размер- |
ность m ×k ) называется матрица C размерности n ×k , элементы которой рав-
ны cij = ai1b1 j + ai2b2 j +K+ aimbmj , |
где i =1,2,K,n, |
j =1,2,K,k . Следует от- |
|||||||||||
метить, что число столбцов матрицы A должно быть равно числу строк матри- |
|||||||||||||
цы B . |
|
|
|
|
|
|
|
|
|
−3 |
2 |
1 |
|
Пример. Пусть даны матрицы |
|
2 |
3 |
|
и |
|
|||||||
A = |
|
|
|
B = |
|
|
. Найти |
||||||
|
|
|
|
|
|
−1 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 2 4 0 |
|
||||
произведение матриц A B . |
|
|
|
|
|
|
|
|
|
||||
Решение. Пользуясь правилом умножения матриц, находим |
|
|
|
||||||||||
|
|
|
2 (−3) +3 (−2) 2 2 +3 4 |
2 |
1 +3 0 |
|
|
|
|||||
C = A B = |
|
|
|
|
|
|
|
|
= |
|
|||
|
|
|
(−1) (−3) +5 (−2) (−1) 2 +5 4 (−1) 1 +5 0 |
|
|
|
|||||||
|
|
|
|
|
|
||||||||
−12 |
16 |
2 |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
7 |
18 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Следует отметить, что произведения |
B A не существует, |
поскольку в |
||||||||||
матрице B три столбца, а в матрице A только две строки. |
|
|
|
||||||||||
Матрица, содержащая один столбец, называется вектором-столбцом, а матрица, содержащая одну строку – вектором-строкой.
8
2. Определители матриц
Каждой квадратной матрице A порядка n можно поставить в соответствие число, называемое определителем и обозначаемое A . Если матрица
размерности 2 ×2 , то её определителем является число, которое вычисляется по правилу
A |
|
= |
a11 |
a12 |
= a |
a |
22 |
− a a |
21 |
. |
(2.1) |
|
|||||||||||
|
|
|
a21 |
a22 |
11 |
|
12 |
|
|
||
|
|
|
|
|
|
|
|
|
|
Если матрица размерности 3 ×3, то её определителем является число, вычисляемое следующим образом:
a11 a12 a13
A = a21 a22 a23 = a11a22 a33 + a12 a23 a31 + a13 a21a32 − a13 a22 a31 − a11a23 a32 − a31 a32 a33
− a12 a21a33 .
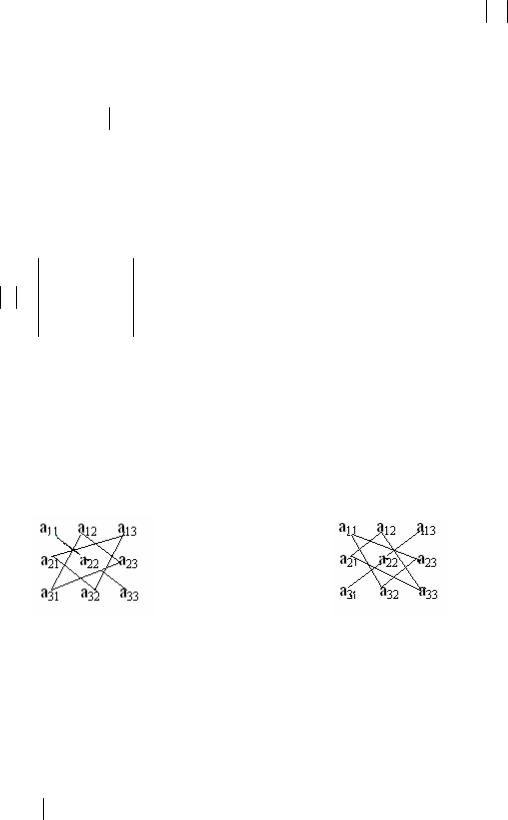
Для лучшего запоминания этой громоздкой формулы, можно использовать правило треугольников, заключающееся в следующем: сумма произведений по три элемента определителя берётся со знаком «+» и со знаком «–», согласно схемам
(2.2)
« + » |
« – » |
Здесь элементы a11, a22 , a33 называются элементами главной диагона-
ли, а элементы a13 , a22 , a31 – элементами побочной диагонали.
Другой способ вычисления определителя третьего порядка даётся формулой
|
|
|
a11 a12 a13 |
|
a22 |
a23 |
|
a21 |
a23 |
|
+ a |
|
a21 |
a22 |
|
. |
(2.3) |
|||||
|
|
|
|
|
|
|
|
|||||||||||||||
A |
|
= |
a |
|
a |
|
a |
|
= a |
− a |
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
21 |
|
22 |
|
23 |
11 |
a32 |
a33 |
12 |
a31 |
a33 |
|
13 |
|
a31 |
a32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9
3. Решение систем алгебраических уравнений
Рассмотрим систему из трёх уравнений с тремя неизвестными:
a11x + a12 y + a13 z = h1 |
|
|||||||
a21x + a22 y + a23 z = h2 |
(3.1) |
|||||||
a |
31 |
x + a |
32 |
y + a |
33 |
z |
= h |
|
|
|
|
|
3 |
|
|||
Здесь числа aij , i =1, 2,3, |
|
j =1, 2,3 |
называются коэффициентами при неиз- |
|||||
вестных, а постоянные hi , |
i =1, 2,3 называются свободными членами. |
|
||||||
Решением системы линейных уравнений (3.1) называется такая тройка чисел (x0 , y0 , z0 ) , при подстановке которой в любое уравнение системы (3.1),
получаются верные равенства.
С этой системой связаны следующие четыре определителя:
|
a11 a12 a13 |
, |
|
h1 a12 a13 |
, |
|
a11 h1 a13 |
, |
|
a11 |
a12 |
h1 |
. |
|||
= |
a21 |
a22 a23 |
x = |
h2 |
a22 a23 |
y = |
a21 |
h2 a23 |
z = |
a21 |
a22 h2 |
|||||
|
a31 |
a32 a33 |
|
|
h3 |
a32 a33 |
|
|
a31 |
h3 a33 |
|
|
a31 |
a32 |
h3 |
|
Правило Крамера. Если ≠ 0 , то система (3.1) имеет единственное решение, которое вычисляется по формулам:
x = |
x , y |
0 |
= |
y |
, z |
0 |
= z . |
(3.2) |
|
||||||||
0 |
|
|
|
|
|
|
Выписанные здесь определители вычисляются либо по правилу треугольников (2.2), либо по формуле (2.3).
Пример. Найти решение системы уравнений методом Крамера.
x |
− |
y − z |
=1 |
|
|
2 y − z |
= 0 . |
|
|
− x +3y + 2z = 7
Решение. Согласно методу Крамера нужно вычислить четыре определи-
теля:
10
|
|
1 |
|
|
|
|
|
|
−1 |
−1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
|
0 2 −1 |
|
|
|
=1 2 2 + (−1) (−1) (−1) + (−1) 0 3 − (−1) 2 (−1) − |
||||||||||||
|
|
−1 |
3 |
2 |
|
|
|
|
|
|
|
|
||||||
−1 (−1) 3 − (−1) 0 2 = 4; |
||||||||||||||||||
|
|
|
|
1 |
−1 |
−1 |
|
|
|
|
||||||||
|
|
|
||||||||||||||||
x = |
|
|
0 2 −1 |
|
=1 2 2 + 7 (−1) (−1) + (−1) 0 3 − (−1) 2 7 − |
|||||||||||||
|
|
|
|
7 |
3 |
2 |
|
|
|
|
||||||||
−1 (−1) 3 − (−1) 0 2 = 28; |
||||||||||||||||||
|
|
|
|
1 |
1 |
−1 |
|
|
||||||||||
|
|
|||||||||||||||||
y = |
|
0 |
0 −1 |
|
=1 0 2 +1 (−1) (−1) + (−1) 0 7 −(−1) 0 (−1) −1 (−1) 7 − |
|||||||||||||
|
|
|
|
|
|
|
|
−1 7 |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 0 2 = 8 |
|
|
1 |
−1 |
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||||
z = |
|
0 |
2 |
0 |
|
=1 2 7 + (−1) 0 (−1) +1 0 3 −1 2 (−1) −1 0 3 − (−1) 0 7 =16; |
||||||||||||
|
|
|
|
|
|
−1 3 |
7 |
|
|
|
|
|
|
|||||
Все определители вычислены по правилу треугольников (2.2). По формулам Крамера (3.2) имеем:
x0 = |
x = |
28 |
= 7 ; y0 = |
|
y |
= |
8 |
= 2 ; z0 = |
z = |
16 |
= 4 . |
|
4 |
|
4 |
|
4 |
||||||||
|
|
|
|
|
|
|
|
|
||||
Подставив найденные значения x0 , |
y0 , z0 |
в любое уравнение исходной систе- |
||||||||||
мы, можно убедиться, что найденное решение верно. Ответ. x0 = 7; y0 = 2; z0 = 4 .
4. Функции и их графики
Определение функции. Пусть даны два числовых множества X и Y . Если каждому элементу x из множества X ( x X ) по некоторому правилу (закону) f поставлено в соответствие вполне определённое значение y из
множества Y ( y Y ), то говорят, что на множестве X определена функция y = f (x) . Тогда X называется областью определения функции y = f (x) . Пе-
ременная x называется аргументом функции. Существует три способа задания функции:
11

1.Аналитический. Функция задается с помощью уравнения y = f (x) .
Если функция задана аналитическим выражением, то под областью определения такой функции будем понимать область значений переменной x , допустимых для этого уравнения.
2.Табличный. Функция может быть задана с помощью таблицы, содержащей значения x и y .
3.Графический. Функция задается с помощью графика. Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Пример 1. Найти область определения функции y =  x2 + 5x − 6 .
x2 + 5x − 6 .
Решение. Поскольку арифметический корень извлекается только из неотрицательных чисел, то областью определения данной функции будет множество
решений неравенства |
x2 + 5x − 6 ≥ 0 . Неравенство решается методом интерва- |
|||||||||||
лов. x2 |
+ 5x − 6 = 0 , корни этого уравнения x = −6, |
x |
2 |
=1. |
||||||||
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
-6 |
|
– |
1 |
+ |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
На рисунке область допустимых значений x заштрихована.
Ответ. x (−∞;−6] [1;+∞) .
Элементарные функции. Если в области определения функции бесконечно много значений x , то построить график такой функции весьма затруднительно. Однако существует стандартный набор основных элементарных функций, поведение которых хорошо изучено. К таким функциям относят:
– степенная |
y = xα , где α – действительное число; |
– показательная |
y = a x , где a > 0, a ≠1; |
– логарифмическая |
y = loga x , где a > 0, a ≠1; |
– тригонометрические y = cos x, y = sin x, y = tg x, y = ctg x ;
– обратные тригонометрические y = arccos x, y = arcsin x, y = arctg x, y = arcctg x .
Графики этих функций можно найти в справочнике по высшей математике [3]. Элементарными функциями будем называть также функции, которые построены из основных элементарных функций с помощью алгебраических операций и операции взятия функции от функции y = f (x) .
При построении графиков функций с помощью элементарных функций необходимо пользоваться следующими правилами преобразования графиков:
12
