ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

Кафедра «Высшая математика»

Т. В. Величко Т. В. Завьялова И. Н. Пирогова

МАТЕМАТИКА

Часть II

Екатеринбург

2010

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

Кафедра «Высшая математика»

Т. В. Величко Т. В. Завьялова И. Н. Пирогова

МАТЕМАТИКА

Часть II

Учебно-методическое пособие для студентов технических специальностей заочного отделения, обучающихся по ускоренной программе

Издание третье, исправленное и дополненное

Екатеринбург

2010

ОГЛАВЛЕНИЕ

Введение……………………………………………………………………………. 4

Дифференциальные уравнения..……………………………………………….. 5

1.Основные понятия……………………………………………………………….. 5

2.Дифференциальные уравнения первого порядка…………………………….... 6

3.Дифференциальные уравнения с разделяющимися переменными………….. 7

4.Линейные дифференциальные уравнения первого порядка…….…………... 9

5.Линейные однородные дифференциальные уравнения второго порядка

спостоянными коэффициентами ……………...………………………………… 11

6.Линейные неоднородные дифференциальные уравнения

спостоянными коэффициентами………………………………………………… 14

Ряды……………………………………………………………………………..… 16

1.Основные понятия…………………………………………………………….. . 16

2.Достаточные признаки сходимости знакоположительных рядов……............19

3.Функциональные ряды…………………………………………………………. 22

4.Применение рядов в приближённых вычислениях…………………………... 24

Задания для контрольной работы № 3………………………………………... 27

Функция двух переменных……………………………………………………... 30

1.Основные понятия……………………………………………………………… 30

2.Понятие предела функции двух переменных и частные производные…… .. 33

3.Экстремум функции двух переменных…………………………………….......36

4.Градиент функции двух переменных…………………………………………. 38

Двойной интеграл………………………………………………………………...39

1.Основные понятия……………………………………………………………. .. 39

2.Приложения двойного интеграла……………………………………………… 42

Задания для контрольной работы № 4………………………………………... 45

Вопросы к экзамену .............................................................……………………… 47 Библиографический список………………………………………………………. 48

3

ВВЕДЕНИЕ

Работа студента над курсом математики на заочном факультете УрГУПС предполагает самостоятельное изучение теоретического материала и выполнение значительного числа задач и упражнений, позволяющих глубже понять содержание курса и выработать необходимые навыки в выполнении стандартных математических операций.

Пособие содержит необходимые теоретические сведения, а также некоторые примеры решения практических задач. Однако следует отметить, что этих сведений недостаточно не только для последующей сдачи экзамена или зачёта, но и для выполнения всех контрольных заданий.

Помимо теоретических сведений в пособии содержатся варианты заданий для выполнения контрольных работ. Вариант контрольной работы студенту следует выбирать в соответствии с присвоенным шифром.

При выполнении контрольных работ и представлении их на проверку студент должен руководствоваться следующими правилами:

1.Каждая работа должна быть выполнена в отдельной тетради и сдана или отправлена на проверку по почте в деканат заочного факультета.

2.Для получения зачёта по контрольной работе студент должен пройти собеседование с преподавателем, продемонстрировав понимание хода решения задач.

3.Если при проверке контрольной работы обнаружены ошибки, то студент должен в той же тетради выполнить работу над ошибками и прислать её в деканат для повторной проверки.

4.Решение задач в контрольной работе должно быть достаточно подробным и логически последовательным. Полезно в тексте решения приводить формулировки теорем и других теоретических сведений, на основании которых делаются заключения.

4

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

1. Основные понятия

Большинство физических процессов, происходящих в природе и технике, описываются с помощью уравнений, связывающих между собой независимую переменную, искомую функцию и производную этой функции. Такие уравнения называются дифференциальными уравнениями. Далее в пособии используется сокращенная запись ДУ. Изучение ДУ началось вXVII веке и имеет большое прикладное значение и на сегодняшний день.

Решением ДУ будем называть такую функцию, зависящую от переменной x и некоторой постоянной C, которая при подстановке в уравнение обращает его в тождество.

Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком ДУ.

Пример 1. Рассмотрим простейшее ДУ первого порядкаy¢ = x . Очевидно, чтобы найти функцию y , нужно проинтегрировать обе части равенства. Реше-

Итак, получили тождественное равенство x º x . Значит, y(x) = x2 / 2 + C – верное решение исходного ДУ.

Процесс нахождения решения ДУ называетсяинтегрированием, а график решения ДУ – интегральной кривой.

Само дифференциальное уравнение задает связь между неизвестной функцией, аргументом и ее производными. Необходимо отыскать эту функцию.

Пример 2. В дифференциальном уравнении y¢¢ + y¢ - 2 y = cos x наивысший порядок производной – второй. Значит, это ДУ второго порядка. Здесь независимая переменная x , а искомая функция y(x) .

Рассмотрим задачу, составление которой приводит к ДУ.

Материальная точка массы m замедляет своё движение под действием силы сопротивления среды, пропорциональной квадрату скорости v . Найти зависимость скорости от времени. Найти скорость точки через 4 секунды после начала замедления, если известно, что v(0) =100 м/с, а v(1) = 50 м/с.

Решение. Примем за независимую переменную времяt , отсчитываемое от начала замедления движения материальной точки. Поскольку скорость зависит от времени, то v = v(t) . Для нахождения v(t) воспользуемся вторым законом Ньютона (основным законом механики): m × a = F , где a = v¢(t) – это ускорение движущегося тела, F – результирующая сила, действующая на тело в процессе движения. В условии задачи сказано, что сила сопротивления пропор-

5

циональна квадрату скорости, поэтому F = -kv2 , k – коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция v = v(t) является решением дифференциального урав-

нения m × v¢ = -k × v2 , или v¢ = - k v2 . Здесь m – масса тела. Найдя зависимость m

скорости от времени, т.е., решив полученное дифференциальное уравнение, можно определить скорость точки в любой момент времени. Решение данного

изменяется по закону v(t) = 100 . Поэтому v(4) = 20 м/с. t +1

2. Дифференциальные уравнения первого порядка

Уравнение вида F (x, y, y¢) = 0 , связывающее независимую переменную х, искомую функцию y и ее производную y¢, называется дифференциальным

уравнением первого порядка. Оно может иметь вид, разрешенный относитель-

но y¢: y¢ = f (x; y) .

Решением дифференциального уравненияпервого порядка называется всякая функция y=γ(x,C) , которая при подстановке в уравнение обращает его в тождество.

Функция у = γ(x,C) , зависящая от х и произвольной постояннойС, называется общим решением уравнения y¢ = f (x, y) в области D, если при любых допустимых значениях постояннойС функция y=γ(x,C) является решением этого уравнения и какова бы ни была точка(x0 , y0 ) Î D существует единственное значение постояннойС = С0 такое, что функция y=γ(x,C) удовлетворяет начальному условию, т. е. γ(x0 ,C0 ) = y0 . Здесь и далее D – некоторая область, состоящая из пар чисел (x; y) , при которых ДУ определено.

6

3. Дифференциальные уравнения с разделяющимися переменными

Дифференциальное уравнение первого порядкаy¢ = f (x; y) называется

дифференциальным уравнением с разделяющимися переменными, если его можно записать в виде y¢ = f1(x) × f2 ( y) .

Уравнение вида

γ1(x) × ψ1( y) =dx γ2 (x) × ψ2 ( y)dy ,

в котором функции при дифференциалах распадаются на множители, зависящие только от x и y , также является уравнением с разделяющимися переменными.

Путем деления на произведение γ2 (x) × ψ1( y) его преобразуют к уравнению с разделёнными переменными:

γ1 (x) dx = ψ2 ( y) dy .

γ2 (x) ψ1 ( y)

Общий интеграл такого уравнения имеет вид:

òγ1 (x) dx = òψ2 ( y) dy + C .

γ2 (x) ψ1 ( y)

γ2 (x) × ψ1( y) может произойти потеря частных решений, т. е. тех решений, которые обращают в нуль произведение γ2 (x) × ψ1( y) . Рассмотрим пример нахождения частного решения дифференциального уравнения.

Пример 1. Найти общее решение дифференциального уравнения первого порядка

y¢ × cos y = e2x -1 .

Решение. В этом дифференциальном уравнении производнуюy¢ запи-

шем в виде отношения дифференциалов y¢ = dy и подставим в исходное урав- dx

нение dy × cos y = e2 x -1. Умножим обе части данного равенства на dx , получим dx

cos y × dy = e2 x -1 × dx .

7

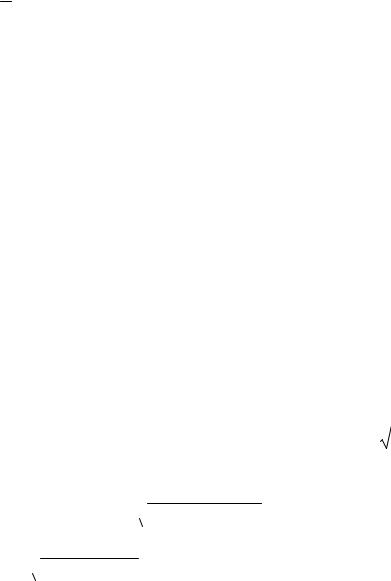
Можно заметить, что полученное уравнение – это ДУ с разделяющимися переменными. Теперь интегрируем обе части данного равенства

òcos y × dy = òe2 x -1dx .

Интеграл в левой части равенства – табличный и равен sin y , а интеграл в правой части мы найдем, пользуясь свойствами дифференциала:

y = arcsin( 1 e2 x -1 + C) – общее решение дифференциального уравнения.

2

Пример 2. Найти частное решение уравнения

левой части полученного равенства оставляем все множители, зависящие от y ,

а в правой части собираем множители, зависящие от x . Получим следующее равенство:

общее решение исходного ДУ. Чтобы найти частное решение ДУ, необходимо подставить начальное условие y(0) =1 в общее решение ДУ. Итак, подставим

y =1, x = 0 . Получим 1 = ±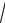4ln(0 +1) + 2C Þ C = 0,5 . Полученное значение постоянной C = 0,5 нужно подставить в общее решение ДУ.

Имеем, y = ±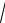4ln(x +1) +1 – частное решение ДУ при заданном начальном условии y(0) =1.

8

4. Линейные дифференциальные уравнения первого порядка

Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции, и её производной и не включающее их произведение. Оно имеет вид:

где p(x) и g(x) – функции, зависящие от x и непрерывные в той области, в которой требуется проинтегрировать уравнение (4.1).

Если g (x) = 0 , то уравнение (4.1) называется линейным однородным. Оно является уравнением с разделяющимися переменными и имеет общее -ре шение

y(x) = C ×e-ò p( x)dx .

Если в уравнении (4.1) g (x) ¹ 0, p(x) ¹ 0 , то общее решение уравнения (4.1) ищется в виде произведения двух других функций, т. е. с помощью подстановки y = u(x) × v(x) . Тогда y¢ = u¢× v + v¢ ×u . Подставляя выражения y и y¢ в исходное уравнение (4.1), получаем:

Одну из этих функций можно выбирать. Подберём функцию v = v(x) так, чтобы выражение в скобках было равно нулю, т. е. решим дифференциальное уравнение с разделяющимися переменными:

v¢ + p(x) × v = 0,

отсюда найдем v = v(x) ,

имеем dv = - p(x) × dx – это ДУ с разделяющимися переменными. v

Интегрируя обе части, получим:

ln v = -ò p(x) × dx + ln C = γ(x) + ln c ,

где γ(x) какая-либо первообразная для - p(x) .

Еще раз воспользуемся свободой выбора и примем C = 1. Тогда v = eγ ( x ) или v = eγ ( x) .

9