
математика ч 2
.pdf
212. |
y¢ = xy 2 + 2 , |
y(0) = 2 . |
217. |
y¢ = ye x +1, |
y(0) = 2 . |
213. |
y¢ = e x + xy , |
y(0) = 1. |
218. |
y¢ = y 2 + x3 , |
y(0) = 1. |
214. |
y¢ = y 2 + x2 , |
y(0) = 1. |
219. |
y¢ = xy + y 2 , |
y(0) = 1. |
215. |
y¢ = e2 x + x2 y , |
y(0) = 1. |
220. |
y¢ = e3 x + x - y 2 , |
y(0) = 2 . |
ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
1. Основные понятия
Переменная z называется функцией двух переменных x и y, если каждой упорядоченной паре чисел (x; y) из некоторого множества парD по определенному правилу поставлено в соответствие единственное значение переменной z. При этом переменные x и y называются независимыми переменными (или аргументами), а переменная z – функцией. Обозначение функциональной зависимости между x, y и z имеет вид: z = f (x; y) . Множество D = D( f ) всех пар
(x, y) называется областью определения функции двух переменных, а множе-
ство значений, принимаемых z в области определения, называется множест-
вом значений функции.
Графиком функции двух переменных называется множество точек пространства, координаты которых имеют вид (x; y; f (x, y)), где (x, y) Î D( f ) .
Впрямоугольной декартовой системе координатOxyz графиком является
вобщем случае поверхность.
Некоторые примеры поверхностей.
1. Плоскость, задается уравнением Ax + By + Cz + D = 0 , где A, B, C, D – некоторые числа (рис. 1).
Рис. 1
30

2. Параболоид. Уравнение параболоида имеет вид z = (x - x0 )2 + ( y - y0 )2 , где (x0 ; y0 ; z0 ) – координаты вершины. График параболоида (рис. 2) имеет вид:
Рис. 2
3. Цилиндрическая поверхность описывается уравнением F (x; y) = 0 , т. е.
не содержит переменную z . Например, x2 + y 2 = 4 – цилиндр (рис. 3).
Поскольку графиком функции x2 + y 2 = 4 является окружность с центром в точке (0; 0) и радиусом R = 2 , то в плоскости Oxy рисуем эту окружность. Учитывая, что мы имеем дело с фигурой в пространстве, то в данном случае получается, что какое бы мы значение для z ни взяли, у нас получаются окружности.
Рис. 3
31

|
|
Пример. Найти область D определения функции |
|||||||||||||||||
|
|
|
|
|
1 |
|
|
. Построить область D . |
|||||||||||
z = |
|
9 - x2 - y2 |
+ |
|
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||||
|
y - x2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Решение. Функция z |
|
|
определена при |
||||||||||||||
|
ì |
- x |
2 |
- y |
2 |
³ 0; |
|
ì |
|
|
2 |
+ y |
2 |
£ 9; |
|||||
D : |
ï9 |
|
|
|
Û |
ïx |
|
|
|||||||||||
í |
|
|
2 |
|
|
|
|
í |
|
|
|
|
2 |
|
|
|
|||
|
ï |
|
|
> 0 |
|
|
|
|
ï |
|
|
|
|
. |
|
||||
|
îy - x |
|
|
|
|
|
îy > x |
|
|
||||||||||
Строим границы этой области. |
|
|
|
|
|||||||||||||||
|
|
Уравнением x2 + y 2 = 9 описывается окружность с центром в начале ко- |
|||||||||||||||||
ординат и радиусом 3; уравнение |
y = x2 задает параболу с вершиной в начале |
||||||||||||||||||
координат. Парабола нарисована пунктиром, поскольку точки, лежащие на параболе, не удовлетворяют неравенству y > x2 , так как неравенство строгое (рис. 4). Чтобы определить, какую часть плоскости заштриховать, необходимо взять координаты любой точки, не лежащей на границе, подставить в исходное неравенство. Если получено верное неравенство, то штрихуется та часть плоскости, в которой находилась произвольная точка. Если при подстановке получено неверное неравенство, то штрихуется та часть плоскости, которая лежит по другую сторону от границы. Область D заштрихована (рис. 4).
Рис. 4
32
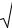
2.Понятие предела функции двух переменных
ичастные производные
|
Для функции двух переменных введем понятие предела. |
|
|||||||
|
Окрестностью точки P0 (x0 ; y0 ) называется внутренность |
круга с цен- |
|||||||
тром в этой точке. |
|
|
|
|
|
||||
|
Число А называется пределом функции z = f (x; y) = f (P) при P ® P0 , ес- |
||||||||
ли для любого положительного числаe > 0 |
найдется такая малая |
окрестность |
|||||||
точки P0 (x0 ; y0 ) , что для любой точки P (x |
; y ) |
из этой окрестности(за ис- |
|||||||
ключением, |
может |
быть, точки |
P0 (x0 ; y0 ) ) |
выполняется |
неравенство |
||||
|
f (P) - A |
|
< e . При этом пишут: lim |
f (P) = A или |
lim f (x, y) = A . |
||||
|
|
||||||||
|
|
|
|
|
P®P0 |
|
|
x®x0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
y®y0 |
|
|
Разность |
f (x0 + Dx; y0 ) - f (x0 ; y0 ) = Dx z называется частным прираще- |
|||||||
нием по х функции z = f (x; y) в точке P0 (x0 ; y0 ) . Аналогично определяется
частное приращение по y: D y z = f (x0 ; y0 + Dy) - f (x0 ; y0 ) .
Предел отношения частного приращения функции к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю, называет-
ся частной производной функцииz = f (x; y) по данному аргументу
|
¶z |
|
|
|
Dx z |
|
¶z |
|
D y z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= |
lim |
|
, |
|
= lim |
|
|
. Используются также обозначения z¢x , z¢y , fx¢, f y¢ . |
||||||||||||||||||||||
|
¶x |
|
Dx®0 Dx ¶y |
Dy®0 Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Полным |
приращение |
функции z = f (x; y) |
|
в точке M (x0 , y0 ) |
называется |
|||||||||||||||||||||||||
разность Dz = f (x0 + Dx; y0 + Dy) - f (x0 ; y0 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Функция |
z = f (x; y) называется |
|
дифференцируемой |
в |
точкеP (x |
0 |
; y |
0 |
) , |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||
если |
ее |
полное |
приращение |
в этой |
|
точке |
может |
быть |
представлено |
в виде |
||||||||||||||||||||||
Dz = ADx + BDy + a(Dx, Dy), |
где |
А и В – |
|
не зависят от ∆х и ∆у, а |
α(∆х,∆у) |
– |
||||||||||||||||||||||||||
бесконечно малая, для которой |
lim |
|
a(Dx, Dy) |
|
= 0 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Dx®0, |
|
Dx |
2 |
+ Dy |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Dy®0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Главная, линейная относительно ∆х и ∆у, часть приращения функции назы- |
||||||||||||||||||||||||||||||
вается |
полным |
дифференциалом |
|
|
этой |
функции |
и |
обозначаетсяdz: |
||||||||||||||||||||||||
dz = ADx + BDy . Можно доказать, что dz |
= |
¶z |
dx |
+ |
|
¶z |
dy . |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Рассмотрим примеры. |
|
|
|
|
|
|
|
|
¶x |
|
|
¶y |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Пример |
1. |
Найти |
|
частные |
|
производныеz¢x |
и |
z¢y |
для |
функции |
|||||||||||||||||||
|
z = ln(x - y 2 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
33

Решение. Чтобы найти z¢x , зафиксируем переменную y (мысленно при-
дадим ей значение, например, |
y = 3). |
Тогда |
|
|
|
|
|
|
|
|
|
|||||||||
z¢x = (ln( x - y2 ))x¢ = |
1 |
|
× (x - y |
2 )¢x = |
1 |
|
(1 - 0) |
= |
|
1 |
|
. |
|
|
||||||
|
x - y2 |
x - y2 |
x - y2 |
|
|
|||||||||||||||
Для нахождения z¢y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
зафиксируем переменную x . Имеем: |
|
|
|
|
||||||||||||||||
z¢y = (ln( x - y2 )) ¢ |
= |
1 |
|
× (x - y2 )¢y = |
|
1 |
|
× (0 - 2 y) = |
|
|
1 |
|
|
× (-2 y) . |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y |
|
x - y2 |
|
|
|
|
|
x - y2 |
|
|
|
|
x - y2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример 2. |
|
|
Найти |
частные |
производныеz¢x |
|
|
и z¢y |
для функции |
|||||||||||
z = x × sin( x + y) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Пусть y = const , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
z¢x = (x ×sin(x + y))¢x |
=(производная= |
произведения) |
x¢×sin(x + y) + |
|||||||||||||||||
+ x × (sin(x + y))¢x |
= 1×sin(x + y) + x × cos(x + y) ×(x + y)¢x |
= |
|
|
|
|
||||||||||||||
= sin( x + y) + x × cos(x + y)(1 + 0) = sin( x + y) + x × cos(x + y) . |
|
|
|
|
||||||||||||||||
Пусть x = const , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z¢y = (x ×sin(x + y))¢y |
|
(постоянную |
x |
вынесем за знак производной= ) |
||||||||||||||||
= x × (sin(x + y))¢y = x × cos(x + y) × (x + y)¢y = xcos(x + y) × (0 +1) = x × cos(x + y).
Частными производными второго порядка называются частные произ-
водные, взятые по соответствующей переменной от первой производной. На-
пример, вторая частная производная по переменной x от функции z = f (x; y)
равна z¢xx¢ = (z¢x ¢)x . Смешанной частной производной второгопорядка назы-
вается производная от функции z = f (x; y) взятая, сначала по одной перемен-
ной, потом по другой переменной. Причем справедливо равенство |
¢¢ |
|
|
¢¢ |
||||||||||||||||||||||
zxy |
= z yx . |
|||||||||||||||||||||||||
|
Пример 3. Найти |
|
частные |
|
|
|
|
|
|
|
¢¢ |
¢¢ |
¢¢ |
для |
функции |
|||||||||||
|
|
|
производные zxx |
, z yy |
и zxy |
|||||||||||||||||||||
z = xy + ln(x - y) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Решение. |
Первая производная по x равна |
z¢x = (y= |
const= ) |
y + |
|
1 |
|
, |
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x - y |
|||
z¢¢ = |
(=y= |
const ) |
( y + |
= 1 |
|
)¢ |
0 - |
= |
1 |
|
- |
|
1 |
. |
|
|
|
|
|
|
||||||
|
|
|
(x - y)2 |
|
|
|
|
|
|
|||||||||||||||||
xx |
|
|
|
|
|
x - y x |
|
(x - y)2 |
|
|
|
1 |
|
|
|
|
|
|
||||||||
Первая производная по y равна z¢y |
= (x= |
const= ) |
x - |
, |
|
|
|
|
|
|||||||||||||||||
x - y |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда |
¢¢ |
|
(x |
|
|
|
|
|
-1× (-1) |
|
|
|
-1 |
|
. |
|
|
|
|
|
|
|
|
|
||
= |
|
= |
|
- |
= |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
zyy |
|
const ) |
0 |
|
|
(x |
- y)2 |
|
|
(x - y)2 |
|
|
|
|
|
|
|
|
|
|
|||||
34
¢¢ |
|
¢ ¢ |
( y + |
1 |
¢ |
1 |
. |
|||
|
|
|
||||||||
Найдем смешанную производную zxy |
= (zx ) y = |
x - y |
) y =1 + |
(x - y)2 |
||||||
|
|
|
|
|
|
|
|
|
||
Если функция двух переменных z = f (x, y) задана неявно |
|
|
||||||||
F (x; y; z) = 0 , |
|
|
|
|
|
|
|
|||
то ее частные производные по переменным x, |
y находятся по формулам: |
|||||||||
|
F ¢ |
|
|
Fy¢ |
|
|
|
|
||
z¢x = - |
x |
; |
z¢y = - |
|
. |
|
|
|
||
|
|
|
|
|
||||||
|
Fz¢ |
|
|
Fz¢ |
|
|
|
|
||
Формула для вычисления полногодифференциала функции двух пере-
менных имеет вид
dz = z¢x × dx + z¢y × dy , |
(2.1) |
или
dz = d x z + d y z .
Здесь d x z – частный дифференциал функции по переменной x .
Одним из геометрических приложений частных производных функции
трех переменных является понятие касательной плоскости и нормальной пря-
мой к поверхности в некоторой |
точке. Пусть поверхность задана уравнением |
F (x; y; z) = 0 , функция F (x; y; z) |
дифференцируема по всем переменным. То- |
гда в точке M (x0 ; y0 ; z0 ) , принадлежащей данной поверхности, можно провес-
ти касательную плоскость. Прямая, перпендикулярная касательной плоскости,
называется нормальной прямой или нормалью.
|
Уравнение касательной плоскости к поверхности F (x; y; z) = 0 в точке |
|||||||||
M (x0 |
; y0 ; z0 ) имеет вид |
|
|
|
|
|
|
|
|
|
|
Fx¢(x0 ; y0 ) × (x - x0 ) + Fy¢(x0 ; y0 ) × ( y - y0 ) + Fz¢(x0 ; y0 ) × (z - z0 ) = 0 . |
(2.2) |
||||||||
|
Уравнения нормальной |
прямой к |
поверхностиF (x; y; z) = 0 в |
точке |
||||||
M (x0 |
; y0 ; z0 ) имеют вид |
|
|
|
|
|
|
|
|
|
|
|
x - x0 |
|
= |
y - y0 |
|
= |
z - z0 |
. |
(2.3) |
|
|
|
|
|
|
|
||||
|
|
Fx¢(x0 ; y0 ) |
Fy¢(x0 ; y0 ) |
Fz¢(x0 ; y0 ) |
|
|||||
35
Пример. Найти уравнение касательной плоскости и уравнения нормали к поверхности z 2 - x2 - y = 4 в точке (0;0;-2) .
Представим уравнение поверхности в виде F (x; y; z) = 0 . Имеем
F (x; y; z) = z2 - x2 - y - 4 .
Найдем частные производные функции F (x; y; z) в точке (0;0;-2) :
Fx¢ = -2 × x , Fx¢(0;0;-2) = -2 ×0 = 0;
Fy¢ = -1, Fy¢(0;0;-2) = -1;
Fz¢ = 2 × z , Fz¢(0;0;-2) = 2 ×(-2) = -4 .
Подставим в уравнения (2.2), (2.3), получим
0 × (x - 0) + 0 × ( y - 0) - 4 × (z + 2) = 0, - 4 × z - 8 = 0 или z + 2 = 0 – уравнение
касательной плоскости к данной поверхности в точке (0;0;-2) ;
x - 0 |
= |
y - 0 |
= |
z + 2 |
– уравнения нормальной прямой. |
0 |
|
|
|||
0 |
- 4 |
|
|||
3. Экстремум функции двух переменных
Точка P0 (x0 ; y0 ) |
называется точкой |
локального |
максимума |
|
функции |
||||||||
z = f (x; y) , а |
значение функции в ней z0 = f (x0 ; y0 ) – максимумом, |
если су- |
|||||||||||
ществует такая окрестность этой точки, что для всех точек P0 (x0 ; y0 ) |
из этой |
||||||||||||
окрестности, |
отличных |
от P0 (x0 ; y0 ) , |
выполняется |
неравенство |
|||||||||
f (x, y) < f (x0 , y0 ) . |
называется точкой |
локального |
минимума |
|
функции |
||||||||
Точка |
P0 (x0 ; y0 ) |
|
|||||||||||
z = f (x; y) , |
а |
значение функции в ней z0 = f (x0 ; y0 ) – минимумом, |
если су- |
||||||||||
ществует такая окрестность этой точки, что для всех точек P (x ; y |
) |
из этой |
|||||||||||
окрестности, |
отличных |
от P0 (x0 ; y0 ) , |
выполняется |
неравенство |
|||||||||
f (x, y) > f (x0 , y0 ) . |
|
|
|
|
|
¶f |
|
|
|
¶f |
|
||
Точка, в которой обе частные производные равны нулю, т. е. |
= 0, |
|
|
= 0 , |
|||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
¶x |
|
|
¶y |
||
называется стационарной точкой функции z = f (x; y) .
Экстремум функции z = f (x, y) находят, пользуясь следующими правилами:
36
1.Функция z = f (x, y) должна быть дифференцируема по перемен-
ным x, y .
2.Находим точку M (x0 ; y0 ) (точки) возможного экстремума, решая
ìz¢x |
= 0 |
систему двух уравнений: í |
. Иными словами, ищем стацио- |
îz¢y |
= 0 |
нарные точки.
3.Находим значения вторых частных производных в точке возможно-
го экстремума M (x0 ; y0 ) :
A = |
¢¢ |
(x0 ; y0 ), |
B = |
¢¢ |
(x0 ; y0 ), |
C = |
¢¢ |
(x0 ; y0 ) . |
f xx |
f xy |
f yy |
||||||
4. Составим определитель |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
D = |
A |
|
B |
= AC - B2 . |
|
|
|
|
|
|
|
|
B |
|
C |
|
|
|
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
если D > 0 , |
то функция z = f (x, y) в точке M (x0 ; y0 ) имеет |
|||||
|
|
экстремум, причем при А < 0 – максимум, при А > 0 – минимум; |
|||||||||
|
|
|
|
б) если D < 0 , |
то функция z = f (x, y) в точке M (x0 ; y0 ) экс- |
||||||
|
|
тремума не имеет; |
|
|
|
|
|
|
|||
|
|
|
|
в) |
если D = 0 , то в точке M (x0 ; y0 ) экстремум может быть, а |
||||||
|
|
может не быть. Необходимы дополнительные исследования. |
|||||||||
|
Пример. |
|
Найти экстремумы функции z = x3 + y3 - 3xy . |
||||||||
Находим частные производные данной функции: |
|||||||||||
|
|
|
|
|
z¢x = 3x2 - 3y, z¢y = 3y2 - 3x . |
||||||
Найдем стационарные точки. Получим |
|
|
|
||||||||
|
¢ |
ì |
2 |
- |
3y = 0; |
|
|
|
|
|
|
ìz x = 0; |
ï3x |
|
|
(0;0) и M |
|
(1;1) . |
|||||
í |
z¢y = 0 |
Û í |
2 |
|
Þ M |
1 |
2 |
||||
î |
ï |
- 3x = 0 |
|
|
|
|
|||||
|
3y |
|
|
|
|
|
|
|
|||
|
|
î |
|
|
|
|
|
|
|
|
|
Найдем вторые частные производные исследуемой функции:
37
¢¢ |
= (3x |
2 |
¢ |
¢¢ |
= (3y |
2 |
¢ |
¢¢ |
= (3x |
2 |
¢ |
= -3 . |
zxx |
|
- 3y)x |
= 6x, z yy |
|
- 3x) y |
= 6 y, zxy |
|
- 3y) y |
Проведем исследования сначала для точки M1 (0;0) .
Значения вторых частных производных в этой точке равны
¢¢ |
(M |
1 ) = 6 × 0 = 0, |
¢¢ |
(M1 ) = -3, |
¢¢ |
(M1 ) = 6 × 0 |
= 0 . |
|||||||||
A = zxx |
B = zxy |
|
|
C = z yy |
||||||||||||
Составим |
определитель D = |
|
A |
B |
|
= |
|
0 |
- 3 |
|
= -9 . Так как D < 0 , то в точке |
|||||
|
|
|
|
|||||||||||||
|
|
|
|
|
B |
C |
|
|
|
- 3 |
|
0 |
|
|
|
|
M1 (0;0) данная функция экстремума не имеет.
Исследуем точку M 2 (1;1) . Подставим координаты этой точки во вторые
частные производные:
¢¢ |
(M 2 ) |
= 6 ×1 = 6, |
¢¢ |
|
¢¢ |
||||||||
A = zxx |
B = zxy (M 2 ) = -3, |
C = z yy (M 2 ) = 6 ×1 = 6 . |
|||||||||||
Тогда D = |
|
A |
B |
|
= |
|
6 |
- 3 |
|
= 27 . Поскольку D = 27 > 0 и A = 6 > 0 , то функция |
|||
|
|
|
|
||||||||||
|
|
|
B |
C |
|
|
|
- 3 |
6 |
|
|
|
|
имеет |
в точке M 2 (1;1) локальный |
минимум. Подставим координаты точки |
|||||||||||
M 2 (1;1) в выражение функции zmin = z(M 2 ) =13 +13 - 3 ×1×1 = -1.
4. Градиент функции двух переменных
Вектор, координатами которого являются значения частных производных
функций U (x, y, z) в точке |
M (x, y, z) , называется градиентом функции U и |
|||||||
uuuuuur |
ì |
¶U |
|
¶U |
|
¶U |
ü |
|
обозначается gradU = í |
; |
; |
ý. |
|||||
|
¶y |
¶z |
||||||
|
î |
¶x |
|
þ |
||||
Градиентом функции z = f (x, y) в точке M (x0 ; y0 ) называется вектор, координаты которого равны значениям частных производныхz = f (x, y) , вы-
численных в рассматриваемой точке M (x0 ; y0 ) : |
|
|
uuuuuuur |
r |
r |
grad(z) = z¢x (M 0 ) ×i + z¢y (M 0 ) × j
Этот вектор указывает направление и величину наибольшей скорости возрастания функции z = f (x, y) в точке M (x0 ; y0 ) . Величина скорости равна:
38

|
|
uuuuuuur |
|
|
|
|
|
|
|
|
|
|
(z¢x (M 0 )2 + (z¢y (M 0 ))2 . |
||||
|
|
grad(z) |
= |
|
||||
Пример. |
Для функции z = xy 2 - 2x найти градиент в точке M (1;2) . |
|||||||
Решение. |
Найдем частные производной данной функции |
|||||||
|
|
|
z¢x = (xy2 - 2x)¢x = y2 - 2 , |
|||||
|
|
|
z¢y = (xy2 - 2x)¢y = 2xy . |
|||||
Вычислим значения частных производных в точке M : |
||||||||
|
z¢x (M ) = 22 - 2 = 2 , |
z¢y (M ) = 2 ×1× 2 = 4 . |
||||||
Согласно формуле градиент данной функции в точке M равен |
||||||||
|
uuuuuuur |
|
r |
|
r |
uuuuuuur |
||
|
grad(z) = 2 ×i |
+ 4 × j |
или grad(z) ={2;4}. |
|||||
|
|
ДВОЙНОЙ ИНТЕГРАЛ |
|
|
||
|
|
1. |
Основные понятия |
|
|
|
Пусть в |
областиD |
плоскости Oxy задана |
непрерывная |
функция |
||
z = f (x; y) . Разобьем |
область D на n малых |
площадок Dsi (рис. 1), |
причем |
|||
n |
|
|
|
|
|
|
åDsi равна площади |
области D. В каждой |
площадке |
выберем произвольную |
|||
i =1 |
и найдем значение функции z в ней: zi = f (xi ; yi ) . |
|
||||
точку Pi (xi ; yi ) |
|
|||||
|
|
|
|
n |
|
|
Составим |
интегральную сумму вида å f (xi ; yi )Dsi . Если существует |
|||||
|
|
|
|
i =1 |
|
|
предел этой суммы при условии, что каждая из элементарных площадок стягивается в точку и он не зависит ни от способа разбиения областиD на элементарные области, ни от способа выбора в них точкиPi (xi ; yi ) , то этот предел на-
зывается двойным интегралом от функции f (x, y) по области D и обознача-
ется òò f (x, y)ds .
D
n
Таким образом, òò f (x, y)ds = lim å f (xi ; yi )Dsi . |
|
D |
n®¥ i =1 |
39
