
матан
.pdf
Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения
Н. В. Медведева П. П. Скачков
ВВЕДЕНИЕ В АНАЛИЗ
Типовой расчет
Екатеринбург
2010
Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Высшая математика»
Н. В. Медведева П. П. Скачков
ВВЕДЕНИЕ В АНАЛИЗ
Типовой расчет
Учебно-методическое пособие для студентов всех специальностей
Екатеринбург
2010
2
УДК 517.1 М 42
Медведева, Н. В.
М 42 Введение в анализ. Типовой расчет : учеб.-метод. пособие для студентов всех специальностей / Н. В. Медведева, П. П. Скачков. − Екатеринбург:
УрГУПС, 2010.− 64 с.
Пособие предназначено для выполнения индивидуальных заданий типового расчета по теме «Введение в анализ» студентами всех специальностей дневной формы обучения.
Первая часть пособия содержит краткие теоретические сведения, необходимые для решения задач типового расчета. Рассмотрены примеры для всех типов заданий. Приведены подробные решения наиболее важных из них с пояснениями и ссылками на теоретический материал.
Во второй части представлены индивидуальные задания. По уровню сложности и тематике они носят характер, соответствующий требованиям программы по математике для технических вузов.
УДК 517.1
Пособие рекомендовано к изданию на заседании кафедры «Высшая математика», протокол № 8 от 21.04. 2010 г.
Авторы: Н. В. Медведева, ст. преподаватель кафедры «Высшая математика», канд. физ.-мат. наук, УрГУПС;
П. П. Скачков, доцент кафедры «Высшая математика», канд. физ.-мат. наук, УрГУПС
Рецензенты: Э. Е. Поповский, доцент кафедры «Высшая математика», УрГУПС;
В. Л. Розенберг, старший научный сотрудник ИММ УрО РАН, канд. физ.-мат. наук
3
ÓУральский государственный университет путей сообщения (УрГУПС), 2010
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ................................................................... |
4 |
|
ФУНКЦИЯ ..................................................................................................... |
4 |
|
1. |
Понятие функции одной переменной. График функции. Способы зада- |
|
|
ния функции ............................................................................................... |
4 |
2. |
Основные свойства функции ..................................................................... |
5 |
3. |
Обратная и сложная функции.................................................................... |
6 |
4. |
Основные элементарные функции и их графики ..................................... |
7 |
5. |
Построение графиков функций с помощью преобразований ................ |
12 |
ПРЕДЕЛ ФУНКЦИИ ................................................................................... |
15 |
|
6. |
Предел функции в точке и на бесконечности ......................................... |
15 |
7. |
Односторонние пределы .......................................................................... |
18 |
8. |
Бесконечно большие и бесконечно малые функции .............................. |
20 |
9. |
Основные теоремы о пределах ................................................................ |
22 |
НЕПРЕРЫВНОСТЬ ФУНКЦИИ ................................................................. |
26 |
|
10. Непрерывность функции в точке........................................................... |
26 |
|
11. Точки разрыва и их классификация ...................................................... |
27 |
|
12. Непрерывность функции в интервале и на отрезке. Основные теоре- |
||
|
мы о непрерывных функциях ................................................................ |
30 |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ......................................................... |
31 |
|
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ.............................................................................. |
32 |
|
3
4

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
ФУНКЦИЯ 1. Понятие функции одной переме нной. График функции.
Способы задания ф ункций
Одним из основных математических понятий является понятие функции. Определение 1.1. Переменная величина y называется функцией пере-
менной величины x , если каждому значению x , взятому из некоторого множества, по определенному правилу(закону) f ставится в соответствие единственное значение y .
При этом x называют независимой переменной или аргументом, y −
зависимой переменной (функцией). Функциональную зависимость y от x в общем виде обозначают y = f (x) .
Определение 1.2. Множество значений x , для которых определяются значения функции y в силу правила f (x) , называется областью определения функции y = f (x) и обозначается D( f ) .
Определение 1.3. Множество значений, принимаемых переменной y по правилу f (x) , называется областью значений функции y = f (x) и обозначается E( f ) .
Определение 1.4. Графиком функции y = f (x) называется множество всех точек координатной плоскости Oxy , абсциссы которых равны допустимым значениям аргумента x , а ординаты – соответствующим значениям функции y , т.е. точек M (x, f (x)), где x Î D( f ).
Существует несколько способов задания функции:
1)аналитический (представлено аналитическое выражение y = f (x) );
2)табличный (представлена таблица, содержащая значения x и соответствующие им значения y );
3)графический (представлен график функции).
Если функция задана аналитически, то ее область определения и множество значений находятся из анализа заданного выражения.
Пример 1.1. Найти область определения функции y = lg(x2 - 4) + 
 x + 3 .
x + 3 .
Решение. Так как логарифмическая функция определена при x2 - 4 > 0 , а подкоренное выражение приx + 3 ³ 0 , то областью определения исходной функции будут решения системы двух неравенств:
ìx2 - 4 > 0 |
Û |
ì(x - 2)(x + 2) > 0 |
||
D( y) : í |
+ 3 ³ 0 |
í |
x ³ -3. |
|
î x |
|
î |
||
5
Первое неравенство можно решить методом интервалов:
 x
x
Откуда
ìéx > 2,
D( y) : ïíêëx < -2, Þ - 3 £ x < -2, x > 2. ïî x ³ -3.
Таким образом, область определения данной функции имеет вид
D( y) :[-3;-2) È (2;+¥).
Пример 1.2. Найти множество значений функции y = sin x - 4.
Решение. Зная, что функция y = sin x принимает все значения от -1 до 1, то с помощью преобразования неравенств получим
-5 £ sin x - 4 £ -3.
Значит, функция y = sin x - 4 может принимать все значения из отрезка [-5; -3]
и множество значений функции имеет вид
E( y) :[-5;-3].
2. Основные свойства ф ункций
Пусть функция y = f (x) определена на множестве D : D( f ) .
Определение 2.1. Функция y = f (x) |
называется четной (нечетной), ес- |
|
ли для любого значения аргумента x |
из множества D значение аргумента -x |
|
также принадлежит множествуD |
и |
выполняется равенствоf (-x) = f (x) |
( f (-x=) - f (x) ). |
|
|
График четной функции симметричен относительно оси Oy , а нечетной – относительно начала координат.
Определение 2.2. Функция y = f (x) называется возрастающей (убывающей) на множестве D , если для любых значений аргументов x1, x2 , принад-
лежащих |
множеству D , из |
неравенства x1 < x2 |
следует |
неравенство |
f (x1 ) < f (x2 ) ( f (x1 ) > f (x2 ) ). |
y = f (x) называется неубывающей (невоз- |
|||
Определение 2.3. Функция |
||||
растающей) на множестве D , если для любых значений аргументовx1, x2 , принадлежащих множеству D , из неравенства x1 < x2 следует неравенство
f (x1 ) £ f (x2 ) ( f (x1 ) ³ f (x2 ) ).
Возрастающие, невозрастающие, убывающие, неубывающие функции на множестве D называются монотонными на этом множестве, а возрастающие и убывающие – строго монотонными. Интервалы, на которых функция моно-
тонна, называются интервалами монотонности.
6
Определение 2.4. Функция y = f (x) называется ограниченной на множестве D , если существует такое положительное число M , что для всех значений аргумента x из множества D выполняется неравенство | f (x) | £ M .
Из определения следует, что график ограниченной функции лежит между прямыми y = -M и y = M .
Определение 2.5. Функция y = f (x) называется периодической на множестве D , если существует такое положительное число T , что для любого x из множества D значение (x ± T ) также принадлежит множеству D и выполняется равенство f (x ± T ) = f (x) .
Такое число T называется периодом функции. Тогда, если T − период функции, то числа n ×T , где n = ±1; ± 2;.... также будут периодами этой функции. Обычно наименьшее положительное число T , удовлетворяющее равенству f (x + T ) = f (x) , называют основным периодом функции.
3. Обратная и сложная функция
Рассмотрим функцию y = f (x) с областью определения D : D( f ) и множеством значений E : E( f ) .
Определение 3.1. Если каждому значению y из множества E соответствует единственное значение x из множества D , то функция x = φ ( y) называется обратной к функции y = f (x) . Обозначают x = φ ( y) = f -1 ( y) .
Для обратной функции y − независимая переменная или аргумент, а x − зависимая переменная (функция).
Функции y = f (x) и x = f -1 ( y) являются взаимно обратными функциями.
Например, функции y = 2x и x = log2 y являются взаимно обратными.
Из определения следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает(убывает), то обратная ей функция также возрастает (убывает).
Для того чтобы найти функцию x = φ ( y) , обратную к функции y = f (x) ,
достаточно |
решить уравнение f (x) = y относительно x |
(если это возможно). |
При этом x |
и y меняются ролями. Если независимую переменную вновь обо- |
|
значить буквой x , а зависимую переменную обозначить |
y , то обратная функ- |
|
ция запишется как y =φ (x) . |
|
|
График обратной функцииy = φ(x) получается |
из графика исходной |
|
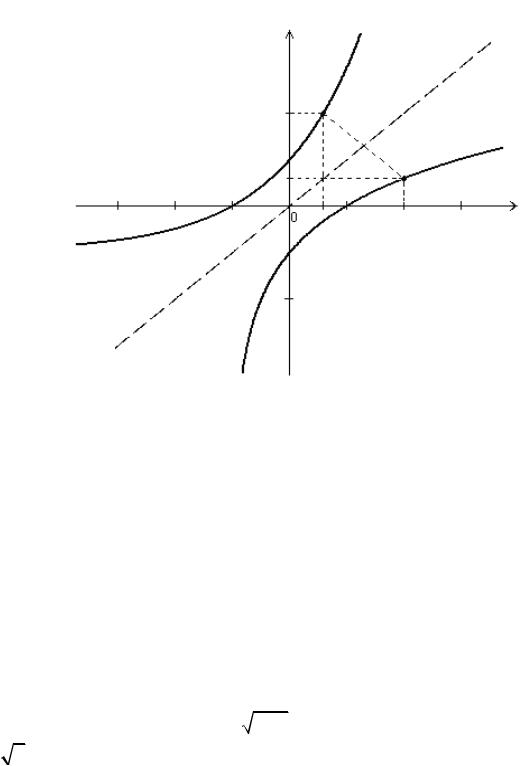
функции с помощью зеркального отражения последнего относительно биссектрисы первой и третьей координатных четвертей. Действительно, из рис. 3.1 видно, что точка M1 ( x0 ; y0 ) кривой y = f (x) становится точкой M 2 ( y0 ; x0 ) кри-
вой x = φ ( y) . Точки M1 и M 2 симметричны относительно прямой y = x .
7
y |
|
y = f (x) |
|
|
y = x |
y0 |
M1 |
y = φ(x) |
|
|
M2
x0 |
|
x |
|
x0 |
|
|
y0 |
|
|
|
Рис. 3.1. Графики взаимно обратных функций
Определение 3.2. Пусть функция y = f (u) определена на множестве U , а переменная u , в свою очередь, является функцией u = g (x) , определенной на множестве X , причем для любого x из X соответствующее значение u = g (x) принадлежит множеству U . Тогда говорят, что на множестве X определена функция
y = f (g(x)) ,
которая называется сложной функцией от x (или суперпозицией, композици-
ей функций f и g ).
Переменную u = g (x) называют промежуточным аргументом.
Например, функция y = cos3x есть композиция двух функций y = cosu и u = 3x .
Сложная функция может иметь несколько промежуточных аргументов.
Например, функция y = sin 
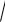 e2 x+3 есть композиция функций y = sin u , u =
e2 x+3 есть композиция функций y = sin u , u = 
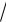 v , v = ew и w = 2x + 3.
v , v = ew и w = 2x + 3.
4. Основные элементарные функции и их граф ики
Определение 4.1. Основными элементарными функциями называются следующие функции:
1)степенная функция y = xα , α − действительное число;
2)показательная функция y = ax , где a > 0, a ¹ 1;
8
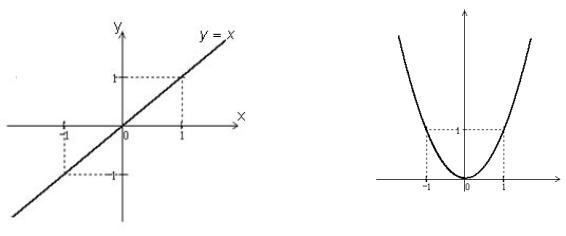
3)логарифмическая функция y = loga x , где a > 0, a ¹ 1;
4)тригонометрические функции:
y = cos x , y = sin x , y = tg x , y = ctg x ;
5) обратные тригонометрические функции:
y = arccos x , y = arcsin x , y = arctg x , y = arcctg x .
Рассмотрим области определения, множества значений и графики основных элементарных функций.
Степенная функция y = xα .
1)α − целое положительное число. В этом случае функция определена на всей числовой оси, то есть D( y) : (-¥;+¥) .
2)α − целое отрицательное число. В этом случае функция определена при всех x , не равных нулю, то есть D( y) : (-¥;0) È (0;+¥) .
При этом, если α |
− нечетное число, то множество значений функции |
|||
имеет вид E( y) : (-¥; +¥) , если α − четное число, то E( y) :[0; +¥) . |
||||
3) |
α − положительное рациональное число, α = |
p |
. Если q − четное чис- |
|
|
||||
|
|
|
q |
|
ло, то |
функция будет |
определена при всех неотрицательныхx , то есть |
||
D( y) :[0;+¥) . Если q − нечетное число, то функция определена для любых x ,
то есть D( y) : (-¥;+¥) . Множество значений функции в этом случае может быть E( y) :[0; +¥) или E( y) : (-¥;0], или E( y) : (-¥; +¥) (см. рис. 4.1).
Графики степенных функций при некоторых значенияхα , представлены на рис. 4.1.
α =1 |
α = 2 |
|
y |
y = x2
x
9
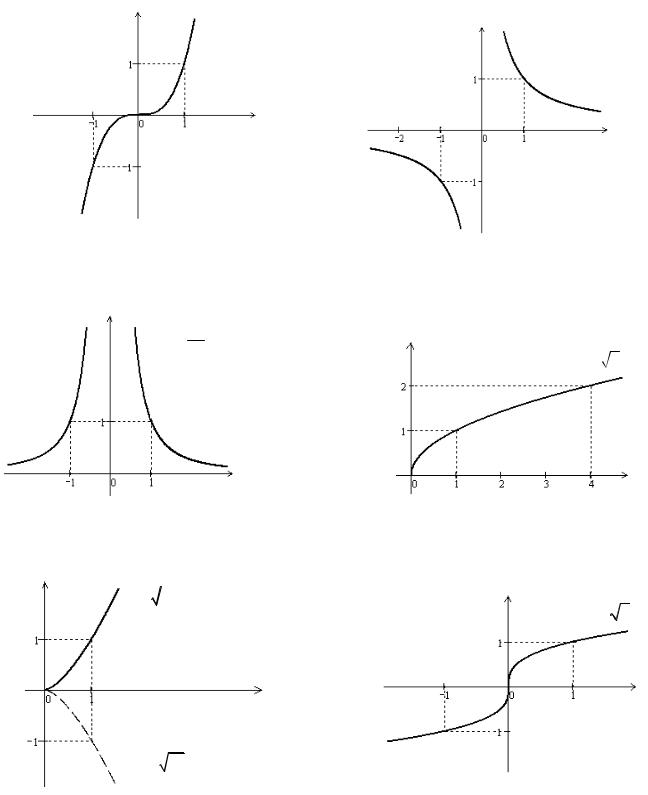
α = 3 |
α = -1 |
|
y |
y |
|
y = x3 |
1 |
|
|
y = |
|
|
x |
|
|
|
|
|
x |
|
x
α = -2 |
1 |
|
α = |
||
2 |
||
|
y |
1 |
|
|
y = |
y |
||
x2 |
y = 
 x
x
x x
α = |
3 |
|
|
α = |
1 |
|
|
|
|
|
|
||||||||
2 |
|
|
3 |
|
|
|
|||
y |
|
|
y |
|
|
||||
|
|
|
|||||||
y = x3 |
|
|
|||||||
|
|
|
|
|
|
|
y = 3 x |
||
|
|
|
|
x |
|
|
|
|
x |
y = -
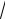 x3
x3
Рис. 4.1. Графики степенных функций
Показательная функция y = ax , где a > 0, a ¹ 1.
10
