
матан
.pdf
Функция определена на всей числовой оси, то есть D( y) : (-¥;+¥) . Множество значений функции имеет вид E( y) : (0;+¥) .
Графики |
показательной |
функции |
при0 < a <1 и a >1 представлены на |
рис. 4.2. |
|
|
|
Логарифмическая функция y = loga x , где a > 0, a ¹ 1. |
|||
Функция |
определена |
при всех |
положительных значенияхx , то есть |
D( y) : (0; +¥) . Множество значений функции имеет вид E( y) : (-¥; +¥) . |
|||
Графики логарифмической функции при 0 < a <1 и a >1 представлены на |
|||
рис. 4.3. |
|
|
|
|
a >1 |
|
0 < a <1 |
y |
y = ax |
y |
|
|
y = ax |
||
a
a
x |
x |
|
Рис. 4.2. Графики показательной функции
a >1 |
0 < a <1 |
y |
y |
y = loga x |
|
|
y = loga x |
|
x |
|
a |
x |
|
a |
||
|
Рис. 4.3. Графики логарифмической функции
Тригонометрические функции y = cos x , y = sin x , y = tg x , y = ctg x .
11

Функции y = cos x и y = sin x определены на всей числовой оси, то есть D( y) : (-¥;+¥) . Множество значений данных функций– это отрезок [-1;1], то есть E( y) :[-1;1] .
Функции y = tg x и y = ctg x определены при всех значениях x , кроме точек соответственно
x ¹ p + pk, k ÎZ и x ¹ pn, n ÎZ.
2
Множество значений данных функций имеет вид E( y) : (-¥; +¥) . Графики тригонометрических функций изображены на рис. 4.4.
y |
y = cos x |
y |
y = sin x |
|
|||
|
|
|
-3π -2π -π 0 π 2π 3π |
x |
|
x |
|
-3π -2π -π |
0 π 2π |
|||
3π |
y |
y = tg x |
y |
y = ctg x |
|
|
-π |
|
|
0 |
|
π |
|
x |
-2π |
|
3π |
- |
π 0 |
π |
π 3π 2π |
||||
- |
3π |
- |
π |
π |
3π |
- |
2 |
|
2 |
|
2 |
|
2 |
|
||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 4.4. Графики тригонометрических функций
Обратные тригонометрические функции y = arccos x , y = arcsin x , y = arctg x , y = arcctg x .
Функции y = arccos x и y = arcsin x определены на отрезке [-1;1], то есть D( y) :[-1;1] . На рис. 4.5 жирно выделены графики главных ветвей y = arccos x и
y = arcsin x , |
значения |
|
|
которых |
заполняют |
соответственно |
промежутки |
||
E( y) :[0;p ] |
и E( y) : |
é |
p |
; |
p |
ù |
|
|
|
ê- |
|
|
ú . |
|
|
|
|||
2 |
2 |
|
|
|
|||||
|
|
ë |
|
û |
|
|
|
||
12
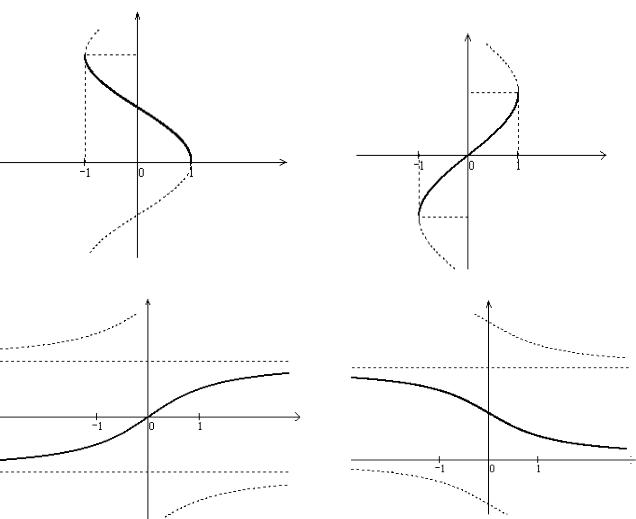
Функции y = arctg x |
и y = arcctg x определены при всех значенияхx , то |
есть D( y) : (-¥;+¥) . На |
рис. 4.5 жирно выделены графикиглавных ветвей |
y = arctg x и y = arcctg x , |
значения которых заполняют соответственно проме- |
æ |
|
p |
|
p |
ö |
|
|
|
||
жутки E( y) : ç |
- |
|
|
|
; |
|
÷ |
и E( y) : (0;p ) . |
|
|
2 |
|
2 |
|
|
||||||
è |
|
|
|
ø |
|
|
|
|||
|
|
y |
|
|
|
y = arccos x |
y |
|
||
|
|
π |
|
|
|
y = arcsin x |
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
π |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
2 |
|
|
|
|
x |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
- |
π |
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
y |
y = arctg x |
|
|
y |
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
y = arcctg x |
|
π |
|
|
|
|
π |
||
2 |
|
|
|
|
||||
|
|
|
|
|
|
|||
|
|
|
x |
|
|
|
π |
|
|
|
|
|
2 |
|
|||
- |
π |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
||
Рис. 4.5. Графики обратных тригонометрических функций
Определение 4.2. Элементарной называется функция, которую можно задать одним аналитическим выражением, составленным из основных элементарных функций с помощью конечного числа арифметических действий и конечного числа операций взятия функции от функции.
5. Построение графиков ф ункции с помощью преобразований
При построении графиков функций с помощью основных элементарных функций можно пользоваться следующими правилами преобразования графи-
ков:
13
1) график функции y = f (x) + a |
получается из графика функцииy = f (x) |
||||||||
путем его сдвига вдоль оси Oy на a единиц вверх при a > 0 , или на | a | |
единиц |
||||||||
вниз при a < 0 ; |
|
|
|
|
|
|
|
|
|
2) график функции y = f (x + a) |
получается из графика функцииy = f (x) |
||||||||
путем его сдвига вдоль оси Ox на a единиц влево при a > 0 , или на | a | |
единиц |
||||||||
вправо при a < 0 ; |
|
|
|
|
|
|
|
|
|
3) график функции y = A × f (x) |
получается из графика функции y = f (x) |
пу- |
|||||||
тем его растяжения вдоль оси Oy в |
A раз при A >1, или сжатия в |
1 |
|
|
раз при |
||||
|
A |
||||||||
0 < A <1; |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
4) график функции y = f (k × x) |
получается из графика функции y = f (x) |
пу- |
|||||||
тем его сжатия вдоль осиOx в k |
раз при k >1, или растяжения в |
1 |
|
раз при |
|||||
k |
|||||||||
0 < k <1; |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
5) график функции y = - f (x) получается из графика функции y = f (x) |
пу- |
||||||||
тем его симметричного отражения относительно оси Ox ; |
|
|
|||||||
6) график функции y = f (-x) получается из графика функции y = f (x) |
пу- |
||||||||
тем его симметричного отражения относительно оси Oy ;
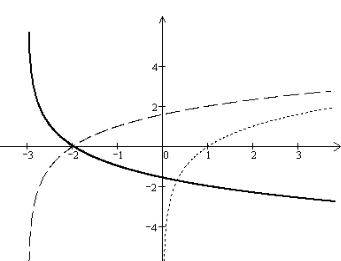
Пример 5.1. С помощью преобразования графиков элементарных функций построить график функции y = -log2 (x + 3) .
Решение. Сначала построим график элементарной логарифмической
функции |
y1 = log2 x . График функции y2 = log2 (x + 3) получаем путём сдвига |
||||
графика |
функции y1 по |
осиOx |
на 3 единицы |
влево. |
График функции |
y3 = -log2 (x + 3) получаем |
из графика функцииy2 |
путём |
его симметричного |
||
отражения относительно оси Oy. |
Графики данных функций изображены на |
||||
рис. 5.1. |
|
|
|
|
|
y
y3 = -log3 (x + 3)
x
y2 = log3 (x + 3) |
y1 = log3 x |
Рис. 5.1. Построение графика функции y = -log2 (x + 3)
14
Графическое изображение функций дает возможность находить приближенное решение любого уравнения с одним неизвестным.
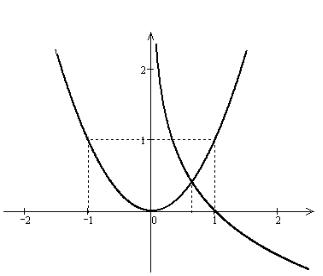
Пример 5.2. Решить уравнение приближенно графическим методом x2 + log3 x = 0 .
Решение. Данное уравнение запишем в виде x2 = -log3 x .
y
y1 = x2
А
x
x
y2 = -log3 x
Рис. 5.2. Графики функций y1 = x2 и y2 = -log3 x
Для того, чтобы найти корни уравнения, (если они есть) построим графики функций y1 = x2 и y2 = -log3 x . Из рис. 5.2 видно, что графики данных функций имеют одну общую точкуА. Абсцисса x точки А и будет являться корнем исходного уравнения. По построению находим приближенное значение x » 0, 64 .
Пример 5.3. Дана функция f (x) =| x +1| + | 2x - 4 | -9 . |
Записать в виде со- |
||
ставной функции и построить ее график. Решить уравнение |
f (x) = 0. |
||
Решение. По определению |
ìa, если a ³ 0; |
|
|
|
|
|
|
|
| a | = í |
|
|
|
|
î-a, если a < 0. |
|
Обозначим g1 (x) = x +1 и g2 (x) = 2x - 4 . Рассмотрим промежутки, на ко- |
|||
торых функции g1 (x) и g2 (x) |
принимают положительные и отрицательные |
||
значения. Для этого решим уравнения g1 (x) = 0 и g2 (x) = 0 : |
|
||
|
x +1 = 0 и 2x - 4 = 0 ; тогда x1 = -1 и x2 = 2 . |
||
Определим знаки |
функций g1 (x) |
и g2 (x) на промежутках (-¥; -1] , (-1;2] и |
|
(2;¥) : |
(-¥; -1] |
(-1;2] |
(2;¥) |
x |
|||
g1 (x) = x +1 |
- |
+ |
+ |
g2 (x) = 2x - 4 |
- |
- |
+ |
15
Следовательно, при x £ -1 функция f (x) имеет вид
f (x) = -(x +1) - (2x - 4) - 9= -x -1 - 2x + 4 - 9= -3x - 6 .
При -1 < x £ 2 :
f (x) = (x +1) - (2x - 4) - 9= x +1 - 2x + 4 - 9= -x - 4 ,
и x > 2 :
f (x) = (x +1) + (2x - 4) - 9 = x +1 + 2x - 4 - 9 = 3x -12 .
Таким образом, f (x) можно записать в виде составной функции:
ì-3x - 6, |
x £ -1; |
|
ï |
- 4, |
-1 < x £ 2; |
f (x) = í-x |
||
ï |
-12, |
x > 2. |
î3x |
||
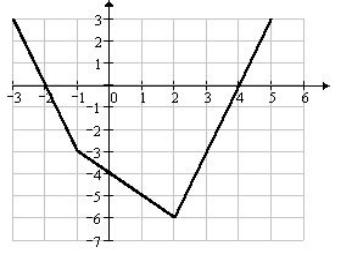
График данной функции изображен на рис. 5.3.
y
x
Рис. 5.3. График функции f (x)
Из рис. 5.3 видно, что решениями уравнения f (x) = 0 являются x1 = -2 и x2 = 4 . Действительно, если x £ -1, то функция f (x) = -3x - 6 принимает значение, равное нулю при x = -2 Î(-¥;-1]. На промежутке -1 < x £ 2 функция имеет вид f (x) = -x - 4 и -x - 4 = 0 при x = -4 Ï(-1;2]. При x > 2 имеем f (x) = 3x -12 и 3x -12 = 0 при x = 4 Î(2;+¥) .
ПРЕДЕЛ ФУНКЦИИ
6. Предел функции в точке и на бесконечности
Пусть x0 − произвольная точка на числовой прямой.
Определение 6.1. δ −окрестностью точки x0 называется интервал
(x0 - δ; x0 + δ) , где δ > 0 .
16
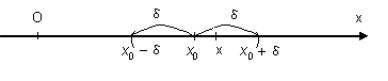
Число x0 называется центром окрестности, а число δ − ее радиусом.
Рис 6.1. δ -окрестность точки x0
Если x принадлежит интервалу (x0 - δ; x0 + δ) , то выполняется неравенство x0 - δ < x < x0 + δ или | x0 - x |< δ . Выполнение последнего неравенства означает попадание точки x в δ -окрестность точки x0 (см. рис. 6.1).
Пусть функция y = f (x) определена в некоторой окрестности точкиx0 , кроме, может быть, самой точки x0 .
Определение 6.2. Число A называется пределом функции y = f (x) в
точке x = x0 (или при x ® x0 ), если для любого положительного числа ε существует положительное число δ = δ(ε) такое, что для всех x , удовлетворяющих
неравенству | x - x |< δ |
и |
отличных |
xот, |
выполняется |
неравенство |
0 |
|
|
0 |
|
|
| f (x) - A |< ε. Тогда кратко пишут |
|
|
|
|
|
|
|
lim f (x) = A. |
|
|
|
|
|
x®x0 |
|
|
|
Другими словами, |
если значения функции f (x) неограниченно прибли- |
||||
жаются к некоторому |
числуA , |
когда значения |
аргумента x |
неограниченно |
|
приближаются к x0 , при этом x ¹ x0 , то число A называется пределом функции при стремлении x к x0 .
Используя логические символы "– означающего «для любого», «для всякого»; $– «существует», «найдется», определение 6.2 формально записывается следующим образом:
("ε > 0 $δ δ(ε) >=0 "x ¹ x0 :| x - x0 |< δ Þ | f (x) - A |< ε) Û lim |
f (x) = A. |
x®x0 |
|
Следовательно, lim f (x) = A тогда и только тогда, когда |
для любой ε − |
x®x0 |
|
окрестности точки A найдется такая δ − окрестность точки x0 , что для любого |
|
x ¹ x0 из этой δ − окрестности соответствующее значение функции f (x) попадает в ε − окрестность точки A .
Геометрический смысл предела lim f (x) = A заключается в том, что гра-
|
x®x0 |
фик функции y = f (x) |
расположен между прямыми y = A + ε и y = A - ε для |
всех x , принадлежащих |
δ − окрестности точки x0 (см. рис. 6.2). |
17

y
y = f (x)
A + ε |
|
y = A + ε |
|
|
|
f (x) |
|
y = A |
A |
|
|
|
|
|
A - ε |
|
|
|
|
y = A - ε |
O |
|
x |
x0 - δ |
x0 |
x x0 + δ |
Рис. 6.2. Геометрический смысл предела lim f (x) = A
x®x0
Например, если f (x) = x2 +1, то при приближении x к 2 значения функции
приближаются к 22 +1 = 5 , то есть предел данной функции при x ® 2 равен 5 : lim (x2 +1) = 5.
x®2 |
вычислить предел функцииf (x) |
|
В этом случае для того чтобы |
при |
|
x ® x0 , нужно найти значение функции f (x) в точке x = x0 . |
|
|
Пусть функция y = f (x) определена на промежутке (-¥; +¥) . |
|
|
Определение 6.3. Число A называется пределом функции y = f (x) |
при |
|
x ® ¥ , если для любого положительного |
числаε существует положительное |
|
число M = M (ε) такое, что для всех x , удовлетворяющих неравенству | x | > M , выполняется неравенство | f (x) - A |< ε. Такой предельный переход обозначают
lim f (x) = A.
x®¥
|
Если x |
принимает только |
положительные |
значения, то |
пишут x ® +¥ , |
если |
только |
отрицательные, то |
x ® -¥ и |
соответственно обозначают |
|
lim |
f (x) = A и lim f (x) = A. |
|
|
|
|
x®+¥ |
|
x®-¥ |
|
|
|
|
Другими словами, если значения функции f (x) неограниченно прибли- |
||||
жаются к некоторому числуA , когда значения |
аргумента x |
неограниченно |
|||
возрастают (убывают), то есть при x ® +¥ ( x ® -¥ ), то число A называется пределом функции при x ® +¥ ( x ® -¥ ).
Формально определение 6.3 записывается следующим образом:
("ε > 0 $M = M (ε) > 0 "x :| x | > M Þ | f (x) - A |< ε) Û lim=f (x) A.
x®¥
18

Следовательно, lim f (x) = A тогда и только |
тогда, когда для любой ε − |
|
|
x®¥ |
|
окрестности точки A найдется такое положительное числоM = M (ε) > 0 , что |
||
для любого x |
из интервала (-¥; M ) или (M ;+¥) |
соответствующее значение |
функции f (x) |
попадает в ε − окрестность точки A . |
|
y
y = f (x)
A + ε
f (x1)
A
f (x2 )
y = A - ε |
A - ε |
x2 -M О |
M x |
|
1 |
y = A + ε
y = A
x
Рис. 6.3. Геометрический смысл предела lim f (x) = A
x®¥
График функции y = f (x) в этом случае расположен между прямыми y = A + ε и y = A - ε для любого x из интервала (-¥; M ) или (M ;+¥) (см. рис.
6.3). В этом состоит геометрический смысл предела lim f (x) = A.
x®¥
7. Односторонние пределы ф ункции
Способ приближения x к точке x0 существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.
Определение 7.1. Число B1 называется пределом функции y = f (x) сле-
ва в точке x = x0 , если для любого положительного числа e существует положительное число δ = δ(ε) такое, что для всех x из интервала (x0 - δ; x0 ) , выполняется неравенство | f (x) - B1 |< ε.
Обозначают lim f (x) = B1.
x®x0 -
Другими словами, если значения функции f (x) неограниченно приближаются к некоторому числуB1 при x ® x0 таким образом, что x принимает
19
значения строго меньшие, чем x0 , то число B1 |
называется пределом функции |
||||||||
слева. |
|
|
|
|
|
|
|
|
|
Формально определение 7.1 записывается следующим образом: |
|
|
|||||||
("ε > 0 $δ |
δ(ε) >=0 "x Î(x0 - δ; x0 ) Þ | f (x) - B1 |
|< ε) Û lim f (x) = B1. |
|
||||||
|
|
|
|
|
|
|
x®x0 |
|
|
Аналогично вводится понятие предела функции справа, который обозна- |
|||||||||
чается lim |
f (x) = B2 : |
|
|
|
|
|
|
|
|
x®x0 + |
|
|
|
|
|
|
|
|
|
("ε > 0 $δ |
δ(ε) > 0="x Î(x0 ; x0 + δ) Þ | f (x) - B2 |
|< ε) Û lim f (x) = B2. |
|
||||||
|
|
|
|
|
|
|
x®x0 + |
|
|
Пределы слева и справа называются односторонними пределами. |
|
|
|||||||
Если |
существуют оба |
односторонних |
предела |
функции и |
они |
равны |
|||
B = B1 = B2 , |
то говорят, что существует предел lim f (x) = B функции |
f (x) |
в |
||||||
точке x = x0 . |
|
|
|
x®x0 |
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
||
Если |
B1 ¹ B2 , то предел lim f (x) = B |
функции |
в точке x = x0 |
не су- |
|||||
ществует. |
|
|
x®x0 |
|
|
|
|
|
|
|
|
f (x) = x2 +1 |
|
|
|
|
|
|
|
Например, |
для функции |
левый |
и правый пределы |
в точке |
|||||
x0 = 2 существуют и равны соответственно |
|
|
|
|
|
|
|||
|
|
lim (x2 +1) = 5, |
lim (x2 +1) = 5. |
|
|
|
|||
|
|
x®2- |
|
x®2+ |
|
|
|
|
|
y
x
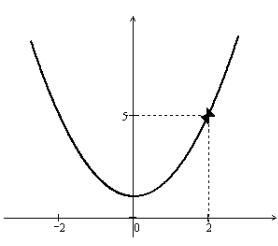
Рис. 7.1. График функции f (x) = x2 +1
Значения односторонних пределов данной функции в точкеx0 = 2 изображены на рис. 7.1. Следовательно, так как односторонние пределы функции f (x) = x2 +1 в точке x0 = 2 имеют одинаковые значения, то существует предел
функции f (x) в точке x0 = 2 и lim(x2 +1) = 5.
x®2
20
