Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

математика ч 2

.pdf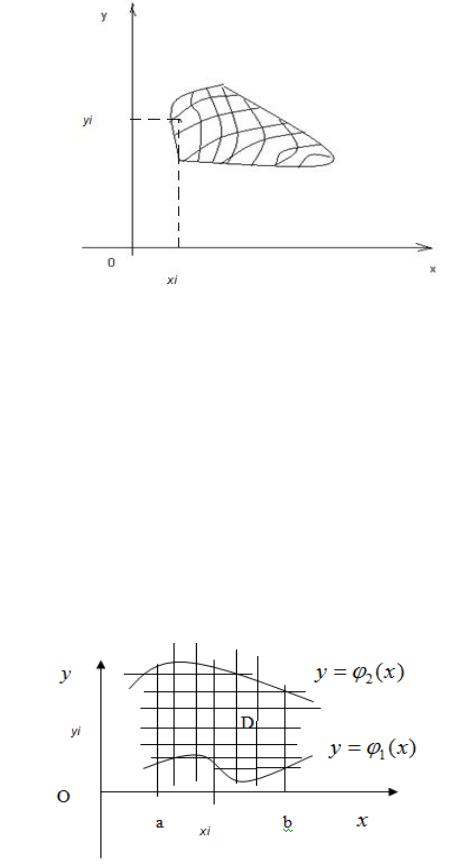

Скачиваний:

Добавлен:

17.05.2015

Размер:

457.66 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 55

Рис. 1

В этом случае функцияz = f (x, y) называется интегрируемой в об-

ласти D ;

область D называется областью интегрирования; переменные x, y – переменными интегрирования.

Двойной интеграл вычисляется сведением к последовательному вычислению двух определенных интегралов.

Пусть область D ограничена прямыми x = a, x = b и линиями, причем j2 (x) ³ j1 (x) . Тогда область называется правильной в направлении оси Oy .

В этом случае каждая прямая, параллельная оси Oy , пересекает границу области не более чем в двух точках. Разобьем область прямыми, параллельными осям координат.

Разбивая область D прямыми x = xi и y = yi , получим, что область D состоит из множества частичек (рис. 2), площадь которых равна dS = dx × dy .

Рис. 2 Составляя интегральную сумму, получим

	b	j2 ( x)
òò f (x; y)dxdy = ò dx		ò f (x; y)dy .	(1.1)
D	a	j1 ( x)

j2 ( x)

Здесь, при вычислении внутреннего интеграла ò f (x; y)dy , переменная x счи-

тается постоянной.			j1 ( x )

Если область интегрирования D является правильной в направлении оси
Ox , т. е. ограничена прямыми y = c,	y = d и кривыми x = g1 ( y),			x = g2 ( y) ,
g 2 (x) ³ g1 (x) , то двойной интеграл вычисляется по формуле
	d	g 2 ( y)
òò f (x; y)dxdy = òdy		ò f (x; y)dx .		(1.2)
D	c	g1 ( y)
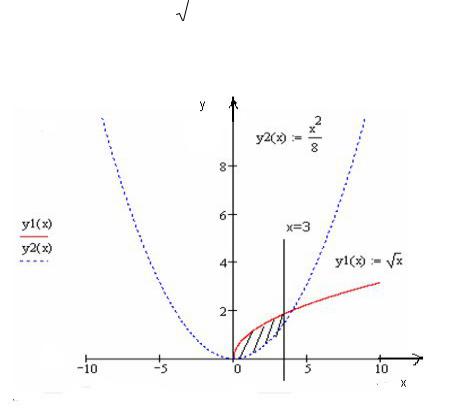
Пример. Вычислить двойной интеграл òò x × y 2dxdy , если область D огра-
			D
		x2
ничена линиями x = 0, x = 3, y = x,	y =
			.
		8
Решение. Строим область D (рис. 3).

Рис. 3

Заштрихованная область D правильная в направлении оси Oy .

																						3								æ					3			æ		2	ö3 ö
					3				x						3						y	3			x		3			æ	(		x)		3		1	æ	x	2	ö3 ö
òò x × y2 dxdy = ò dx								ò			x × y 2dy			= ò dx (x ×							y		)		2		= ò			x × ç	(		x)			-	1	×ç	x		÷	÷dx =
òò x × y2 dxdy = ò dx								ò			x × y 2dy			= ò dx (x ×									)	x	2	8	= ò			x × ç						-		×ç			÷	÷dx =
D					0		x	2		8					0						3			x		8	0			ç		3					3	ç	8		÷	÷
D					0		x			8					0						3						0			è		3					3	è	8		ø	ø
		3æ		x7		ö						æ	2x7 / 2			x8		ö	3											è								è			ø	ø
	1									1											221184								- 45927

																												3
=		òç x5 / 2	-			÷dx =						ç		-				÷	0	=														» 3,92.
=		òç x5 / 2	-		3	÷dx =						ç		-			4	÷		=														» 3,92.
	3	ç		8	3	÷				3		ç	7		8		4	÷								86016
	3	0è		8		ø				3		è	7		8			ø								86016

2. Приложения двойного интеграла

Площадь плоской фигуры. Рассмотрим фигуру D на плоскости, ограниченную графиками функций y =j1(x) , y = j2 (x) , причем j1(x) £ j2 (x) , x = a, y = b . Тогда площадь полученной фигуры можно вычислить с помощью двойного интеграла:

	b	j2 ( x )
S = òò dxdy = ò dx		ò dy .	(2.1)
D	a	j1 ( x )
Пример 1. Найти площадь фигуры,		ограниченной линиями	y = sin x ,

x = p2 , y = 0 . Сделать чертеж.

Решение. Строим область, ограниченную данными линиями. На рис. 4 область заштрихуем.

Рис. 4

Найдем координаты точек пересечения линий: A(0;0), B(π2;0), C(π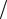2;1) . Область интегрирования является правильной в направлении оси Ox . Тогда согласно (2.1) площадь фигуры равна

			p 2	sin x	p 2	p 2	p0	2 =
S = òòdxdy = òdx òdy = ò (sin x - 0)dx = òsin xdx = -cos x							p0	2 =
D	0			0	0	0
= -(cos		p	- cos 0) = -(0 -1) = 1 кв. ед.
= -(cos			- cos 0) = -(0 -1) = 1 кв. ед.
	2
	Объем			цилиндрического		тела. Рассмотрим		тело, ограниченное

сверху поверхностью z = f (x, y) ³ 0 , снизу – замкнутое областью D , с боков цилиндрической поверхностью, перпендикулярной плоскости xOy . Такое тело называется цилиндрическим. Найдем объем этого тела. Разобьем область D произвольным образом на n областей Di , площади которых равны DSi . Рассмотрим полученные цилиндрические столбики, у которых в основании область Di , а сверху кусок поверхности z = f (x, y) . Обозначим объем такого цилиндрического тела Vi . Очевидно, что в своей совокупности они составляют

объем всего цилиндрического тела: V = å Vi . Объем части данного тела при-

					i=1
ближенно		равен	произведению		площади		основания			на , высоту. е.
Vi	» f (xi ; yi ) × DSi , где (xi ; yi ) – произвольная точка, рассмотренная в области
Di	с площадью DSi .
	Тогда объем всего цилиндрического тела равен сумме объемов всех -ма
					n	n
леньких цилиндрических столбиков V = å Vi						» å f (xi ; yi ) × DSi .
					i=1	i=1
	Равенство будет более точным, если количество разбиений области D на
кусочки Di		будет увеличиваться. Предположим,					что	количество			разбиений
увеличивается n ® ¥ , а				каждая Di	стягивается в			точку,	тогда объем
	n
V = lim å f (xi ; yi ) × DSi , или по определению равен двойному интегралу:
	n®¥
	maxdi ®0 i=1
				V = òò f (x; y)dxdy .							(2.2)
				D
( di – «диаметр» области Di ).
	Пример 2. Найти объем тела, ограниченного поверхностями x2 + y2 = 8 ,
x = 0 , y = 0 , z = 0 , x + y + z = 4 .
	Решение. Графиком			x2 + y2 = 8 ,	z Î R	является цилиндр. При z = 0 по-
лучается окружность с центром в точке(0;0)						и радиусом R = 2				.	Графиком
лучается окружность с центром в точке(0;0)						и радиусом R = 2			2	.	Графиком
x + y + z = 4		является плоскость. Найдем точки пересечения цилиндра и плос-
кости, решив систему уравнений:

ìx2 + y2 = 8;

íx + y + z = 4;

ïîz = 0.

Данная система имеет единственное решение: M (2;2;0) . Строим тело, ограниченное этими поверхностями.

	Рис. 5
Область D – это четверть круга:	x2 + y 2 = 8 , где 0 £ x £ 2 2 . Для удобства

и наглядности построим область интегрирования отдельно.

Рис. 6

Найдем объем тела.

					2				8- x 2								2									2
					2		2		8- x 2								2		2						y	2			8 - x	2
V = òò f (x; y)dxdy =						òdx			ò(4 - x - y)dy =									òdx(4 y - xy -							y		)				=
V = òò f (x; y)dxdy =						òdx			ò(4 - x - y)dy =									òdx(4 y - xy -									)	0			=
		D			0				0									0						2				0
	2										- x2
		2								8						æ				æ x			ö					æ				x öö
																																		2	2
			(4 8 - x2 - x		8 - x2																													2	2
= ò									-				)dx = ç16arcsinç										÷	+ 8sin(2arcsinç									÷÷			+
= ò									-		2		)dx = ç16arcsinç										÷	+ 8sin(2arcsinç									÷÷			+
	0										2					è				è	2 2		ø					è			2 2		øø	0
	1		2(8 - x2 )3 / 2									x3			2					32
				2		2										2
				2		2		+ (-4x +								2						2
+		×												)			= 8p -						(куб.ед.).
+	2	×	3	0								6		)	0		= 8p -				3		(куб.ед.).
	2		3	0								6			0						3

Задания для контрольной работы № 4

221–230. Найти область определения функции. Изобразить решение на координатной плоскости.

221.

z =

2 + x - y ln(1 + x) .

226.

z = ln x + ln( y - 2x +1) .

222.

z =

ln(1 + y) .

227.

z = ln(x2 + y 2 -1) .

3 + x - y

223.

z =

+ ln(x - y) .

228.

z =

x2 + y2 -16

224.

z =

2 + x - y ln(x2 + y) .

229.

z =

xy +

z = ln(9 - x2 - y 2 ) .

x +1

225.

230.

z =

+ ln(x + y) .

231–240.

Найти частные производные z¢x

и z¢y

функции двух

переменных

z = f (x; y) :

231.

z = ( x + 2)3 + ln y .

236.

z =

x + y

232.

z = sin(xy) + y 2 .

237.

z =

- y

233.

z = (x + y 2 ) × e x .

238.

z =

ln(x + y)

x - y

z =

x + y

z =

ex + y

234.

239.

cos y

3 - y

235.

z =

+ ex .

240.

z =

+ e y .

241–250. Составить уравнение касательной плоскости и уравнения нормали к поверхности в данной точке M 0 (x0 ; y0 ; z0 ) .

241.	z = x2	+ y 2	- 4 ,	M0 (-2;1;1).	246.	z = 3 - x2 - ( y -1)2 , M 0 (1;2;1) .
242.	z = x2	+ y 2	- 2 ,	M0 (1;2;3) .	247.	z = x2 + y 2 + 3	,	M 0 (1;-2;8) .
243.	z = ( x +1)2 + ( y -1)2 ,			M0 (1;2;5) .	248.	z = x2 + y 2 +1	,	M 0 (-1;2;6) .
244.	z = 4 - x2 - y2 ,			M 0 (1;1;2) .	249.	z = (x - 2)2 + y 2 ,		M 0	(3;-2;5) .
245.	z = x2	+ y 2	-1,	M 0 (2;2;7) .	250.	z = 2x2 + y 2 ,		M 0	(-1;2;6) .

251–260. Исследовать функцию двух переменных z = f (x; y) на экстремум.

251.	z = x3 - 2 y 2 - 3x + 6 y +1.			256.	z = x3 - 4 y2 - 3x +12y -1.
252.	z = x2 - 4 y3 - 2x +12 y .			257.	z = x3 + 3y3 - 3x - 9 y 2 + 16 .
253.	z = 2x3 + 2 y3 - 6xy + 5 .			258.	z = -x2 + xy - y2 - 9x + 3 y - 20 .
254.	z = x3 + 3xy 2 -15x -12 y +1.			259.	z = 12xy - x2 y - xy 2 .
255.	z = -3x2 - 3y 2 + 6(x - y) .			260.	z = x3 + 8 y3 - 6xy +1.
261–270. Найти градиент функции z = f (x; y) в точке M 0 (x0 ; y0 ) .
261.	z = x2	- 2xy - y 2 , M 0 (1;2) .		266.	z = x2 + xy + y2 + 3 ,	M 0 (3;0) .
262.	z = x3	- xy + y 2 + 4 ,	M 0 (2;1) .	267.	z = 2x3 - x2 + y3 - y ,	M0 (-1;2) .
263.	z = x2	+ xy - y3 ,	M0 (0;-3) .	268.	z = x 2 - xy 2 + y 2 ,	M 0 (1;1) .
264.	z = x4	+ x2 y + y3 ,	M0 (2;-1) .	269.	z = x3 - x2 y 2 + 4 y3 ,	M 0 (1;1) .
265.	z = 2x2 + 4xy - 3y3 ,		M 0 (-3;1) .	270.	z = -x2 - 5xy + 2 y 2 ,	M 0 (1;-3) .

271–280. При помощи двойного интеграла вычислить площадь фигуры, ограниченной данными линиями. Сделать чертеж.

271.

y = x2 ,

y =

0 £ x £ 2 .

276.

y = x3 ,

y = 4x,

x ³ 0 .

272.

y = x,

y =

x = 4 .

277.

y = x,

y = -x,

y = 2 .

273.

x + y = 5, y =

278.

y = 1,

y = 6, y =

, x = 0 .

y = x3 ,

y = ( x +1)2 -1,

274.

x + y = 2,

y = 0 .

279.

y = 0 .

275.

x = ( y -1)2 -1,

x = 3 .

280.

y2 = x,

x + y = 2,

x = 0 .

281–290. Найти объем тела, ограниченного поверхностями. Сделать чертеж.


281.	2x + 3y + 2z - 6 = 0, x = 0,					y = 0,	z = 0 .
282.	y =1 + x2 , z = 3x,		z = 0,		y = 5 (при		z ³ 0 ).
283.	x2 + y2 = 8,	x = 0, y = 0,			z = 0, x + y + z = 4 .
284.	z = x - y +1,	x = 0, y = 0, z = 0 .
285.	z = 4 - x2 ,	2x + y = 4,		x = 0,		y = 0,	z = 0 .
286.	x2 + 4 y2 =1 - z,		z = 0 .
287.	z = 2x + y + 2,		x = 0, y = 0, z = 0 .
288.	x2 + 9 y2 = 3 - z,		z = 0 .
289.	2x + y - 3z = 6, x = 0,			y = 0,		z = 0.
290.	x + 2 y - z - 4 = 0, x = 0,			y = 0, z = 0.

Вопросы к экзамену

1.Задачи, приводящие к понятию дифференциальных уравнений.

2.Дифференциальные уравнения с разделяющимися переменными.

3.Линейные дифференциальные уравнения первого порядка.

4.Однородные и неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

5.Числовые ряды. Необходимый признак сходимости ряда.

6.Гармонический и обобщенный гармонический ряды.

7.Признаки сравнения числовых рядов.

8.Признак Даламбера.

9.Функциональный ряд. Радиус сходимости степенного ряда. Теорема Абеля.

10.Применение функциональных рядов в приближенных вычислениях.

11.Функция двух переменных: область определения, множество значений.

12.Понятие частных производных функции двух переменных.

13.Нахождение частных производных от функции двух переменных, заданной неявно.

14.Определение дифференциала функции двух переменных.

15.Уравнение касательной плоскости и уравнения нормали к поверхности, заданной в виде F (x; y; z) = 0 .

16.Нахождение экстремума функции двух переменных.

17.Определение градиента функции двух переменных и его вычисление.

18.Понятие двойного интеграла.

19.Способ вычисления двойного интеграла.

20.Нахождение площади фигуры с помощью двойного интеграла.

21.Вычисление объема тела с помощью двойного интеграла.

Библиографический список

1.Письменный Д. Т. Конспект лекций по высшей математике: учеб. для вузов. – М. : Рольф, 2001. – 280 с.

2.Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в уп-

ражнениях и задачах. : учеб. пособие для студентов втузов. – 3-е изд., перераб.

и доп. – М. : Высш. шк., 2003. – Ч. 2. – 379 с.

3. Филиппов А. В. Сборник задач по дифференциальным уравнениям:

учеб. пособие для студентов втузов. – Ижевск : НИЦ «Регулярная и хаотиче-

ская динамика», 2000. – 176 с.

Учебное издание

Величко Татьяна Владимировна Завьялова Татьяна Викторовна Пирогова Ирина Николаевна

МАТЕМАТИКА

ЧАСТЬ II

Учебно-методическое пособие для студентов технических специальностей заочного отделения, обучающихся по ускоренной программе

Издание третье, исправленное и дополненное

Редактор С. В. Пилюгина

Подписано в печать 20.11.2010 г. Формат 60 × 84 / 16 Бумага офсетная. Усл. печ. л. 3,3

Тираж 300 экз. Заказ № 160

Издательство УрГУПС 623034, Екатеринбург, ул. Колмогорова 66

<<< < Предыдущая 1 2 3 45 / 55

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.03.2016742.91 Кб50Маршрутные карты.doc
#
17.05.2015518.98 Кб35матан.pdf
#
17.05.2015490.79 Кб26матем 1 уск 2009.pdf
#
17.05.201511.02 Кб18Матем.docx
#
17.05.2015632.36 Кб40математика II 2008 6 лет.pdf
#
17.05.2015457.66 Кб26математика ч 2.pdf
#
17.05.2015664.38 Кб37Математика ч.2.pdf
#
17.05.2015637.39 Кб56Математика.pdf
#
17.05.2015673.66 Кб25математика.pdf
#
17.05.20151.44 Mб27Материалка.pdf
#
17.05.20153.84 Mб253матмоделирование.doc