
математика II 2008 6 лет
.pdf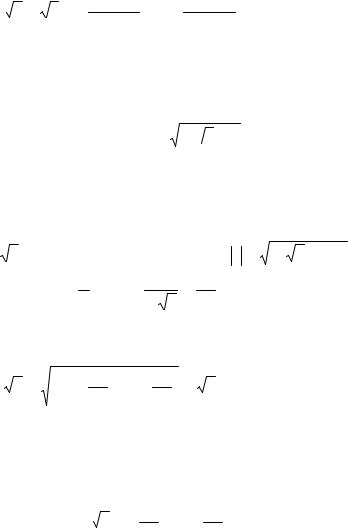
zn = rn (cos nϕ +i sin nϕ) ; |
|
||
n z = n r (cos |
ϕ + 2πk |
+i sin |
ϕ + 2πk ) , |
|
n |
|
n |
где k = 0,1,2,..., n −1.
Примеры
1.Найти все значения корня 3 (− 3 +i) и изобразить их на комплексной плоскости.
3 +i) и изобразить их на комплексной плоскости.
Решение
Найдем аргумент и модуль комплексного числа
z = − 3 +i . |
|
|
|
|
|
|
|
|
|
|
z = (− 3)2 +12 = 2 , |
|||||||
ϕ = arg z = arctg |
y |
= arctg |
− |
1 |
3 |
= |
5π . Тогда по формуле из- |
|||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
6 |
|
|
|
|||
влечения корня имеем |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5π |
|
|
|
|
|
|
|
|
|
5π |
|
|
5π |
|
|
|
|
|
+ 2πk |
|
|
3 |
z |
= 3 2(cos |
+ i sin |
) = |
3 |
2(cos |
6 |
+ |
||||||||||
|
|
|
6 |
|
6 |
|
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
5π |
+ 2πk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+i sin |
6 |
). Найдем все значения корня |
|
|||||||||||||||
|
|
|||||||||||||||||
|
3 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = 0 z |
|
= 3 2(cos 5π |
+ i sin 5π ), |
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
18 |
|
|
|
|
18 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
51
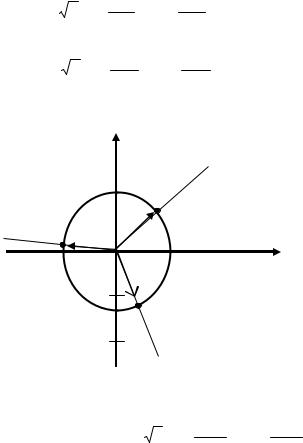
k =1 z2 |
= 3 |
2(cos |
17π |
+i sin |
17π ), |
|
|
|
||||||
|
|
|
|
18 |
|
18 |
|
|
|
|
||||
k = 2 z3 |
= 3 |
2(cos |
|
29π |
+i sin 29π ). |
Изобразим эти |
||||||||
|
|
|
|
18 |
|
18 |
|
|
|
|
||||
числа на комплексной плоскости (рис.12). |
|
|
||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 |
|
|
500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1700 |
Z2 |
|
|
|
|
|
|
|
1,25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2900 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 12 |
|
|
|
|
|
|
||
2. Вычислить (i −1) |
4 |
|
π i |
+ |
|
|
− 2π |
+i sin |
− 2π |
|||||
|
+ 4e 6 |
4 3 cos |
|
3 |
3 |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ записать в алгебраической, тригонометрической и показательной формах.
Решение
Представим данное выражение в виде суммы трех ком-
|
|
|
|
|
|
π |
|
плексных чисел: |
z 4 |
, где z = i −1 |
= −1 +i |
; z |
2 |
= 4e 6 i |
; |
|
1 |
1 |
|
|
|
|
|
|
|
52 |
|
|
|
|
|
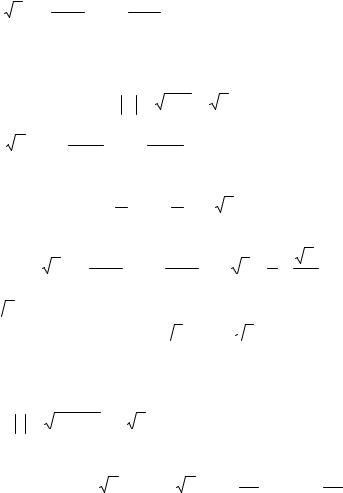
z3 |
= 4 3(cos |
−2π |
+i sin |
−2π ) . |
|
|
|
|
|
||
|
|
|
3 |
|
3 |
|
|
|
|
|
|
Преобразуем данные числа: |
|
|
|
|
|
|
|||||
|
z |
= (−1 +i) . |
z = |
1 +1 = |
2 , |
ϕ = |
3π |
. |
Тогда |
||
|
|
||||||||||
|
1 |
|
|
|
1 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 4 |
= ( |
2)4 (cos 3π 4 +i sin 3π 4) = 4(cos(π) + i sin(π)) = −4 . |
|||||||||
1 |
|
|
4 |
4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
π |
|
+i sin π ) = 2 |
|
|
|
|
|
|
|
z2 |
= 4e |
6 i = 4(cos π |
3 + 2i . |
|
|
|
||||
|
|
|
|
6 |
|
6 |
|
|
|
|
|
|
z3 |
= 4 |
3(cos |
− 2π |
+i sin |
−2π ) = 4 |
3(− 1 |
− |
3i ) = |
|
|
|
|
|
|
3 |
|
3 |
|
2 |
|
2 |
|
= −2 3 − 6i .
3 − 6i .
z = z14 + z2 + z3 = − 4 + 2 3 + 2i −2
3 + 2i −2  3 −6i = −4 − 4i .
3 −6i = −4 − 4i .
Мы нашли алгебраическую форму данного выражения. Запишем тригонометрическую и показательную формы:
z = 16 +16 = 4 2 ; ϕ = − |
3π |
. |
|
|
||
4 |
|
|
||||
Окончательно имеем |
|
|
|
|||
|
|
|
|
|||
|
3π |
|
|
3π ) +i sin(− |
3π )) . |
|
z = −4 − 4i = 4 2e− |
|
i = 4 2(cos(− |
||||
4 |
||||||
|
|
|
|
|
4 |
4 |
Осталось изобразить это число на комплексной плоскости (рис.13).
53
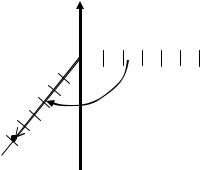
y
 x 0
x 0
ϕ
Z
Рис. 13
2.Дифференциальные уравнения первого порядка
Дифференциальным уравнением называется уравне-
ние, связывающее независимую переменную x , искомую функцию y и производные этой функции. Общий вид диф-
ференциального уравнения F(x, y, y′, y′′,..., y(n) ) = 0 . Поря-
док ( n ) старшей производной, входящей в уравнение, назы-
вается порядком дифференциального уравнения.
Рассмотрим уравнения первого порядка. Оно связывает независимую переменную х, искомую функцию y и ее первую производную y′. Поэтому в общем виде его можно за-
писать так: F(x, y, y′) = 0 . Разрешая его, если это возможно, относительно производной y′, получим y′ = f (x, y) . Реше-
нием дифференциального уравнения первого порядка назы-
вается всякая функция y =ϕ(x) , которая при подстановке
ее |
в |
уравнение |
обращает |
его |
в |
тождество: |
F |
|
′ |
График решения дифференциального |
|||
(x,ϕ(x),ϕ (x)) ≡ 0 . |
||||||
уравнения называется интегральной кривой. Общим реше-
нием уравнения первого порядка называется функция y =ϕ( x,C ) , зависящая от x и произвольной постоянной C ,
54
если она удовлетворяет таким условиям: 1) она является решением дифференциального уравнения при любом допустимом значении постоянной С; 2) каково бы ни было начальное условие y( x0 ) = y0 , найдется такое значение
С = С0 , что функция y =ϕ( x,C0 ) удовлетворяет этому начальному условию, т.е. y(x0 , С0 ) = y0 . Если общее решение
дифференциального уравнения найдено в виде, не разрешенном относительно y , т.е. в виде Ф(x, y, C) = 0 , то оно
называется общим интегралом дифференциального уравнения. Частным решением дифференциального уравнения первого порядка называется функция y =ϕ( x,C0 ) , кото-
рая получается из общего решения, если произвольной постоянной С придать определенное значение C = C0 . Гео-
метрически общее решение y =ϕ( x,C ) представляет собой семейство интегральных кривых на координатной плоскости. Кривая семейства, проходящая через точку M 0 ( x0 , y0 ) ,
представляет график частного решения y =ϕ( x,C0 ) . Рас-
смотрим три типа дифференциальных уравнений первого порядка.
2.1.Уравнения с разделяющимися переменными
Такое уравнение может быть представлено в виде dydx = f ( x )g( y ) . Чтобы решить такое уравнение, его следу-
ет преобразовать к виду, в котором дифференциал и функция переменной x окажутся в одной части равенства, а переменной y – в другой. Затем проинтегрировать обе части полученного равенства.
55
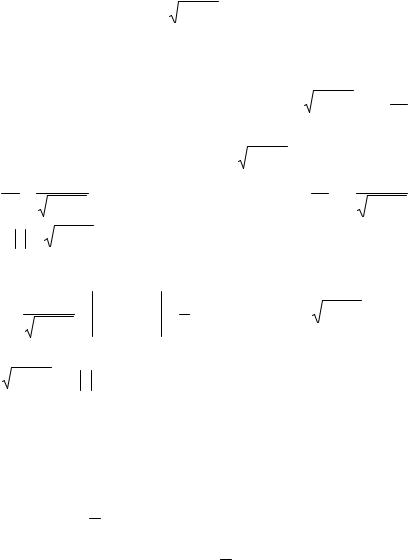
Пример
Решить уравнение 1 + y2 = xyy′.
Решение
|
Представим y′ |
как отношение дифференциалов : |
|||||||
y′ |
dy |
|
|
|
|
|
|
2 |
dy |
= dx |
и подставим в исходное уравнение |
1 + y |
|
= xy dx . |
|||||
Разделим переменные. |
Для этого умножим обе части урав- |
||||||||
нения |
на dx , разделим на |
х, |
1 + y2 . |
Тогда |
|
получим |
|||
dx |
= |
ydy 2 . |
Интегрируя, |
найдем |
∫dx = |
∫ |
ydy 2 , |
||
x |
1 + y |
|
|
|
|
x |
|
1 + y |
|
ln x = |
1 + y2 |
+ C . При этом, если |
интеграл в левой части |
||||||
был табличным, то второй интеграл можно было вычислить отдельно:
|
ydy |
= u =1 + y2 |
= |
1 |
du1 |
= |
2 u |
1 |
+C = 1 + y2 |
+C . |
||
|
2 |
|||||||||||
∫ |
1 + y2 |
du = 2 ydy |
|
2 |
∫u |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||||||||
Общее решение получили в виде общего интеграла
1 + y2 − ln x + C = 0 .
2.2.Однородные дифференциальные уравнения
Дифференциальное уравнение первого порядка называется однородным, если оно может быть представлено в
виде y′ = g( xy ) . Для решения данного уравнения вводят
вспомогательную функцию z = xy . Это позволяет свести ис-
ходное уравнение к уравнению с разделяющимися перемен-
56
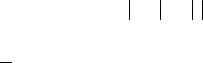
ными. Так как |
y = zx , |
y |
′ |
|
|
|
′ |
|
|
|
|
|
|
|
|
||||||||
|
= z x + z , то уравнение примет вид |
||||||||||||||||||||||
|
′ |
|
|
|
|
|
|
|
|
dz |
|
|
dx |
|
|
|
|
|
|
||||
|
z x + z = g( z ) , |
откуда |
|
|
= x . |
|
|
|
|
|
|
||||||||||||
g(z) − z |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Пример |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Решить уравнение y |
′ |
= |
|
x + 2 y |
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Преобразуем |
|
правую |
|
|
часть |
уравнения |
||||||||||||||
|
x + 2 y |
=1 + 2 |
y |
. Теперь очевидно, что мы имеем однород- |
|||||||||||||||||||
|
|
|
|
x |
|||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
′ |
|
|
|
|
ное |
уравнение |
первого |
|
|
порядка, |
|
|
=1 + 2 x |
. Положим |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
′ |
|
|||
|
z = |
x . Тогда |
будем иметь |
|
|
|
|
|
|
|
=1 + z , или |
||||||||||||
|
|
z x + z =1 + 2z , z x |
|||||||||||||||||||||
|
xdz |
=1 + z . Разделим переменные |
|
|
dz |
|
= dx . Проинтегри- |
||||||||||||||||
|
dx |
1 |
+ z |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||||
руем данное уравнение и получим ln1 + z = ln x + ln C , или 1 + z = Cx . Возвращаясь к первоначальным переменным,
запишем ответ: 1 + xy = Cx .
Откуда y = Cx2 − x .
2.3.Линейные дифференциальные уравнения
Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид y′+ p(x) y = q(x) . Ес-
ли q(x) = 0 , то уравнение называется линейным однород-
ным, в противном случае – неоднородным. Одним из способов решения этого уравнения является поиск решения в ви-
57
де |
y = u( x )v( x ) . Так |
как y |
′ |
′ |
|
|
′ |
, то получаем |
||
|
= u v + uv |
|
||||||||
′ |
|
′ |
+ p(x)uv = q(x) |
′ |
+ u(v |
′ |
+ p(x)v) = q(x) . Най- |
|||
u v + uv |
|
или u v |
|
|||||||
дем сначала какое-либо частное решение v = v( x ) из уравнения v′+ p(x)v = 0 . Тогда функция u = u( x ) – решение уравнения u′v = q(x) . Таким образом, решение исходного
уравнения сводится к решению двух уравнений с разделяющимися переменными.
|
|
|
Пример |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Решить уравнение xy′− 2 y = 2x4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Разделим |
обе |
|
части |
уравнения на |
|
x . |
Тогда |
данное |
|||||||||||||||||||||||||||||||
уравнение примет вид y′− 2 |
y |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
y = uv , |
|
||||||||||||||||||||||
|
= 2x |
|
. Пусть |
тогда |
||||||||||||||||||||||||||||||||||||||
x |
|
|||||||||||||||||||||||||||||||||||||||||
y |
′ |
|
|
′ |
|
+ uv |
′ |
и |
|
исходное |
уравнение |
|
примет |
вид |
||||||||||||||||||||||||||||
|
= u v |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
′ |
|
|
|
|
′ |
− |
|
|
|
uv |
= 2x |
3 |
|
|
′ |
(v |
′ |
− |
|
v |
|
|
u |
= 2x |
3 |
|
|
|
||||||||||||||
|
|
|
|
2 |
|
x |
|
, |
или |
2 x ) |
|
. |
Множи- |
|||||||||||||||||||||||||||||
u v + uv |
|
|
|
|
u v + |
|
|
|
||||||||||||||||||||||||||||||||||
тель v(x) |
будем искать так, чтобы он был частным решени- |
|||||||||||||||||||||||||||||||||||||||||
ем дифференциального уравнения |
|
v′− 2 |
|
v |
= 0 , |
т.е. чтобы |
||||||||||||||||||||||||||||||||||||
|
|
x |
|
|||||||||||||||||||||||||||||||||||||||
коэффициент |
перед |
u(x) был |
бы |
|
|
равен |
нулю. |
|
Тогда |
|||||||||||||||||||||||||||||||||
dv |
= 2 |
v |
|
, |
откуда dv |
= 2 dx . Проинтегрировав, |
найдем ча- |
|||||||||||||||||||||||||||||||||||
dx |
x |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
v |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или v = x2 . |
|||||||||||||
стное решение этого уравнения ln |
|
v |
|
= 2 ln |
|
x |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
′ |
|
Найдем |
общее |
решение |
|
|
|
оставшегося |
|
уравнения |
||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
, |
|
|
подставив |
в |
него |
найденное |
|
v . |
|
Получим: |
||||||||||||||||||||||||||
u v = 2x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
′ |
2 |
= 2x |
3 |
|
или du = |
2xdx . Тогда u = x |
2 |
|
+C . Теперь мож- |
|||||||||||||||||||||||||||||||
|
u x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
но написать общее решение исходного уравнения. Оно будет иметь вид y = x2 ( x2 +C ) . Пусть нам дано начальное условие y(1) =1. Тогда из найденного общего решения вы-
58
делим частное решение, удовлетворяющее заданному начальному условию: 1 =12 (12 + C) . Отсюда С=0 и частное решение равно y = x4 .
3.Дифференциальные уравнения второго порядка, допускающие понижение порядка
Общим решением дифференциального уравнения второго порядка F( x, y, y′, y′′) = 0 называется функция
y = ϕ( x,C1 ,C2 ) , зависящая от двух произвольных постоянных. Для нахождения частного решения задают начальные условия y( x0 ) = y0 , y′( x0 ) = y0′ .
В некоторых случаях решение дифференциального уравнения второго порядка может быть сведено к последовательному решению двух дифференциальных уравнений первого порядка. Тогда говорят, что данное дифференци-
альное уравнение допускает понижение порядка. Рассмот-
рим некоторые виды дифференциальных уравнений второго порядка, допускающие понижение порядка.
1. Если дифференциальное уравнение имеет вид y′′ = f ( x ) , то оно решается последовательным интегриро-
ванием.
Пример
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям:
y |
′′ |
= xe |
−x |
′ |
|
|
, y( 0 ) =1, y ( 0 ) = 0 . |
Решение
Найдем общее решение последовательным интегрированием данного уравнения:
59

y′′ = ddxy′ = xe−x ;
y′ = ∫xe−x dx = |
|
u = x |
du = dx |
|
= −xe−x + ∫e−x dx = |
||
|
|
||||||
|
dv = e |
−x |
dx |
v = −e |
−x |
||
|
|
|
|
|
|||
= −xe−x − e−x +C1 .
Найдем постоянную C1 , использовав второе начальное условие. 0 = 0 e0 − e0 +C1 . Откуда C1 =1 . Продолжим ре-
шение y′ = dydx = −xe−x − e−x +1 . Проинтегрировав обе части,
получим y = xe−x + e−x + e−x |
+ x +C2 . Используя первое на- |
|||||
чальное условие, найдем C2 : 1 = 0 e0 |
+ 2e0 |
+ 0 +C2 . Тогда |
||||
C2 = −1. |
И |
искомое |
частное |
решение |
рав- |
|
но: y = xe−x + 2e−x + x −1. |
|
|
|
|
||
2. Если уравнение не содержит явным образом иско- |
||||||
мую функцию |
y( x ), т.е. |
дифференциальное уравнение |
||||
имеет вид |
F( x, y′, y′′) = 0 , то такое уравнение можно ре- |
|||||
шить, введя вспомогательную переменную |
y′ = p(x) . То- |
|||||
гда y′′ = p′. Таким образом, |
порядок уравнения понизится |
|||||
на единицу. После чего нужно решить дифференциальное уравнение первого порядка соответствующего вида.
Пример
Найти общее решение дифференциального уравнения xy′′ = y′ln yx′ .
Решение
Пусть |
y′ = p |
|
и |
y′′ = p′. |
Уравнение примет вид |
|||||
xp′ = p ln |
p |
или p′ |
= |
|
p |
ln |
p |
. Получили однородное диффе- |
||
x |
|
|
x |
x |
||||||
|
|
|
|
|
|
|
|
|
60 |
|
