математика II 2008 6 лет

2.Найти длину дуги кривой x = 2 cos3 t, y = 2sin3 t

при 0 ≤ t ≤ π4 .

Решение

Найдем производные функций x(t), y(t) :

xt′ = −6 cos2 t sin t , yt′ = 6 sin2 t cos t . Подставим их в формулу и получим

криволинейной трапеции, ограниченной непрерывной кривой y = f (x) , осью Оx и прямыми x = a и x = b , вычисля-

b

ется по формуле Vox =π∫ f 2 (x)dx (рис. 8).

a

41

Рис. 8

Если криволинейная трапеция ограничена графиком непрерывной функции x = ϕ( y ) и прямыми x = 0, y = c и

y = d( c < d ) , то объем тела, полученного вращением этой трапеции вокруг оси Oy, будет равен

d

Voy = π∫ϕ2 ( y)dy .

c

Пример

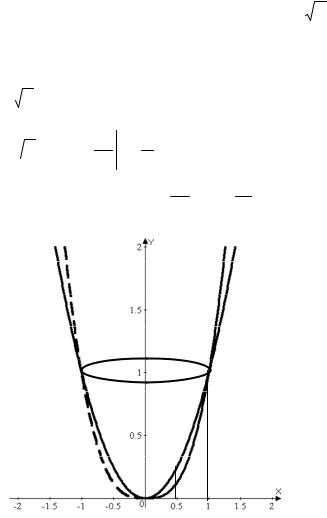
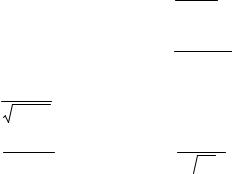
Найти объем тела, полученного от вращения вокруг оси ординат плоской фигуры, ограниченной линиями y = x2 , y = x3 .

Решение

Сделаем рисунок (рис. 9) и убедимся, что искомый объем получится в результате разности двух объемов: объема V1 , полученного от вращения вокруг оси Oy фигуры,

ограниченной линиями x = 3 y , x = 0, y =1, и объема тела

42

221 – 230. Найдите длину дуги с помощью определенного интеграла.

221.Кривой y =1 −ln cos x , ( 0 ≤ x ≤ π4 ).

222.Кривойx = 5(t −sin t) , y = 5(1 −cos t), ( 0 ≤ t ≤ π ).

223.Кривой y = ln(sin x) , ( π4 ≤ t ≤ π2 ).

224. Кривойx = 4(cost +t sin t) , y = 4(sin t −t cost) ,

227.Кривой x = −ln(cos y) , ( 0 ≤ y ≤ π3 ).

228.Кривой x =10 cos3 t , y =10sin3 t , ( 0 ≤ t ≤ π2 ).

229.Кривой y = ln x , ( 43 ≤ x ≤ 125 ).

230. Кривой x = 3(t −sin t) , y = 3(1 −cost),

( 0 ≤ t ≤ 2π ).

231 – 240. Вычислите объем тела, образованного вращением вокруг указанной оси фигуры, ограниченной заданными линиями.

231.Вокруг оси Ох фигуры, ограниченной линиями y = 2x − x2 , y = 2 − x, x = 0 .

232.Вокруг оси Оy фигуры, ограниченной линиями

y = x2 , y = x2 , y = 4, x ≥ 0 . 4

45

233.Вокруг оси Оy фигуры, ограниченной линиями y2 = x −1, y = 0, y =1, x = 0,5, x ≥ 0 .

234.Вокруг оси Ох фигуры, ограниченной линиями y = 2x2 , y2 = 4x .

235.Вокруг оси Оy фигуры, ограниченной линиями y2 = 4x , y ≥ 0, x =1.

236.Вокруг оси Ох фигуры, ограниченной линиями x = 4, y = x, y = 2 x .

237.Вокруг оси Ох фигуры, ограниченной линиями y = sin x, y = 3sin x, 0 ≤ x ≤π .

238.Вокруг оси Ох фигуры, ограниченной линиями

x = 0,5, y = 0, y =1, y = x −1 .

239.Вокруг оси Оy фигуры, ограниченной линиями y = 0, y = 2x − x2 .

240.Вокруг оси Оy фигуры, ограниченной линиями x = 2, y = 0, y = x2 .

IV. КОМПЛЕКСНЫЕ ЧИСЛА. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

1. Комплексные числа

Комплексным числом называется выражение вида z = x + iy , где x, y – действительные числа; i – мнимая еди-

ница, удовлетворяющая равенству i2 = −1. Такая форма записи комплексных чисел называется алгебраической формой. Число x называется действительной частью числа

Re(z) = 0 , тоz = 0 +iy = iy . В этом случае комплексное чис-

46

ло z = iy называется чисто мнимым. Числа z = x + iy и z = x −iy называются сопряженными комплексными числа-

ми. Два комплексных числа называются равными, если их действительные и мнимые части соответственно равны.

Арифметические операции над комплексными числами

Пусть даны два комплексных числа z1 = x1 + iy1 , z2 = x2 + iy2 .

z1 ± z2 = ( x1 ± x2 ) + i( y1 ± y2 ) .

z z = x2 + y2 , т.е. произведение сопряженных комплексных

чисел равно действительному числу.

3. Частным двух комплексных чисел называется ком-

Примечание. Заметим, что запоминать эту формулу не стоит. При делении двух комплексных чисел достаточно домножить числитель и знаменатель на число, сопряженное знаменателю. Этот алгоритм деления комплексных чисел продемонстрирован на примере.

Пример

Даны два комплексных числа z1 = 2 + 5i и z2 = 3 − 4i .

Найти z1 ± z2 , z1 z2 , z1 . z2

47

Решение

z1 + z2 = 2 + 3 + i( 5 − 4 ) = 5 + i .

z1 − z2 = ( 2 − 3) + i( 5 + 4 ) = −1 + 9i .

z1z2 = ( 2 + 5i )( 3 − 4i ) = 6 +15i −8i − 20i2 = 26 + 7i .

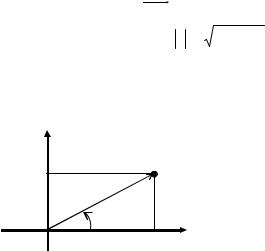
Комплексное число z = x + iy можно изобразить на плоскости Oxy точкой М(x, y) , а можно вектором, начало

ные числа, называется комплексной плоскостью и обозначается символом ( z ). Длина вектора ОМ называется модулем комплексного числа и обозначается r = z = x2 + y2 .

Ось Ox, на которой изображаются действительные числа, называется действительной осью, а ось Oy, на которой изображаются чисто мнимые числа z = iy , – мнимой

осью (рис. 10).

Рис. 10 48

Тригонометрическая и показательная формы комплексного числа

Угол, образованный радиус-вектором OМ с осью Ox,

называется аргументом комплексного числа z и обознача-

ется ϕ = arg z . Значение аргумента ϕ определяется неоднозначно, с точностью до слагаемого вида ϕ = 2πn . Значение угла ϕ , удовлетворяющее условию −π <ϕ ≤ π , назы-

вается главным значением аргумента. Это значение может быть найдено из формул sinϕ = xr , cosϕ = ry , tgϕ = xy .

Из рис. 10 очевидно, что x = r cos ϕ, y = r sin ϕ, откуда

комплексное число z можно представить в виде

z = r(cos ϕ+i sin ϕ) . Такая форма комплексного числа назы-

вается его тригонометрической формой.

Кроме того, комплексное число можно записать в по-

казательной форме z = reiϕ .

Пример

Решить уравнение z2 − 2z + 4 = 0 и представить его корни в алгебраической, тригонометрической и показательной формах. Изобразить их на комплексной плоскости.

Решение

Найдем корни квадратного уравнения

z2 + 2z + 4 = 0 ,

числа в двух других формах. Для этого найдем их модули и аргументы:

Изобразим эти корни на комплексной плоскости (рис. 11).

y

Z1 π

3

x 0

− π

Z2 3

Рис. 11

Кроме того, приведем формулы возведения в степень комплексных чисел (формула Муавра), а также извлечения корней из них.

50