
математика II 2008 6 лет
.pdf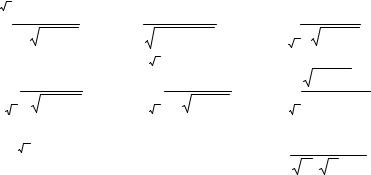
191 – 200. В заданиях вычислить интеграл ∫b |
f (x)dx по |
a |
|
формуле Ньютона-Лейбница, используя метод подстановки.
|
3 |
|
2 dx2 |
|
|
|
|
1 |
|
x2+1 |
|
|
|
|
|
2 |
|
dx2 |
|
|
|
||||
191. |
∫ |
x |
+ |
. |
192. ∫ |
|
|
3 dx . |
193. |
|
∫ |
|
|
. |
|
||||||||||
|
1 |
x |
|
1 |
|
0 |
( x |
|
+1) |
|
|
|
|
2 x x |
|
−1 |
|
||||||||
|
4 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
2 |
|
|
dx |
|
2 . |
|
|
1 − x2 |
dx |
|
|||||||
194. |
∫ |
|
x x |
2 |
− |
. |
195. |
∫ |
x |
2 |
1 |
− x |
196. |
|
∫ |
|
x |
2 |
|
. |
|||||
|
2 2 |
|
4 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
e |
|
dx |
|
|
|
|
|
81 |
|
|
4dx |
|
|
|
|
||
197. |
∫e |
x dx . |
|
|
198. ∫ |
|
|
|
|
. |
|
199. ∫ |
|
|
|
|
|
. |
|||||||
|
|
x(5 |
−4 ln x) |
2 |
|
|
|
|
|
|
|||||||||||||||
|
0 |
|
|
|
|
|
|
1 |
|
|
|
16 |
|
x ( |
x +1) |
|
|||||||||
200. |
1 ( arctgx − 3)2 |
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∫ |
|
1 + x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
31
III. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
1. Несобственный интеграл I рода
Пусть функция f ( x ) определена и непрерывна на промежутке [a;+∞). Если существует конечный предел
b
lim ∫ f ( x )dx , то его называют несобственным интегралом
b→+∞ a
+∞
первого рода и обозначают ∫ f ( x )dx . В этом случае гово-
a
рят, что несобственный интеграл сходится. Если указанный предел равен бесконечности или не существует, то интеграл
расходится.
Аналогично определяют несобственный интеграл на
b |
b |
промежутке (− ∞;b]: ∫ f ( x )dx = alim→−∞ ∫ f (x)dx . |
|
−∞ |
a |
Несобственный интеграл с двумя бесконечными пределами определяется формулой
+∞ с +∞
∫ f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx ,
−∞ −∞ с
где с– произвольное число. В этом случае интеграл сходится лишь тогда, когда сходятся оба интеграла справа.
Отметим, |
что если непрерывная функция f ( x ) ≥ 0 |
|
|
[a;+∞) |
+∞ |
на промежутке |
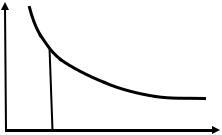
и интеграл ∫ f ( x )dx сходится, то |
|
a
геометрически он равен площади бесконечно длинной криволинейной трапеции (рис. 2).
32
y |
|
||
|
|
у=f(x) |
|
0 |
|
|
x |
|
a |
|
|
|
|
Рис. 2 |
|
2. Несобственный интеграл II рода |
|
||
Пусть функция f ( x ) определена и |
непрерывна на |
||
промежутке [a;b) и имеет бесконечный разрыв при x = b .
b−ε
Если существует конечный предел limε→0 |
∫ f (x)dx (ε > 0) , то |
|
a |
его называют несобственным интегралом второго рода и
b
обозначают ∫ f ( x )dx . Если предел в правой части сущест-
a
вует, то несобственный интеграл сходится. Если этот предел равен бесконечности или не существует, то интеграл
расходится.
Аналогично, если функция f ( x ) терпит бесконечный
b |
b |
разрыв в точке x = a , то полагают ∫ f ( x )dx = limε→0 |
∫ f (x)dx . |
a |
a+ε |
Если функция терпит разрыв во внутренней точке с отрезка [a;b], то несобственный интеграл второго рода оп-
33

b c b
ределяется формулой ∫ f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx . В
a a c
этом случае интеграл называется сходящимся, если оба несобственных интеграла, стоящие в правой части равенства, сходятся.
Примеры
Вычислить несобственные интегралы или установить их расходимость.
+∞dx
1. ∫1 x3 .
Решение
+∞dx |
|
|
|
|
|
|
b |
dx |
|
|
|
1 |
|
|
b |
1 |
|
|
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
∫1 |
|
|
|
= lim |
|
∫1 |
|
|
= lim |
|
− |
|
|
|
= − |
|
(0 |
− |
1) = |
|
|||||
x3 |
|
|
x3 |
2x2 |
2 |
2 |
|||||||||||||||||||
|
|
|
b→+∞ |
b→+∞ |
|
|
|
1 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
∫ |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
x ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
dx |
|
|
= lim |
2 |
d ln x |
= −lim(ln(ln x) |
|
2 |
= |
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||||||||||
1 |
x ln x |
|
1+ε |
ln x |
|
|
|||||||||||||||||||
|
|
|
ε |
→0 |
|
|
ε→0 |
|
|
|
|
1+ε |
|
|
|
||||||||||
∫ |
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|||||
=−(ln ln 2 −lim ln ln(1 +ε)) = −∞ .
ε→0
Интеграл расходится.
34
3.Вычисление площадей плоских фигур в декартовой системе координат
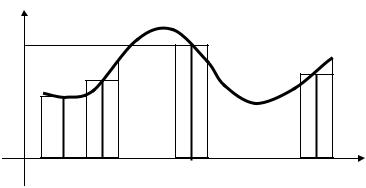
Исходя из геометрического смысла определенного интеграла площадь криволинейной трапеции, расположенной выше оси абсцисс ( f ( x ) ≥ 0 ), равна соответствующему оп-
ределенному интегралу (рис.3):
b |
|
S = ∫ f ( x )dx . |
|
a |
|
y |
y=f(x) |
f(ci) |
|
|
0 a c1 x1 c2 x2 |
xi-1 |
ci xi |
cn b |
x |
|
|
|
|
Рис.3 |
|
|
|
|
В общем случае площадь фигуры, ограниченной кри- |
|||||
выми y = f1( x ) и y = f2 ( x ) , прямыми x = a и x = b , |
при |
|||||
|
|
|
|
b |
|
|
условии, что |
f2 ( x ) ≥ f1( x ) , равна S = ∫(f2 ( x ) − f1( x ))dx . |
|||||
|
|
|
|
a |
|
|
|
Пример |
|
|
|
|
|
|
Найти |
площадь фигуры, |
ограниченной |
линиями |
||
y = −x2 , y = x − 2 . |
|
|
|
|
||
35
Решение
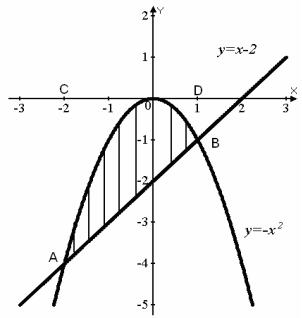
Изобразим кривые на чертеже (рис.4). Решив систему
y = −x2
y = x − 2 , получаем координаты двух точек пересе-
чения А (1; -1) и В (-2; -4). Искомую площадь S криволинейного треугольника можно представить как разность площадей двух криволинейных трапеций АСDB и AOB.
|
1 |
|
|
|
|
|
|
|
1 |
S = ∫( −x2 −( x − 2 ))dx = = ∫(−x2 − x + 2)dx = |
|||||||||
|
−2 |
|
|
|
|
|
|
|
−2 |
= (− |
x3 |
− |
x2 |
+ 2x) |
|
1 |
= |
9 |
= 4,5 . |
|
|||||||||
3 |
2 |
|
−2 |
2 |
|||||
|
|
|
|
|
|
|
|||
Рис. 4
36
4.Вычисление площадей плоских фигур в полярной системе координат
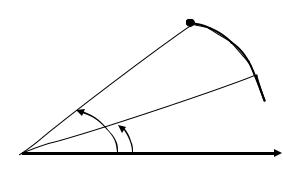
Фигура, ограниченная графиком функции (рис.5) r = r(ϕ ) и двумя лучами ϕ = α и ϕ = β , называется криво-
линейным сектором. Его площадь вычисляется по формуле
S = 1 ∫β r2 (ϕ )dϕ . 2 α
A r(ϕ)
ϕ=β
 B
B
ϕ=α
0 |
ρ |
Рис. 5
Если фигура имеет более сложную форму, то ее необходимо разбить лучами, выходящими из полюса, на криволинейные секторы. Может также встретиться фигура вида, изображенного на чертеже 6. В этом случае площадь фигуры может быть найдена как разность площадей двух криволинейных секторов ОАВ и ОСD по формуле
S = 1 ∫β (r12 (ϕ) − r22 (ϕ))dϕ . 2 α
37
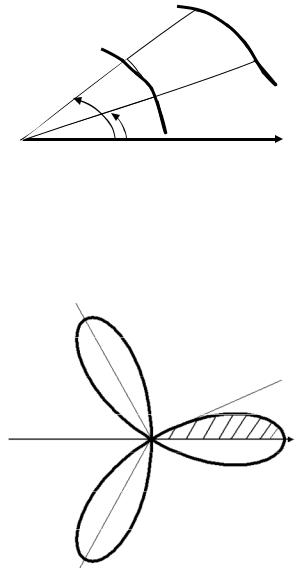
ϕ=β A r2(ϕ)
D B
r1(ϕ) C ϕ=α
|
0 |
|
|
ρ |
|
|
|
|
Рис. 6 |
||
Пример |
|
|
|
||
Найти площадь, |
ограниченную кривой r = 2 cos3ϕ |
||||
(рис. 7). |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
6 |
|
|
|
ρ |
0 |
|
|
|
|
|
|
|
|
Рис.7
38

Решение
Площади всех лепестков «трехлепестковой розы» равны, а каждый лепесток симметричен относительно своей оси, поэтому найдем площадь половины одного лепестка, умножим ее на 6 и получим площадь искомой фигуры:
|
|
|
π |
π |
|
S1 |
= |
1 |
∫6 |
( 2 cos 3ϕ )2 dϕ = 2∫6 |
1 + cos 6ϕ dϕ = |
|
|
2 |
0 |
0 |
2 |
ππ
= (ϕ |
6 |
+ |
sin 6ϕ 6 |
) = ( |
π |
+ 0) |
= |
π |
. |
||
0 |
6 |
0 |
6 |
6 |
|||||||
|
|
|
|
|
|
||||||
Тогда площадь всей фигуры равна
S= 6S1 = 6 π6 = π .
5.Вычисление длины дуги плоской кривой
Пусть в прямоугольной системе координат задана плоская кривая АВ уравнением y = f ( x ) , где a ≤ x ≤ b .
Если функция f ( x ) и ее производная непрерывны на отрезке [a;b], то длина кривой АВ может быть найдена по формуле
b
l = ∫ 1 + ( f x′(x))2 dx .
1 + ( f x′(x))2 dx .
a
Если линия задана уравнением x = ϕ( y ), c ≤ y ≤ d , то ее длина вычисляется по формуле
39
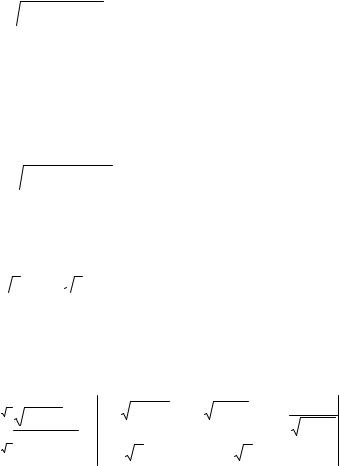
d
l = ∫ 1 + (ϕ′y ( y))2 dy .
1 + (ϕ′y ( y))2 dy .
|
c |
|
Если уравнение кривой АВ задано в параметрической |
||
форме |
x = x( t ) |
, t1 ≤ t ≤ t2 , причем x( t ), y( t ) – непрерыв- |
|
||
|
y = y( t ) |
|
ные функции с непрерывными производными и a = x(t1 ) , b = x(t2 ) , то длина кривой АВ находится по формуле
t2
l = ∫ (xt′)2 +( yt′)2 dt .
(xt′)2 +( yt′)2 dt .
t1
Примеры
1. Найти длину дуги кривой y = ln(2x) на промежутке
 3 ≤ x ≤
3 ≤ x ≤  8 .
8 .
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y′x |
= |
2 |
|
= |
1 |
|
+ ( y′x ) |
2 |
= |
1 + |
1 |
= |
1 + x2 |
|
|||||||||||||||||||
|
|
x |
, 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Тогда |
|
|||||||||||||||
|
2x |
|
|
|
|
x2 |
|
|
|
|
|
x2 |
|
tdt |
||||||||||||||||||||
|
l = ∫ |
1 |
+ x |
2 |
dx |
= t = 1 + x |
2 |
; x |
= t |
2 |
−1; dx = |
|||||||||||||||||||||||
|
|
|
t2 −1 = |
|||||||||||||||||||||||||||||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
x |
|
|
|
|
|
x = 3 |
t1 = 2; x |
= 8 t2 = 3 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
3 |
t2dt |
|
3 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
t −1 |
|
|
|
3 |
|
|
1 3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= ∫2 |
|
= |
∫2 (1 + |
|
)dt = t |
2 |
+ |
2 ln |
|
|
|
|
|
|
|
2 |
= |
1 + 2 ln |
|
. |
|
|||||||||||||
t2 −1 |
t2 −1 |
t +1 |
2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
40
