
pm_l_2 Прикл мех Сопромат
.pdf
61
|
|
|
|
|
|
|
|
|
b |
2 |
||
|
|
|
|
|
|
|
|
|
|
h |
||
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
2 |
|
|
|
y 2 |
|
|
|||
|
b |
|
|
|
4 |
|||||||
|
|
h |
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
ітоді |
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
y |
|
|
|
|
|
|
|||
2 |
4 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
y2 |
|
h |
|
2 |
|
|
6Q |
y |
|
||||
|
|
y 4 |
|
|
|
|
|
|
|
|
|
(12.7) |
|
|
|
|
|
|
|
|
|
bh3 |
|
|
|
||
|
|
|
|
|
|
|
Досліджуючи формулу (12.7) відмічаємо, що на поверхні
перерізуприy= h , дотичнанапругадорівнюєнулю, ауцентріваги
2
вона досягаємаксимальноївеличини(див. рис. 12.6,в) ідорівнює
|
|
h2 |
|
|
3 Qy |
3 |
|
Qy |
|
|||
|
6Qy |
4 |
|
|
(12.8) |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
max |
|
bh3 |
|
|
2 bh |
2 |
|
A |
|
|||
|
|
|
|
|
|
|||||||
12.5 Розрахунокнаміцністьпризгині
Досвідпоказує, що перевіркаміцностіпо дотичній напрузі виявляєтьсявирішальноютількидлядужекороткихівисокихбалок, а такождляматеріалів, якінедостатньочинятьопірсколюваннюітому розрахунокбалокведетьсяпонормальнимнапругаміумоваміцності призгинімаєвигляд:
|
|
M z max |
, |
(12.9) |
|
||||
max |
|
Wz |
|
|
|
|
|
||
деMz max – максимальназгинаючанапруга, взятаізепюриMz , [ ] – припустиманапругапризгині, якадорівнюєприпустимійнапрузіпри розтягу. Із умови міцностіможна визначити потрібний осьовий моментопорубалки
W |
Mz max |
, |
(12.10) |
|
|||
z |
|
|
|
|
|
||
Співвідношення (12.10) дозволяє приймати раціональну форму поперечногоперерізубалки, тобтоприйматитуформуперерізу, яка маєбільшийWz приоднаковійплощі.
Увипадку, колинеобхідноврахуватиідотичнунапругу, умова міцностімаєвигляд:
2 |
2 |
|
|
|
4 |
|
|
||
max |
|
|
(12.11) |
|
|
|
|||
2 |
|
|
|
|
62
У формулу(12.11) підставляютьзначення іτдлявідповідного перерізубалки.
12.6 Деформаціїпризгині
Стержні, якізастосовуютьсявінженернихспорудах, повинні володіти не тільки визначеною міцністю, але і достатньою жорсткістю.
Під розрахунком на жорсткість розуміють оцінку пружної піддатливостібалкипіддією прикладеногонавантаженнятадобір такихрозмірівпоперечногоперерізу, приякихпереміщеннянебуде перевищувативстановленихнормамиграниць. Длявиконаннятакого розрахункутребанавчитисьобчислюватипереміщенняточокбалки піддієюбудь-якихзовнішніхнавантажень. Розглядаючидеформацію балкиприплоскомузгині, можнавідмітити, щовісьбалкипіддією навантаженняводнійзголовнихплощинінерціївикривлюєтьсявтій самійплощині, апоперечніперерізиповертаютьсяіводночасдістають поступальнепереміщеннявнапряміосіу. Викривленувісьбалки називаютьзігнутоювіссюабопружною лінією. Переміщенняцентру вагиперерізувнапрямі, перпендикулярномудонедеформованоїосі балки, називаєтьсяпрогиномбалкивданомуперерізійпозначається літероюу, анайбільшийпрогинбалкиназиваєтьсястрілоюпрогинуі позначаєтьсялітерою f. Кутθ, наякийкожнийперерізповертається відносносвогопочатковогоположення, називаєтьсякутомповороту перерізуівінвизначаєтьсязаформулою
x |
dy( x ) |
y , |
(12.12) |
|
|||
|
dx |
|
|
Припустиміпрогини такути повороту перерізів встановлюються нормами.
Визначимо диференційне рівняння пружної лінії балки. Враховуючи, щоміжкривизноюізгинаючиммоментоміснуєзв’язок
K |
1 |
|
M z |
, |
(12.13) |
|
|
||||
|
EIz |
|
|
||
деρ– радіускривизни, іякщобалкапостійногоперерізутавідчуває “чистий”згин, томожназаписати
Mz |
const . |
(12.14) |
|
||
EI z |
|
|
- 1
Отже, ρ=const іρ=const, цевказуєнате, щовісьбалкидеформується поколу. Слідвідмітити, щовзагальномувипадкубезпосередньо застосовуватизаконвизначеннякривизнидляобчисленняпрогинівне
63
вдається. Дляаналітичногорозв’язанняцієїзадачівикористовується значеннякривизни(дивиськурсматематики):
|
|
|
|
|
|
|
|
|
d 2 y |
|
|
|
|
|
|
||
K |
1 |
|
|
|
|
|
dx2 |
|
|
|
|
|
(12.15) |
||||
|
|
|
|
|
2 |
|
3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
dy |
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Підставивши в (12.13) |
|
|
|
|
|
|
|
|
дістаємо |
||||||||
|
значення кривизни із (12.15) |
||||||||||||||||
диференційнерівнянняосізігнутоїбалки |
|
||||||||||||||||
|
|
|
d 2 y |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
dx2 |
|
|
|
|
M z |
|
(12.16) |
|||||||
|
|
|
|
|
|
|
|
3 |
EIz |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
dy |
|
2 2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Інтегруванняцьогорівнянняпов’язанозвеликимитруднощами |
|||||||||||||||||
(вононелінійнеінеодноріднедругогопорядку), алевраховуючи, що напрактицімаємосправузмалимипрогинами(ymax<(0,002…0,003)l) тодітангенсикутівнахилу(dy/dx) дотичноїдоосібудутьмаліітому квадратом першоїпохідноїузнаменнику(dy/dx)2 упорівнянніз
одиницею можливо знехтувати ітому рівняння (12.16) |
приймає |
|||||
вигляд: |
|
|
|
|
||
|
d 2 y |
|
|
Mz |
|
(12.17) |
|
dx2 |
EI z |
||||
|
|
|
||||
Рівняння(12.17) |
єнаближеним диференційнимрівняннямосі |
|||||
зігнутоїбалки. Двазнакиурівнянні(12.17) поставленітому, щознак кривизниможенеспівпадатиіззнаком згинаючогомоменту. Для визначеннязнаківможнаскористатисятакою умовою. Якщовісьу направленаугору, тоурівнянні(12.17) беретьсязнак“плюс”, аякщо униз, то- “мінус”.
Для того, щоб отримати аналітичний вираздля прогинів, необхіднознайтирішеннядорівняння(12.17). Правачастинацього рівнянняєвідомоюфункцієювідх, тому, інтегруючирівняння(12.17) першийраз, отримуємо:
dy |
|
M z |
dx C , |
(12.18) |
dx EIz
64
деdy/dx – цекутповоротуперерізу. Інтегруючидругийразрівняння (12.17) дістаємопрогин:
y |
M z |
dx2 CX D |
(12.19) |
EIz
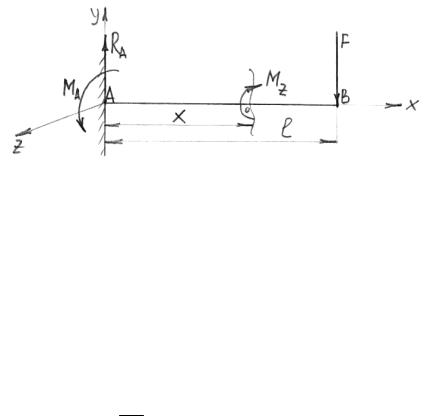
ПостійнівеличиниінтегруванняC іD знаходимо, використовуючи граничні умови, які залежать від способу закріплення балки. Розглянемоприкладвизначенняпрогинудляконсольноїбалки(див. рис. 12.7). ДлявизначеннязгинаючогомоментуМz розглядаємоправу частинубалкиі, отже:
|
|
|
|
|
|
|
|
Рисунок12.7 – Визначенняпрогину |
|
|
|
|||||||||||||||
Mz |
F( l x ) F( x l ) , де0 x l, ітодімаємо: |
|||||||||||||||||||||||||
d 2y |
|
|
|
M z |
|
|
F x l |
ідалі |
dy |
|
|
F |
|
( x l )dx C |
||||||||||||
dx2 |
|
|
|
|
EIz |
|
|
|
EI z |
|
dx |
|
EI z |
|
||||||||||||
|
F |
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
( |
|
|
|
lx ) C , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
EIz |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
F |
|
|
|
|
|
|
x 2 |
|
|
|
|
F |
|
x 3 |
|
lx 2 |
||||||
y |
|
|
|
|
|
( |
|
|
|
lx C )dx D |
|
|
|
( |
|
|
|
|
) Cx D . |
|||||||
EIz |
|
|
|
|
|
EIz |
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
6 |
2 |
|
||||||||||||
Оскількиграничніумовидлябалки(див. рис. 12.7) yA=yA =0, тоді
0 F ( 0 0 ) C ізвідсиC=0,
EI z

65
0 F (0 0) 0 D іD=0,
EI z
ітакимчиноммаєморівнянняпружноїлініїрозглядаємоїбалки
|
|
|
|
|
|
|
|
|
F |
|
|
|
x3 |
lx 2 |
|
|
|
|
|||||||
|
|
|
|
|
y |
|
|
( |
|
|
|
|
|
|
|
|
|
) . |
|
|
|
|
|||
|
|
|
|
|
EIz |
6 |
|
|
|
2 |
|
|
|
|
|
||||||||||
Визначаємомаксимальнийпрогинбалки. |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
F |
|
|
|
l |
|
l |
|
|
|
|
Fl |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, знак“мінус”вказуєна |
||||
y |
max |
y |
B |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x l |
|
|
|
EIz |
|
2 |
|
3EI z |
||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
6 |
|
|||||||||||||||
те, щонапрямокпрогинунеспівпадаєзпозитивнимнапрямкомосіу. Визначення переміщень в балках методом безпосереднього
інтегруваннядиференціального рівнянняпружноїлініїувипадку балок з великою кількістю ділянок пов’язано із значними труднощами. Томудлязменшеннявеликоїобчислювальноїроботи, пов’язаної з визначенням сталих інтегрування, останнім часом розробленодекількаметодів.
Донихупершучергуналежитьметодпочатковихпараметрів, котрийдаєзмогуприбудь-якійкількостіділянокзвестирозв’язання довідшуканнявсьогодвохсталих прогинуікутаповоротуна початку координат. Для того, щоб користуватися цим методом, необхіднодотримуватисянаступнихумов:
1.Відрахунокгоризонтальнихкоординатусіхділянокповинен бутивідодногопочаткукоординат, тобтокрайньоїлівоїабокрайньої правоїточкиосібалки.
2.Всі нововведеніскладові виразу згинаючого моменту наступнихділянокповинніміститиусобімножникдужки(x–l0), деl0
–сумадовжинусіхпопередніхділянокдовідповідногонавантаження.
3.При розрахункузгинаючихмоментівтребарозглядатиту частинубалки, якаміститьпочатоккоординат.
4.Інтегруваннядиференційного рівнянняповинно бути без розкриттядужки(x–l0).
5.Розподілененавантаженнянеповинноперериватись, але якщовонопереривається, тойогослідпродовжитидокінцябалки, і додавшиприцьому(відперерізу, девонопереривається) розподілене навантаженнятієїжінтенсивності, алепротилежногознаку.
66
6. У формулідлявизначеннядеформаційпризгинівводятьті навантаження, якірозміщенівідпочаткукоординатдоперерізу, в якомувизначаєтьсявідповіднадеформація.
Формулидлявизначеннякутаповоротуіпрогинупризгині балокмаютьвигляд
EI EI |
|
M ( x l0 |
) |
|
F( x l0 )2 |
|
q( x l0 )3 |
i |
|||||||
|
|
|
|
|
|
||||||||||
0 |
1! |
|
|
|
2! |
|
|
3! |
|
||||||
EIy EIy |
EI x |
M ( x l0 )2 |
|
F( x l0 )3 |
|
|
|||||||||
|
|
|
|||||||||||||
0 |
|
0 |
|
|
2! |
|
|
3! |
|
|
|
||||
|
|
|
|
) 4 |
|
|
|
|
|
|
|
||||
|
q( x l |
|
|
|
|
|
|
|
|
|
|
||||
|
4! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
, |
|
|
|
|
|
|
|
|
|
(12.20) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
де l0 – горизонтальна координата від початку координат до відповідного навантаження, Θ0 іу0 – відповідніхарактеристики деформаціїуперерізіприх=0, тобтоупочаткукоординат. Якщо початоккоординатбуденалівомукінцібалки, тозгинаючиймомент будепозитивним, якщовінмаєнапрямокзарухом годинникової стрілкиісилаірозподілененавантаженнябудутьпозитивні, якщо вонимаютьнапрямокугору. Якщопочатоккоординатнаправому кінцібалки, тознакиунавантаженьбудутьпротилежними.
Визначаємомаксимальнийпрогиндлябалки(див. рис. 12.7) за методомпочатковихпараметрів.
Оскількипочатоккоординатналівомукінцібалки, топотрібно спочатку визначити реакціїопори А, для цього складаємо два рівняннярівноваги:
1.ΣFky=0, RA–F=0 іRA=F
2.ΣmA=0, –MA+Fl=0 іMA=Fl
Використовуючиформулу(12.20), маємо:
EIy EIy |
EIy x |
|
M( x l0 )2 |
|
F ( x l0 )3 |
|
|
|
q( x l0 )4 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
0 |
|
0 |
|
2! |
|
|
|
|
|
|
3! |
|
|
|
|
4! |
|
|
|
||||||||||
ітакякy =y =0, |
y |
'= = y '=0 |
ідоперерізуВдіютьтількиR |
i M , |
|||||||||||||||||||||||||
0 |
A |
0 |
0 |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
A |
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M A x2 |
|
RAx3 |
|
|
Flx2 |
|
Fx3 |
|
|
|
|
|
|
|
|
|||||||||||
|
EIy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Звідси |
|
|
2 |
|
|
|
6 |
|
|
|
2 |
|
6 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fl l2 |
|
|
Fl3 |
|
|
Fl3 |
|
|
|
|
|
Fl3 |
||||||||
|
EIyB EI y |
x l |
|
|
|
|
|
|
|
|
|
|
|
і yB |
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
2 |
|
6 |
|
3 |
|
|
|
|
|
3EI |
||||||||||||
67
68
ЛЕКЦІЯ17
13 СКЛАДНИЙОПІРТАСТІЙКІСТЬСТИСНЕНИХ СТЕРЖНІВ
Підскладнимопоромрозуміютьрізнікомбінаціїпростих(плоских) напруженихстанівстержня(розтягу, стиску, кручення, згину).
В загальному випадку навантаження стержня в поперечних перерізахможутьдіятишістьвнутрішніхсиловихчинників-Nx, Qy, Qz, Mk, My іMz. Напруженийстанприцьомузнаходятьнаосновіпринципу суперпозиції. Згідно з даним принципом, у досліджуваній точці розраховуютьокремонапругивіддіїкожногосиловогочинника, після чогоїхпідсумовуютьівизначаютьсумарнікомпонентинапруг. Зрозуміло, щознаючинапруженийстануточціівикористовуючитучиіншутеорію міцності, можнапровестирозрахункинаміцністьданогоелемента.
Напрактиціодночаснодіявсіхсиловихчинниківзустрічається рідко. Частішеприходитьсяматисправузрізнимиїхкомбінаціями, якімиі розглянемо.
13.1 Косийзгин
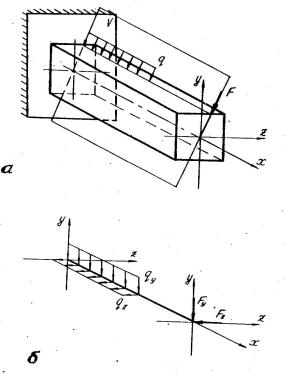
Косим називаютьзгин, заякогоплощинадіїнавантаженьне збігаєтьсязжодноюізголовнихосейперерізу. Наприклад, нарис.13.1, а силаF ірозподілененавантаженняq діютьуплощиніV, яканезбігаєтьсяз головнимиплощинамиxy i xz. Підчасрозрахунківкожнеізнавантажень розкладаютьнаскладовічастини, що діють у головних площинах (рис.13.1,б). Отжекосийзгинрозглядаютьяксумудвохплоскихзгиніву двохвзаємноперпендикулярнихплощинах.
Розглянемоконсольнубалкудовжиною l прямокутногоперерізу (рис.13.2), докінцяякоїприкладеносилуF, щоутворюєзвіссюукутα. РозкладемосилуF надвіскладові, напрямленівздовж головнихосей перерізу:
Fy=Fcosα, Fz=Fsinα
(13.1)
69
У поперечнихперерізахбалкисилиFy, Fz утворюютьчотири(із шести) внутрішніхсиловихчинників: Qy , Qz , My іMz. Урозрахункахна міцність, якізаплоскогозгину, нехтуютьсиламиQy, Qz іутворюваними ними дотичними напругами. Тодізначення згинаючих моментів у довільномупоперечномуперерізібалки, взятомунавідстаніхвідкінця консолі, будуть
Рисунок13.1 - Неплоскийзгин(а) ісхематичнезображенняйогоувиглядідвохплоских(б)
Mz = Fyx, My =Fzx (13.2)
Згинаючий момент вважають додатним, якщо в першому квадрантіперерізувінрозтягуєволокнабалки, івід’ємним, якщо утворюєстискволокон. УрозглядуваномуприкладіMy іMz – додатні.
ЕпюризгинаючихмоментівMy іMz зображенінарис. 13.3.
70
