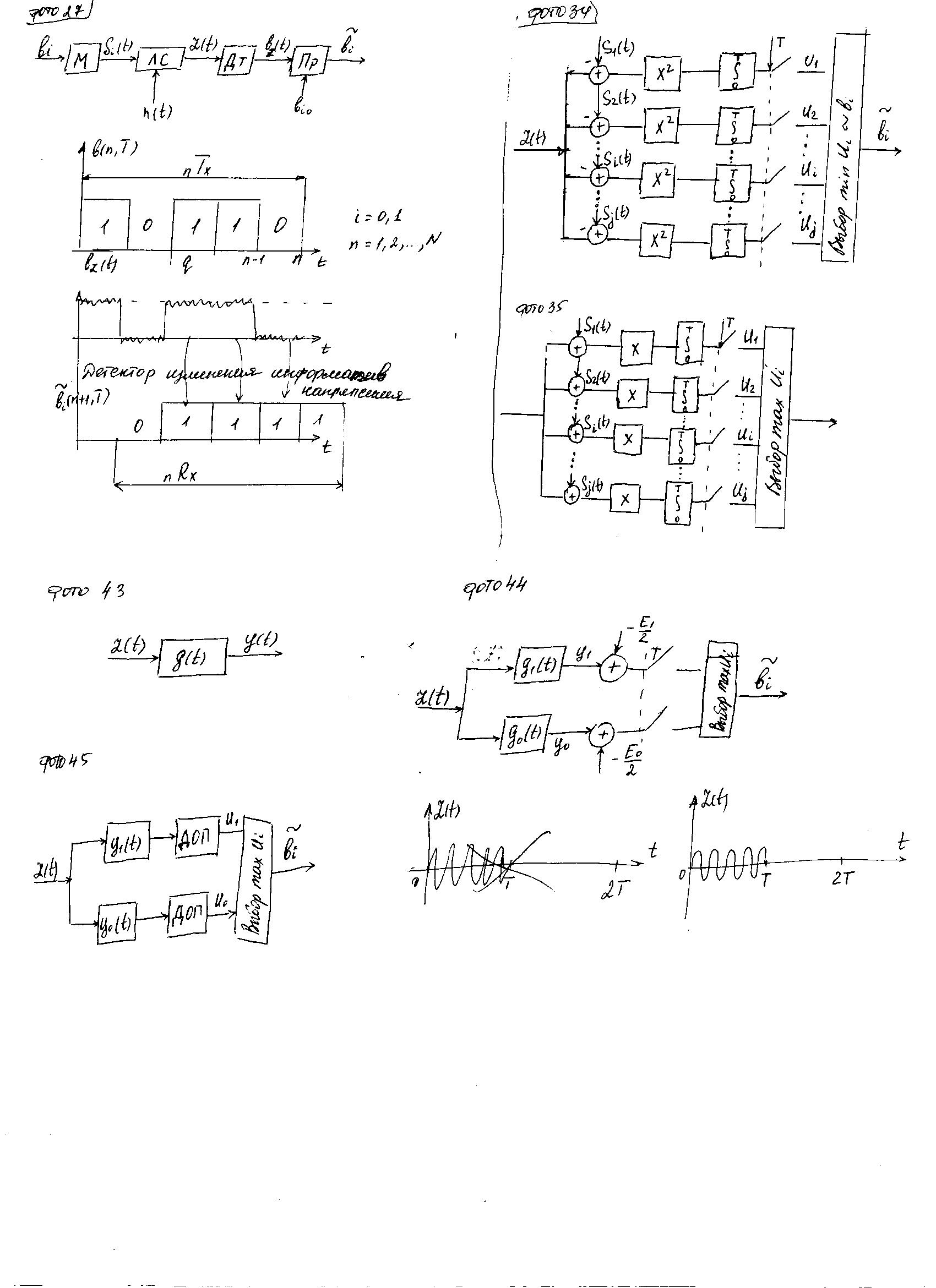
30.Оптимальные алгоритмы приема при полностью известных сигналах. Оптимальный приемник на «вычитателях».

Оптимальный поиск экстремума, т.е. max или min некоторого критерия, обеспечивающего наименьшую вероятность ошибки, наибольшее отношение правдоподобия Существуют ограничения диапазона изменения параметра (физические огранич-я, экономические, критерий физической осуществимости).Математическая постановка задачи: Оптимальный приемник – приемник, который обеспечивает минимальные критерии.

Он получает сигнал из линии, на выходе- . - информационная составляющая с помехами(ограниченный ГБШ). Посылки, кот. подаются в ЛС имеют длительность Т; n(t)~N₀ ;

,

m – количество отсчетов, кот. можно сделать за интервал Т.

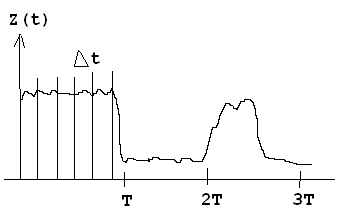-СПМ для шума- дисперсия шумов;

Рассмотрим КС в кот. передаются только активные сигналы(т е нет пассивной паузы) . ,

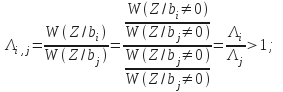
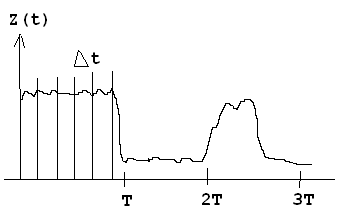
31.Оптимальные алгоритмы приема при полностью известных сигналах. Оптимальный приемник на корреляторах

Оптимальный поиск экстремума, т.е. max или min некоторого критерия, обеспечивающего наименьшую вероятность ошибки, наибольшее отношение правдоподобия Существуют ограничения диапазона изменения параметра (физические огранич-я, экономические, критерий физической осуществимости).Математическая постановка задачи: Оптимальный приемник – приемник, который обеспечивает минимальные критерии.

Он получает сигнал из линии, на выходе- . - информационная составляющая с помехами(ограниченный ГБШ). Посылки, кот. подаются в ЛС имеют длительность Т; n(t)~N₀ ;

,

m – количество отсчетов, кот. можно сделать за интервал Т.

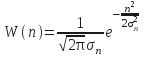
-СПМ для шума- дисперсия шумов;

Структура с корреляторами («коррелировать» означает совпадать)

- правило построения оптимального приемника.

Такая система минимизирует вероятность ошибки (идеально помехоустойчива). Корреляторы пытаются найти соответствие принятого

сигнала Z(t) с каждым возможным сигналом прототипом S_i(t), известным приемнику априори.

Структурная схема приемника, реализующего оптимальный алгоритм приема, имеет следующий вид:

31.оборот

Тот канал, который обеспечит наибольший корреляционный интеграл обеспечит max U_i . Т.е. разумное правило принятия решения звучит так:

выбрать сигнал S_i(t), который лучше всего согласовывается с сигналом Z(t).

Приемник должен быть когерентным. Ключи должны замыкаться одновременно, когда процесс накопления энергии закончится.

Существует оптимальная процедура приема, к-я позволяет получить минимальную вероятность ошибки.

30-Б.Пот.Пом.При изв.Наб.Сиг.Пост.З-чи и получ.Выр-я для вер.Ош. Приема.

Речь идет о когерентном приеме. Известна частота и фаза сигнала

Для бинарного канала связи i~”1”; j~”0.

условие выдачи «1», в противном случае демодулятор выдает «0».

, Ошибка – пропуск сигнала ~ ; определяется условием

Вероятность связывается с решением, определяемым неравенством

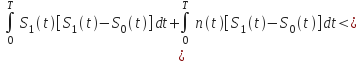
или вероятность связывается с другим

Для получим аналогичное соотношение. Ошибка – ложная тревога , т.к..

Обозначим

эквивалентная

30-оборот

Правило решения дает алгоритм приемного устройства

,(*)

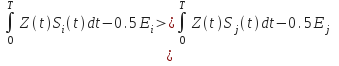
Из пришедшегосигнала вычитает альтернативный, разница – ГБШ. Мощность этих шумов минимальна. Сигнал, переданный в ЛС потерялся.

29-обот 2. ;

;

-

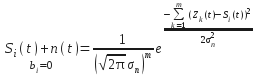- m мерный дифференциальный закон распределения.

Критерий отношения распределения

Отношение правдоподобия для сигнала :

, где ; Прологарифмировав экспоненту получим

;

сделаем предельный переход

30-б оборот энергия сигнала.

Неравенства, соответствующие ошибочным решениям будут иметь вид: ,нормально распределенная величина (случайная) с МО=0; и дисперсией:

коррел.ф-цииГБШ (N₀ - СПМГБШ). Тогда

;Вероятность ошибки будет равна

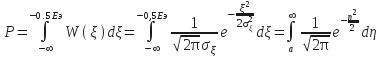Где ;

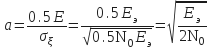
Воспользовавшись табулированной формулой Крампа

получим