2.1.5 Розрахунки на міцність за допустимими напруженнями

При розрахунках за допустимими напруженнями міцність конструкції або її елементів буде забезпечена, якщо максимальне напруження _max не перевищує допустимого, тобто виконується умова

. (2.12)

Якщо матеріал по різному чинить опір розтяганню і стисканню (характерно для крихких матеріалів), то найбільші розтягувальні напруження не повинні перевищувати допустимих напружень на розтягання []_р , а найбільші стискувальні напруження  допустимих напружень на стискання []_с. Формула (2.12) дає можливість розв’язувати низку інженерних задач.

Проектний розрахунок – підбір перерізу елементу конструкції при відомих силах, що діють на елемент

. (2.13)

Перевірний розрахунок, при якому визначають напруження і порівнюють його з допустимим

. (2.14)

При перевірному розрахунку, як правило, визначають коефіцієнт запасу міцності, з яким працює елемент.

Визначення допустимого навантаження на існуючий елемент

. (2.15)

Умови міцності вимагають, щоб напруження, які виникають в елементах конструкцій, не перевищували допустимих. Допустимі напруження [] становлять деяку частину від небезпечних напружень. Для пластичних матеріалів таким небезпечним напруженням є границя текучості _т , при якій деформації, що швидко зростають, перешкоджають нормальній експлуатації конструкції. Для крихких матеріалів небезпечним напруженням є границя міцності _в , при якій настає руйнування матеріалу. Допустиме напруження визначають за формулою

, (2.20)

де _н = _т  для пластичних матеріалів і _н = _в  для крихких, n  коефіцієнт запасу міцності при дії на конструкцію статичного навантаження встановлюється в межах n = 1,5...2, для крихких  n = 3...5, а іноді і вище (наприклад, для каменів природних і штучних він може бути в межах n = 10...30). Коефіцієнт запасу міцності залежить також від умов роботи конструкції, точності розрахунків напружень, характеру навантажень.

2.2 Завдання до розрахунково-графічної роботи

Задача 2. Розрахунок статично невизначуваних систем при розтягу (стиску) із пружними зв’язками

Абсолютно жорстка балка піддержується в горизонтальному положенні пружними стальними стержнями згідно схеми (рис. 2.3 – 2.6). Обчислити необхідну площу перерізів цих стержнів при заданому їх співвідношенні.

Матеріали стержнів та співвідношення площ вказані на рисунку. Інші дані для розрахунку взяти з таблиці.

Таблиця 2.1

Варіант	Р1, кН	а, см
0	10	90
1	12	85
2	14	80
3	16	75
4	18	70
5	20	65
6	22	60
7	24	55
8	25	70
9	11	50

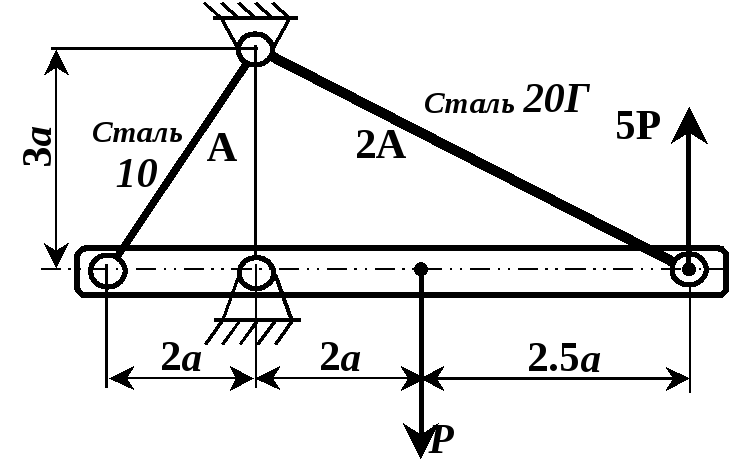
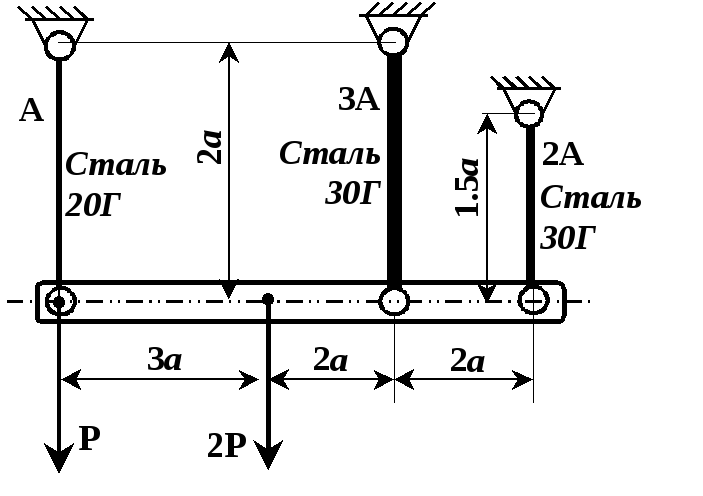
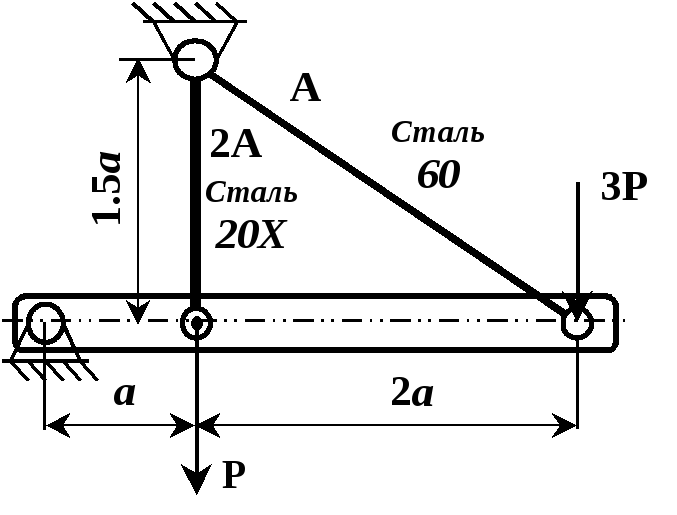
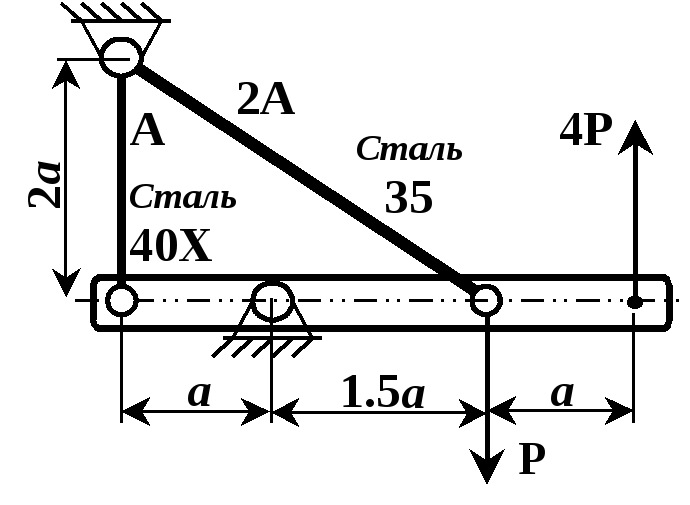
Рисунок 2.3

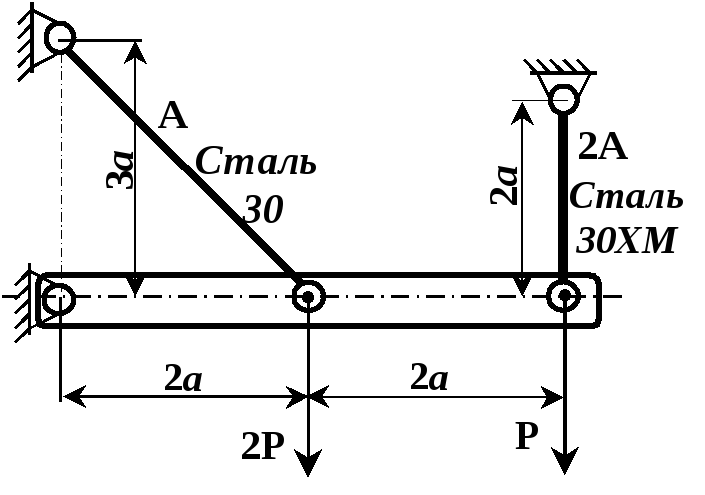
Рисунок 2.4

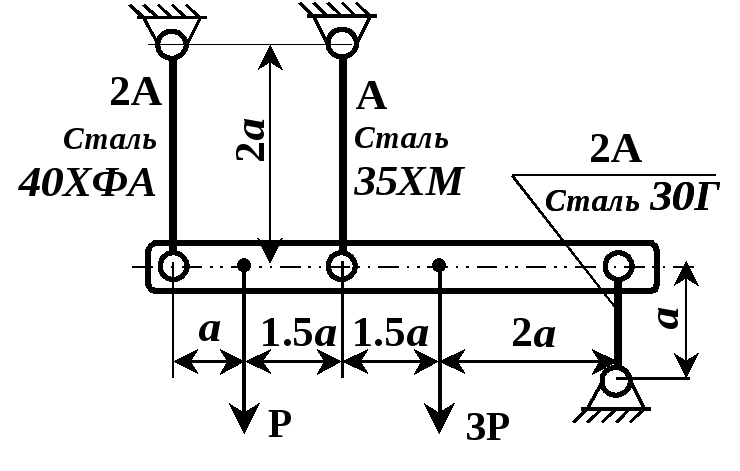
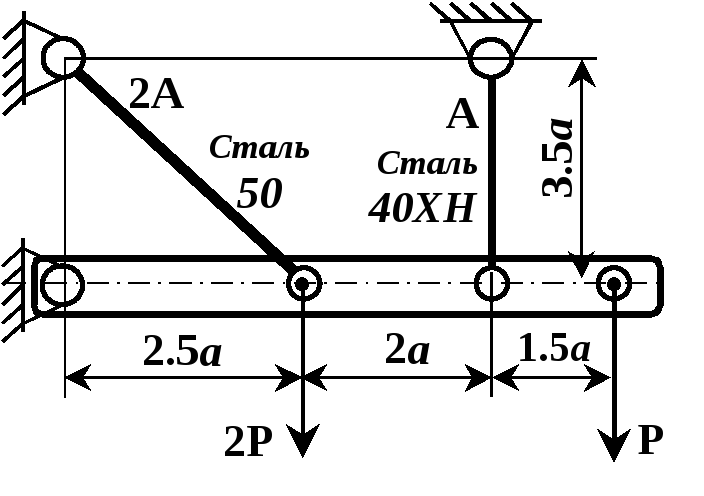
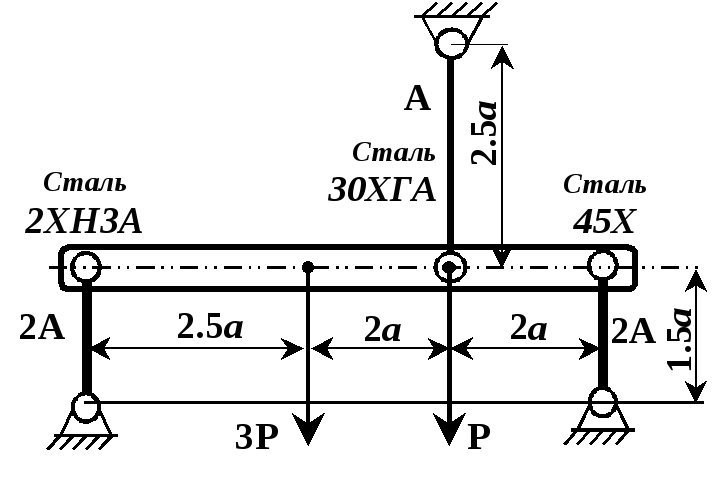
Рисунок 2.5

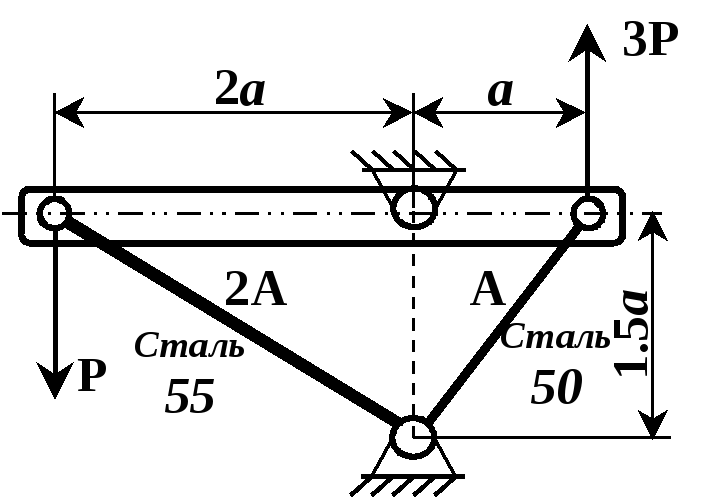
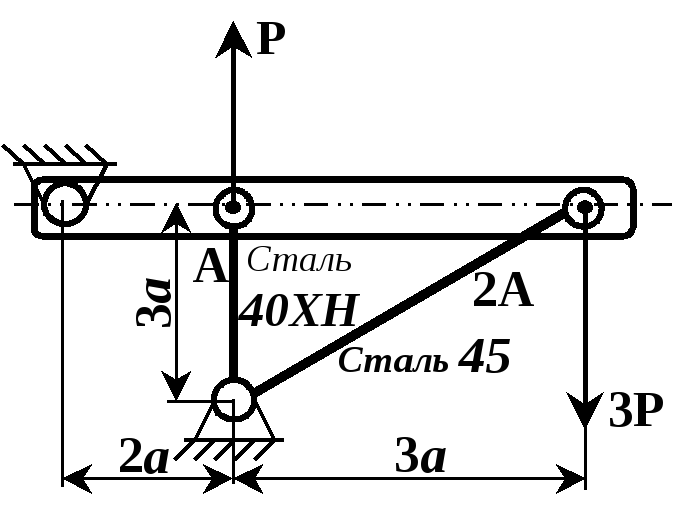
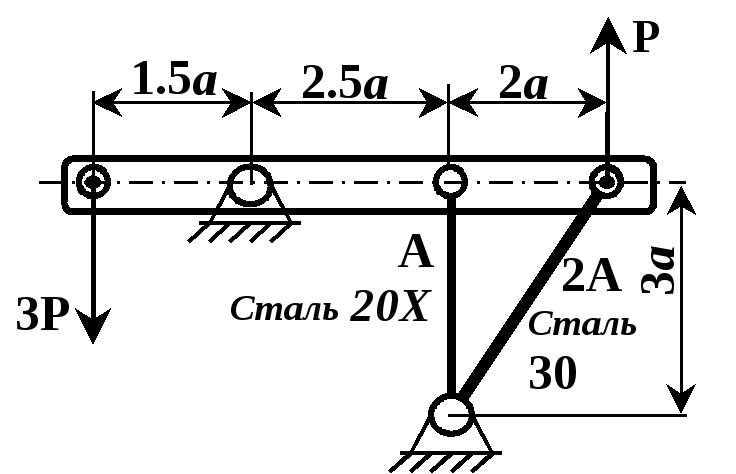
Рисунок 2.6

Приклад А. Жорстка балка підтримується двома стержнями, як показано на рисунку 2.7. Перший стержень повинен мати площу поперечного перерізу в два рази більшу ніж другий; матеріал стержнів – сталь 30Г. Визначити площу поперечного перерізу стержнів.

Дано: а=1 м; b=2 м; с=1,5 м; =45^; Р=120 кН; А₁=2А₂; Е₁=Е₂=Е.

Визначити: А₁?; А₂?

Розв’язування. В задачі потрібно визначити площі перерізів стержнів, тобто провести проектний розрахунок. Оскільки стержні системи працюють на розтяганнястискання, то проектний розрахунок виконується за формулою (2.13), а розв’язування задачі зводиться до визначення нормальних сил в поперечних перерізах стержнів 1 і 2.

Статична сторона задачі

В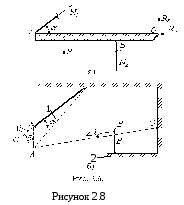икористаємо метод перерізів і переріжемо стержні поперечними перерізами, відкинемо верхню частину стержня 1 і нижню частину стержня 2, замінимо їх дію нормальними силамиN₁ та N₂. Використовуючи формальний підхід, припустимо, що обидва стержні розтягнуті, тобто направимо N₁ та N₂ від перерізів. Відкинемо також шарнір і замінимо реакціями R_x та R_y (рисунок 2.8, а).

Для визначення чотирьох невідомих реакцій N₁ ,N₂ ,R_x ,R_y ми можемо скласти лише 3 незалежних рівняння статики, як для плоскої непаралельної системи сил, тобто

Отже, система один раз статично невизначувана.

Перші два рівняння статики крім N₁ та N₂ містять невідомі реакції R_x та R_y, визначати які немає необхідності. Отже, відносно невідомих зусиль N₁ та N₂ ми маємо лише одне рівняння:

. (2.21)

Рівняння (2.21) містить дві невідомих величини. Для однозначного розв’язання задачі необхідно знайти ще одне рівняння, що пов’язує N₁ та N₂. Для цього необхідно скласти рівняння сумісності переміщень.

Геометрична сторона задачі

Розглянемо систему в деформованому стані.

За умовою задачі балка абсолютно жорстка, стержні 1 та 2 – пружні. Нехай стержень 1 в результаті дії зовнішніх сил на систему видовжиться на величину l₁.

Методом засічок визначимо положення балки ОВ’А’, яке відповідає цьому видовженню (див рис. 2.8, б). Тоді стержень 2 набуде деформації стиску величиною -l₂, тобто ВВ’ = l₂.

Примітка. Балка закріплена в точці О шарнірно-нерухомою опорою, тому вона може повернутись тільки за або проти годинникової стрілки відносно точки О. Кут повороту балки нескінченно малий, тому вважається, що точки А та В в процесі деформації системи рухаються по вертикалі, катет АС в прямокутному трикутнику АСА’ відповідає геометрично величині l₁, а кут при вершині А’ дорівнюватиме куту  (див. рис. 2.8).

Із трикутника АСА’ маємо АС =l₁,

АА’ = АС/ sin 45^o = l₁/sin 45^o. (2.22)

Із подібності трикутників  ОВВ’   ОАА’ випливає

,

АА’=3ВВ’,

де ВВ’ = l₂.

З врахуванням (2.22) отримаємо рівняння сумісності переміщень

. (2.23)

Фізична сторона задачі

Виразимо l₁ та l₂ через зусилля в стержнях N₁ та N₂ у відповідності до закону Гука (2.9)

Враховуючи, що А₁=2А₂, підставимо вирази для

l₁ та l₂ в рівняння (2.23)

,

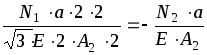N₁= 3N_2. (2.25)

Сумісним розв’язуванням рівнянь (2.21) та (2.25) визначаємо N₁ та N₂

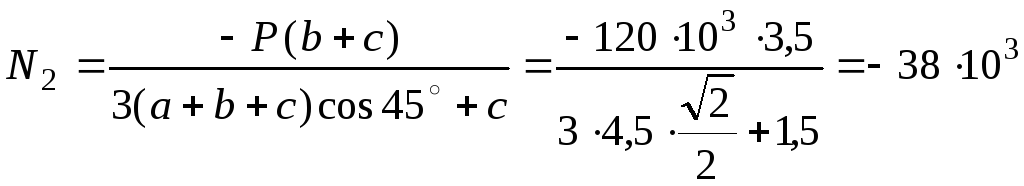Н,

N₁ = 3N₂ = 11410³ Н.

Отримані знаки зусиль говорять про те, що при навантаженні системи силою Р стержень 1 розтягується, а стержень 2 стискається. Порівняння величин N₁ та N₂ показує, що перший стержень більш навантажений.

Проектний розрахунок стержнів

Визначаємо допустимі напруження. Допустиме напруження для сталі 30Г (пластичний матеріал) дорівнює (формула 2.20)

= 160 МПа,

де _н = _т = 320 МПа  границя текучості сталі 30Г (див. додаток Ж),

n  коефіцієнт запасу міцності при дії на конструкцію статичного навантаження n = 1,5...2, приймаємо n = 2.

Таким чином = 160 МПа.

Визначаємо необхідні площі А₁, А₁

м² = 7,12 см², (2.26)

м² = 2,38 см². (2.27)

За умовою задачі має виконуватись співвідношення А₁ = 2А₂. Нехай А₁ = S, тоді

А₂ = S/2  2,38, (з нерівності 2.27),

звідки S  4,76 см²,

А₁ = S  7,12 см², (з нерівності 2.26).

Остаточно приймаємо S = А₁ = 7,2 см², тоді см².

Розрахуємо робочі напруження в стержнях

Н/м² =158 МПа< []=160 МПа,

стержень 1 буде працювати із коефіцієнтом запасу = 2,03.

Н/м² = 105,5 МПа< [] = 160 МПа.

стержень 2 буде працювати із коефіцієнтом запасу = 3,03.

Таким чином, стержень 2 буде недовантажений при прийнятому коефіцієнті запасу, що є нераціонально з точки зору економії матеріалу. Але надійність та жорсткість конструкції в цілому неодмінно збільшиться.

Відповідь: А₁ = 7,2 см², А₂ = 3,6 см².

П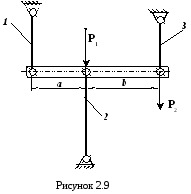риклад Б. Скласти рівняння сумісності деформацій для статично невизначуваної системи, приведеної на рис. 2.9. а = 1 м, b = 2 м.

Розв’язування.

Система, показана на рис. 2.9 один раз статично невизначувана. На балку діють зовнішні сили Р₁ та Р₂ та сили реакцій стержнів N₁, N₂ та N₃. Балка знаходиться під дією системи плоскопаралельних сил, тому статична сторона задачі вичерпується записом двох рівнянь, наприклад

Отже, необхідно скласти лише одне рівняння сумісності деформацій.

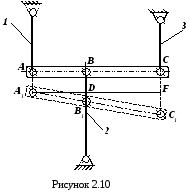
Розглянемо систему в деформованому стані, що відповідає кінематично можливому переміщенню (рис. 2.10).

За умовою задачі балка абсолютно жорстка, стержні 1, 2 та 3 – пружні. Нехай стержень 1 в результаті дії зовнішніх сил на систему видовжиться на величину l₁, а стержень 3 – видовжиться на величину l₃.

Методом засічок визначимо положення балки ОВ₁А₁, яке відповідає цьому видовженню (див рис. 2.8, б). Тоді стержень 2 набуде деформації стиску величиною -l₂, тобто ВВ₁ = l₂.

Примітка.Кінематично можливе переміщення балки складається із двох переміщень: балка може опуститись (піднятись) на деяку відстань та повернутись на певний кут. Обидва переміщення можна вважати нескінченно малими в порівнянні із вихідними розмірами стержнів та балки. Тому вважається, що точки А, В та С в процесі деформації системи рухаються по вертикалі.

Опустимо перпендикуляр із точки А₁ на відрізок СС₁. В результаті побудови отримаємо два прямокутні трикутники  А₁DВ₁ та  А₁FC₁.

Із подібності трикутників  А₁DВ₁   А₁FC₁ випливає

. (2.28)

Виражаємо катети трикутників через фізичні величини, якім вони відповідають

DВ₁ = ВВ₁ – BD = ВВ₁ – AA₁= l₂ – l₁,

FC₁ = CC₁ – CF = CC₁ – AA₁= l₃ – l₁,

де AA₁ = l₁, ВВ₁ = –l₂, CC₁ = l₃.

З врахуванням (2.28) отримаємо рівняння сумісності переміщень

,

остаточно маємо

. (2.29)

Відповідь: .