Оценка погрешности и определение порядка точности для формулы трапеций

Оценим погрешность приближенного значения интеграла, получаемого по формулам трапеций (необобщенной и обобщенной) и найдем порядки точности этих формул. При этом будем предполагать, что подынтегральная функция имеет непрерывную (и следовательно, ограниченную) вторую производную на отрезке.

Оценка погрешности необобщенной формулы трапеций. Оценим сверху модуль разности между точным и приближенным значениями интеграла, получаемыми с помощью необобщенной формулы трапеций (абсолютную погрешность приближенного значения интеграла), и получим оценку погрешности необобщенной формулы трапеций:

. (8.1.21)

В процессе преобразований использована формула (8.1.10), свойства определенного интеграла, формула (4.1.15) при ,,, а также то, чтона отрезке. Здесь мажорантная оценка модуля второй производной подынтегральной функции на отрезке (на отрезке .

Определение порядка точности необобщенной формулы трапеций. Введем обозначения, и разложим разность между точным и приближенным значениями интеграла, вычисленным с помощью необобщенной формулы трапеций, по степеням h:

. (8.1.22)

Для этого запишем разложение функции по формуле Тейлора с центром в точкеи остаточным членом в форме Пеано:

при . (8.1.23)

Запишем это разложение при и при:

при , (8.1.24)

при . (8.1.25)

Подставим разложения (8.1.23) – (8.1.25) в (8.1.22):

. (8.1.26)

Докажем, что если при, топри. В самом деле, первое утверждение означает, что

при . (8.1.27)

Рассмотрим отношение интегралов:

при ,

что и требовалось доказать. Здесь и первообразные функций и. Для вычисления интегралов использована формула Ньютона-Лейбница. Для преобразования частногоиспользована формула конечных приращений Коши, причем некоторая точка, принадлежащая отрезку . Очевидно, чтопри. Поэтому, согласно доказанному (8.1.27),при.

Легко проверить, что

.

Отсюда и из доказанных утверждений следует, что

при . (8.1.28)

Подставив формулу (8.1.28) в формулу (8.1.26) получим

при . (8.1.29)

Таким образом, необобщенная формула трапеций имеет третий порядок точности при .

Оценка погрешности и определение порядка точности обобщенной формулы трапеций. Преобразуем разность между точным и приближенным значениями интеграла, вычисленным с помощью обобщенной формулы трапеций:

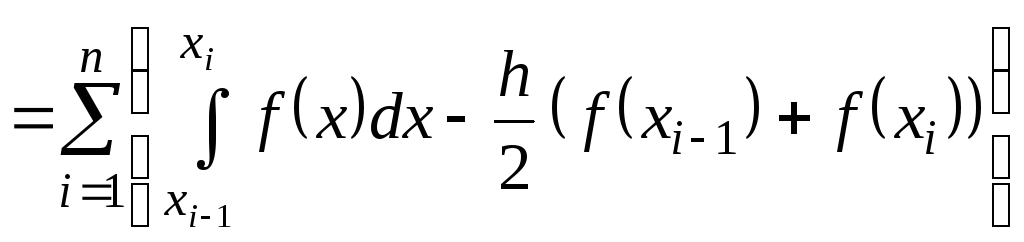. (8.1.30)

Отсюда, использовав формулу (8.1.20), получим оценку погрешности обобщенной формулы трапеций

. (8.1.31)

Здесь  мажорантные оценки модуля второй производной подынтегральной функции на отрезках разбиения , а мажорантная оценка модуля на всем отрезке(на отрезке . В процессе преобразований использовалось неравенство треугольника, что модуль суммы не превышает суммы модулей,для любого номераi, , а также, что.

С помощью формулы (8.1.29) разложим разность между точным и приближенным значениями интеграла, вычисленным с помощью обобщенной формулы трапеций, по степеням h:

при . (8.1.32)

В процессе преобразований использовалась теорема о среднем, согласно которой найдется точка на отрезкетакая, что будет наблюдается равенство. Для применения теоремы необходимо, чтобыбыла непрерывна на отрезке. Кроме того, использовалось асимптотическое равенствопри. Это равенство справедливо при условии. Докажите его самостоятельно.

Таким образом, обобщенная формула трапеций имеет второй порядок точности при .