Обобщенные формулы прямоугольников, трапеций, Симпсона

Полученные квадратурные формулы не содержат параметров, за счет изменения которых можно было бы регулировать погрешность получаемых приближенных значений интеграла. Поэтому с их помощью невозможно получить приближенное значение интеграла с заданной точностью. Но из этих квадратурных формул можно получить необходимые нам квадратурные формулы с регулируемой точностью, которые называются обобщенными. Принцип получения обобщенной квадратурной формулы из необобщенной формулы прост.

Рассмотрим его на конкретных примерах.

Отрезок разобьем наn равных отрезков точками , где

, . (8.1.12)

Здесь h – расстояние между соседними точками разбиения, называемое шагом. Тогда, в силу аддитивности определенного интеграла, искомый интеграл можно представить в виде

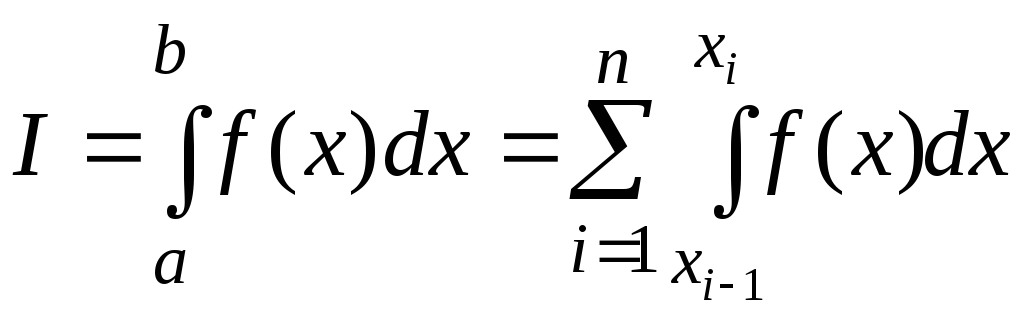. (8.1.13)

Заменим точные значения интегралов, стоящих в сумме (8.1.13), на приближенные, получаемые по формуле левых прямоугольников:

. (8.1.14)

Полученная квадратурная формула (8.1.14) называется обобщенной формулой левых прямоугольников.

Заменим точные значения интегралов, стоящих в сумме (8.1.13), на приближенные, получаемые по формуле правых прямоугольников:

. (8.1.15)

Полученная квадратурная формула (8.1.15) называется обобщенной формулой правых прямоугольников.

Заменим точные значения интегралов, стоящих в сумме (8.1.13), на приближенные значения, получаемые по формуле средних прямоугольников:

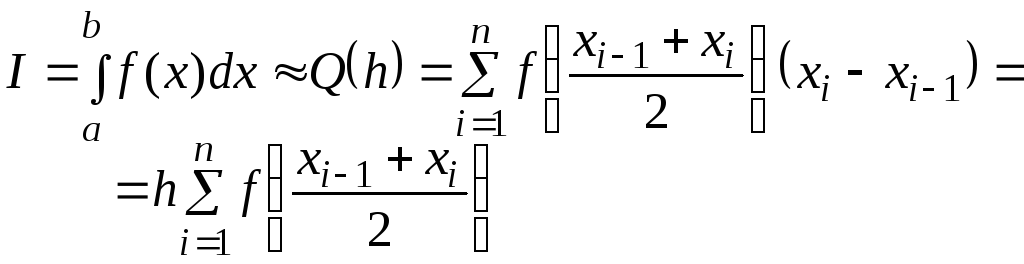(8.1.16)

Полученная квадратурная формула (8.1.16) называется обобщенной формулой средних прямоугольников.

Заменим точные значения интегралов, стоящих в сумме (8.1.13), на приближенные значения, получаемые по формуле трапеций:

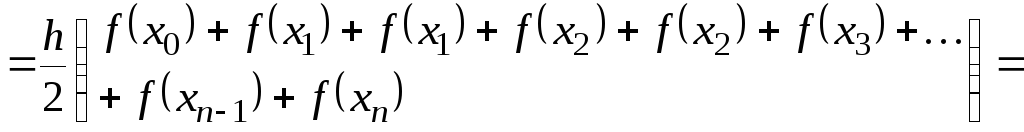
. (8.1.17)

Полученная квадратурная формула (8.1.17) называется обобщенной формулой трапеций.

Для получения обобщенной формулы Симпсона отрезок разбивается наравных отрезков точками, где

, . (8.1.18)

Здесь h – расстояние между соседними точками разбиения, называемое шагом. Тогда, в силу аддитивности определенного интеграла, искомый интеграл можно представить в виде

. (8.1.19)

Заменим точные значения интегралов, стоящих в сумме (8.1.19), на приближенные значения, получаемые по формуле Симпсона:

. (8.1.20)

Полученная квадратурная формула (8.1.20) называется обобщенной формулой Симпсона.

Геометрический смысл обобщенных квадратурных формул левых, правых и средних прямоугольников, а также обобщенных формул трапеций и Симпсона отражен на рисунках 8.6 – 8.10. Он является прямым следствием геометрического смысла необобщенных квадратурных формул. Приближенные значения интеграла , получаемые с помощью обобщенных квадратурных формул, численно равны площадям соответствующих закрашенных фигур. Функции, графики которых ограничивают закрашенные фигуры сверху, представляют собой интерполяционные функции – результаты кусочно-многочленной интерполяции. В случае формулы трапеций это функция, вычисляемая по формуле (4.4.8) и являющаяся результатом кусочно-линейной интерполяции. А в случае формулы Симпсона график ограничивающей функции составлен из кусков парабол, состыкованных в узлах с четными номерами.

Формула левых прямоугольников. Формула правых прямоугольников.

Рис. 8.6 Рис. 8.7

Формула средних прямоугольников Формула трапеций

Рис. 8.8 Рис. 8.9

Обобщенные квадратурные формулы имеют два параметра: n (m) и h, жестко связанных друг с другом формулами (8.1.11), (8.1.17). Рассматривая рисунки 8.6 – 8.10, можно предположить, что при или(при) площади закрашенных фигур стремятся к площади криволинейной трапеции, ограниченной сверху графиком подынтегральной функции, слева и справа- вертикальными прямыми и, а снизу – осьюOx. Таким образом, можно предположить, что при. Если это действительно так, то каждую из обобщенных квадратурных формул можно применить для вычисления приближенного значения интеграла с любой точностью. Для того чтобы в этом убедиться и реально применить обобщенные квадратурные формулы для вычислений интегралов, необходимо оценить погрешности получаемых приближенных значений интеграла и найти порядки точности квадратурных формул.

Рис. 8.10