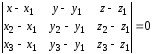3. Плоскость в пространстве

Любое уравнение первой степени в трехмерном пространстве определяет какую-либо плоскость.

Разным способам задания плоскости соответствуют различные виды уравнений (табл. 3.)

Таблица 3

№ п/п	Вид уравнения	Смысл входящих в уравнение коэффициентов	Примечание
1	Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору А(х-х0)+В(у-у0)+С(z-z0)=0	(x0,y0,z0) – координаты заданной точки; АВС – координаты заданного вектора	Вектор N(А,В,С) называется нормальным вектором плоскости
2	Общее уравнение плоскости Ах+Ву+Сz+D=0	D=-Ax0-By0-Cz0, АВС – нормальный вектор плоскости;	Это уравнение получается из уравнения (1) эле-ментарными
№ п/п	Вид уравнения	Смысл входящих в уравнение коэффициентов	Примечание
		х0,y0,z0 – координаты данной точки	преобразованиями
3	Уравнение плоскости, проходящей через три заданные точки	М1(х1,y1,z1), М2(х2,y2,z2), М3(х3,y3,z3) – три точки, заданные своими координатами	Точки М1, М2, М3 не должны лежать на одной прямой
4	Уравнение плоскости в отрезках на осях	а,b,c – отрезки, отсекаемые плоскостью от осей координат	аbc≠0

Пусть даны две плоскости ₁ и ₂:

₁: А₁х +В₁у+С₁z+D₁=0,

₂: А₂х +В₂у+С₂z+D₂=0.

Угол между двумя плоскостями определяется как.

Условие перпендикулярности двух плоскостей:

=0, то есть =0.

Условие параллельности двух плоскостей:

или.

Расстояние от точки до плоскости:

,

где Ах+Ву+Сz+D=0 – заданная плоскость; М(x₀,y₀,z₀) – данная точка.

Примеры решения типовых задач

1. Написать уравнение плоскости, проходящей через точку М(-1;1,3) перпендикулярно вектору .

Решение:

Найдем координаты вектора : О(0;0;0); М(-1;1;3)

{-1;1;3}.

Уравнение плоскости имеет вид:

A(x-x₀)+B(y-y₀)+C(z-z₀)=0

А=-1, В=1, С=3 – координаты вектора нормали.

X₀=-1, y₀=1, z₀=3.

-1(х+1)+1(у-1)+3(z-3)=0

-х-1+у-1+3z-9=0

-х+у+3z-11=0.

Ответ: -х+у+3z-11=0.

2.Написать уравнение плоскости, проходящей через точки М₁(1;-1;3), М₂(2;-1;0), М₃(4;2;-1).

Решение:

Уравнение плоскости, проходящей через три точки имеет вид:

,

,

9(х-1)-5(у+1)+3(z-3)=0

9х-9-5у-5+3z-9=0

9х-5у+3z-23=0.

Ответ: 9х-5у+3z-23=0.

3. Написать уравнение плоскости, проходящей через точку М₀(-2;7;3) параллельно плоскости х-4у+5z+1=0 (рис.10).

{1;-4;5}

М₀(-2;7;3)

Рис. 10

Решение:

Нормальный вектор для плоскости х-4у+5z+1=0 {1;-4;5} является нормальным для искомой плоскости. Так как плоскость проходит через точку М₀(-2;7;3), то уравнение плоскости имеет вид:

A(x-x₀)+B(y-y₀)+C(z-z₀)=0;

1(х+2)-4(у-7)+5(z-3)=0;

х+2-4у+28+5z-15=0;

х-4у+5z+15=0.

Ответ: х-4у+5z+15=0.

4. Найти расстояние от точки М₀(1;-1;3) до плоскости 13х+2у- -5z+1=0.

; х₀=1; у₀=-1; z₀=3.

А=13; В=2; С=-5, D=1.

.

Ответ: d=.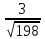

5. Найти угол между плоскостями х+у-1=0 и 2х-у+3z-1=0.

Решение:

Угол между плоскостями определяем как угол между нормалями к этим плоскостям. Из общих уравнений плоскостей определяем координаты нормалей {1;1;0},{2;-1;3}.

.

.

Ответ:.