2.2. Кривые второго порядка на плоскости

Уравнение вида Ах²+2Вху+Су²+2Dх+2Еу+F=0 называется общим уравнением кривой второго порядка. Коэффициенты уравнения – действительные числа, причем хотя бы одно из чисел А,В,С отлично от нуля. Такое уравнение определяет на плоскости окружность, эллипс, гиперболу или параболу.

В табл. 2 приведены уравнения кривых второго порядка и определен смысл входящих в них коэффициентов.

Таблица 2

№ п/п	Определение кривой	Вид уравнения	Примечание
1	Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная (рис.4)	- каноническое уравнение эллипса	2а – большая ось; 2b – малая ось 2с–межфокус-ное расстояние с2=а2-b2; - эксцентриси-тет, 0<<1. Т. А1,А2,В1,В2 – вершины эллипса
2	Гипербола – множество точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная (рис.5)	- каноническое уравнение гиперболы	2а–действи-тельная ось; 2b–мнимая ось; 2с –меж-фокусное расстояние с2=а2+b2; - эксцентри-ситет, >1. Точки А1,А2 – вершины гиперболы. Прямые - асимптоты
3.	Парабола - множество точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директриссой.	у2=2px – каноническое уравнение параболы, симметричной относительно оси ОХ x2=2pу – каноническое уравнение параболы, симметричной относительно оси ОY (рис.6б)	F - фокус, ди-ректриса. Точка (0;0) – вершина параболы (рис.6а) F - фокус, ди-ректриса. Точка (0;0) – вершина параболы (рис.6б)

1. Найти координаты фокусов и эксцентриситет эллипса 36х²+100у²=3600.

Решение:

Приведем уравнение эллипса к каноническому виду:

36х²+100у²=3600, поделим обе части уравнения на 3600:

, a²=100, b²=36.

F_л(-с,0) – левый фокус;

F_п(с,0) – правый фокус;

С=.

F_л(-8,0); F_п(8,0).

Эксцентриситет: .

Ответ: F_л(-8,0); F_п(8,0); =0,8.

2.Написать уравнение прямой, проходящей через левую вершину эллипса 16х²+25у²=400 и точку М₀(1;-3) (рис.7).

Решение:

у

4

М

5

-5

х

М₀

-4

Рис. 7

Приведем уравнение 16х²+25у²=400 к каноническому виду.

, a²=25, b²=16.

Левая вершина эллипса (-а,0)(-5,0). Обозначим М(-5,0). Составим уравнение прямой, проходящей через точки М₀ и М:

.

Ответ: .

3. Написать уравнение прямой, проходящей через правый фокус гиперболы 9х²-16у²=144 и параллельно прямой 3х-2у+6=0 (рис.8).

Решение:

у

3

F_П

-4

5

х

-3

Рис.8

Приведем уравнение 9х²-16у²=144 к каноническому виду ,a²=16, b²=9.

Правый фокус гиперболы F_п(с,0);

С=.

Итак, F_п(5,0).

1-й способ.

Условие параллельности двух прямых: k₁=k₂.

Пусть уравнение искомой прямой имеет вид y=k₂x+b₂;

3х-2у+6=0;

2у=3х+6;

у=(3/2)х+3;

k₁=3/2k₂=3/2.

Значит, y=(3/2)x+b₂ проходит через точку F_п(5,0), то 0=(3/2)5+b₂b₂=-15/2. Итак, 3x-2у-15=0.

2-й способ.

Искомая прямая проходит через точку F_л(5,0) параллельно прямой 3х-2у+6=0. Из общего уравнения заданной прямой определяем вектор нормали , который будет являться нормалью и для параллельной ей искомой прямой. Пользуемся уравнениемА(х-х₀)+В(у-у₀)=0, 3(х-5)-2(у-0)=0, 3х-2у-15=0.

Ответ: 3х-2у-15=0.

4. Написать уравнение прямой l, проходящей через нижнюю вершину эллипса 4х²+20у²=80, перпендикулярно прямой 2х-у+1=0 (рис.9).

y

2

l

х

М

-2

Рис. 9

Решение:

Приведем уравнение к каноническому виду 4х²+20у²=80,

, a²=20, b²=4.

Нижняя вершина имеет вид: М(0;-b)=М(0;-2).

1-й способ.

Условие перпендикулярности двух прямых: k₁k₃=-1.

2х-у+1=0

у=2х+1k₁=2.

Пусть уравнение прямой имеет вид: y=k₂x+b₂;

k₂=-1: k₁k₂=-1/2,

Так как прямаяпроходит через точку М(0;-2), то.

Итак, х+2у+4=0.

2-й способ.

По условию задачи требуется написать уравнение прямой l, проходящей через точку М(0;-2) перпендикулярно прямой 2х-у+1=0. Из общего уравнения прямой определяем координаты вектора нормали . Несложно представить (рис.9), что если искомая прямаяl перпендикулярна заданной, то вектор параллелен искомой прямой, т.е. является ее направляющим вектором. Используя уравнение прямой, проходящей через точку М₀(х₀,у₀) параллельно вектору 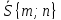, получим:

. У нас ;;

-х=2у+4, х+2у+4=0.

Ответ: х+2у+4=0.

5. Написать уравнение прямой, проходящей через правый фокус эллипса под углом 45˚ к оси Ох.

Решение:

a²=16, b²=25.

Правый фокус эллипса имеет вид F_п(с,0);

С=.

Итак, F_п(3,0).

Так как прямая проходит под углом 45˚ к оси Ох, то k=tgα=tg45˚=1.

Пусть уравнение искомой прямой имеет вид: y=kx+b;

k=1y=x+b.

Так как прямая проходит через точку F_п(3,0), то 0=3+bb=-3.

Значит, y=x-3.

Ответ: y=x-3.