1. Найти кратчайший путь из вершины в вершинув заданном графе.
Решение. Используем алгоритм задачи о нахождении кратчайшего пути из А в В в смысле наименьшего количества ребер.
Вершине А припишем индекс 0.
2. Всем вершинам, смежным с вершиной А, припишем индекс 1.
3. Всем вершинам, смежным с вершинами индекса 1 и не имеющим индекса, припишем индекс 2.
4. Всем вершинам, смежным с вершинами индекса 2 и не имеющим индекса, припишем индекс 3. В нашем случае, в этот момент вершина В также получит индекс 3.
Процесс останавливаем (несмотря на то, что остались непомеченные вершины).
Таким образом, мы нашли длину кратчайшего пути.
Построим сам путь.
5. Вершина В имеет индекс 3. Среди смежных с ней вершин есть вершина индекса, на единицу меньшего, чем 3, то есть, индекса 2. Перейдём из В к этой вершине ( в нашем случае такая вершина одна).
6. Среди вершин, смежных с найденной вершиной индекса 2 есть вершина индекса, на единицу меньшего, то есть, индекса 1 (такая вершина также в нашем случае единственна). Перейдём к ней.
7. Вершина индекса 1 смежна с вершиной А. Переходя от неё к А, заканчиваем построение кратчайшего пути в заданном невзвешенном графе.
V. Расчётно-графическая работа. Задание 1.
9. «Эйлерова цепь (цикл). Формула Эйлера. Плоские и планарные графы»
Необходимые определения и формулировки теорем.
1. Что такое эйлерова цепь?
2. Что такое эйлеров цикл?
3. У каких графов существует эйлерова цепь?
4. У каких графов существует эйлеров цикл?
5. В чем состоит формула Эйлера?
6. Для каких объектов верна формула Эйлера?
7. Как выглядят непланарные графы № 1, № 2, типов 1, 2?
8. В чем состоит теорема Куратовского-Понтрягина?
Задачи для усвоения материала.
ЗАДАЧА ЭЙЛЕРА
1. Обладают ли эйлеровой цепью (или эйлеровым циклом) следующие графы:
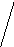
а)
б) в)
г)
д)
е)
ж)
ФОРМУЛА ЭЙЛЕРА
|
Для любого плоского или планарного связного графа (к которым, заметим, относятся все многогранники в пространстве) верна формула В + Г– Р = 2, где В – число вершин, Г – число граней, Р – число ребер графа. |
2. Считая данные графы планарными, выяснить, сколько граней получится после преобразования их в плоские («распутывания»):
|
|
|
3*. а) Пусть k – число граней правильного многогранника, сходящихся в одной вершине. Доказать геометрически, что всегда 3 £ k £ 5.
б) Правильный многогранник называется октаэдром (от греческого "окта" – восемь, "эдр" – грань). Выяснить форму его граней.
в) То же для додекаэдра (додека – двенадцать) и икосаэдра (икоса - двадцать).
г) Выявить все возможные правильные многогранники.
НЕПЛОСКИЕ ГРАФЫ
4. Являются ли данные графы плоскими (планарными)?
г)
д)
е)
ж)
з)
10. «Раскраски графа».
Необходимые определения и формулировки теорем.
В чем состоит задача о раскраске вершин графа?
Каков алгоритм решения задачи о раскраске графа?
В чем состоит задача о раскраске ребер графа?
Что Вы знаете о хроматическом индексе?
Задачи для усвоения материала.
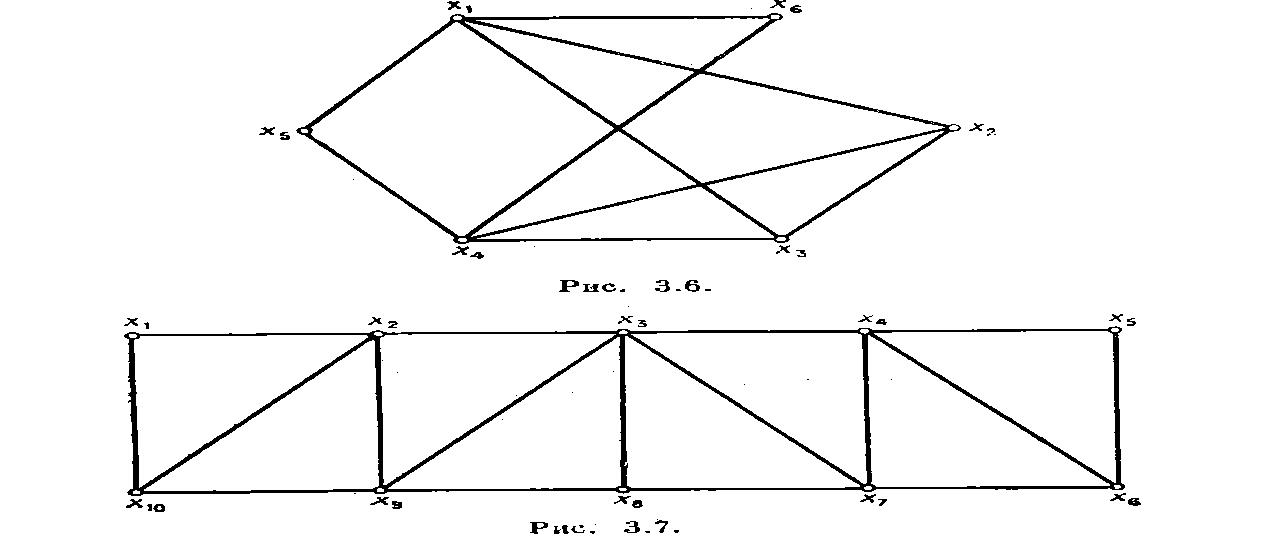
1. Для каждого из предложенных графов найдите правильные раскраски рёбер и вершин.
Здесь, к сожалению, придется рисунки переделать вручную: номера их какие-то странные, на некоторых рисунках уже построены правильные раскраски.
]
