
- •Часть I. Теория множеств
- •Предисловие
- •Тема 1 Основы теории множеств и комбинаторики.
- •1 «Операции над множествами»
- •2. «Отображения множеств».
- •IV. Решение некоторых типовых заданий.
- •2. Задано отображение f: rr,
- •3. «Декартово произведение множеств».
- •II. Задачи для усвоения материала.
- •IV. Решение некоторых типовых заданий.
- •5. «Мощность множеств»
- •IV. Решение некоторых типовых заданий.
- •1*. Используя методы теории множеств, решить задачу:
- •6. «Отношения на множестве»
- •I. Необходимые определения и формулировки теорем.
- •II. Задачи для усвоения материала.
- •III. Самостоятельная работа 6.
- •IV. Решение некоторых типовых заданий.
- •1. Выяснить, какими свойствами обладает отношение на множествеA, если .
- •2. На множестве людей рассмотрим отношение "быть одинакового роста". Является ли оно отношением эквивалентности? Если да, то что служит классом эквивалентности?
- •7. Итоговое повторение темы 1. Контрольная работа № 1.
- •Основная литература
- •Дополнительная литература
2. Задано отображение f: rr,
Определить, является ли отображение
 инъективным.
инъективным.Определить, является ли отображение
 сюръективным.
сюръективным.Определить, является ли отображение
 биективным.
биективным.Найти образ отрезка
 .
.Найти прообраз отрезка

Решение.
Для определения инъективности исследуем функцию
 на
монотонность. Вычислим производную
функции
на
монотонность. Вычислим производную
функции
 :
:
 .Производная
.Производная
 определена и непрерывна при
определена и непрерывна при
 и обращается в нуль при
и обращается в нуль при .
При
.
При и при
и при производная
производная
 положительна,
а, следовательно,
функция
положительна,
а, следовательно,
функция
 возрастает.
При
возрастает.
При
 производная
производная
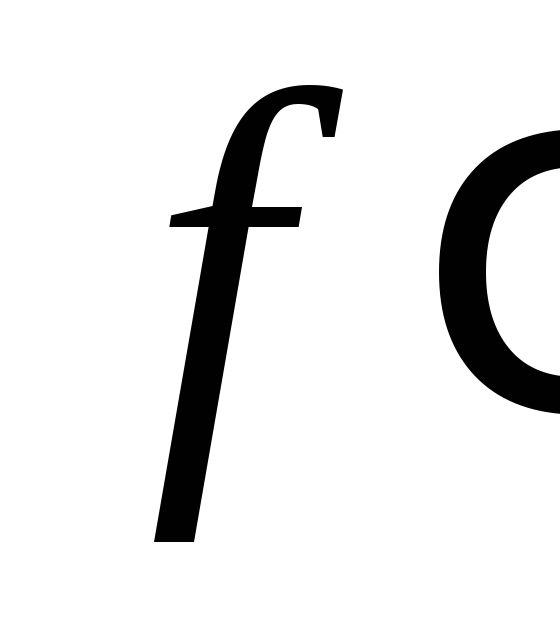 отрицательна,
а, следовательно,
функция
отрицательна,
а, следовательно,
функция
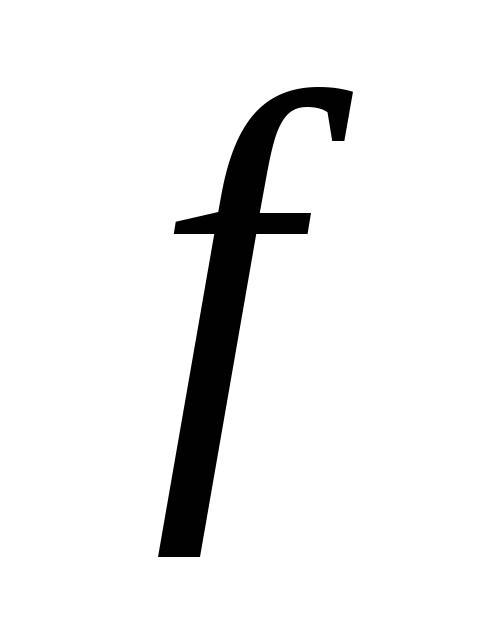 убывает.
График функции
убывает.
График функции
 меняет направление с возрастания на
убывание и обратно (можно даже построить
его эскиз), следовательно, найдутся
два значения
меняет направление с возрастания на
убывание и обратно (можно даже построить
его эскиз), следовательно, найдутся
два значения
 и
и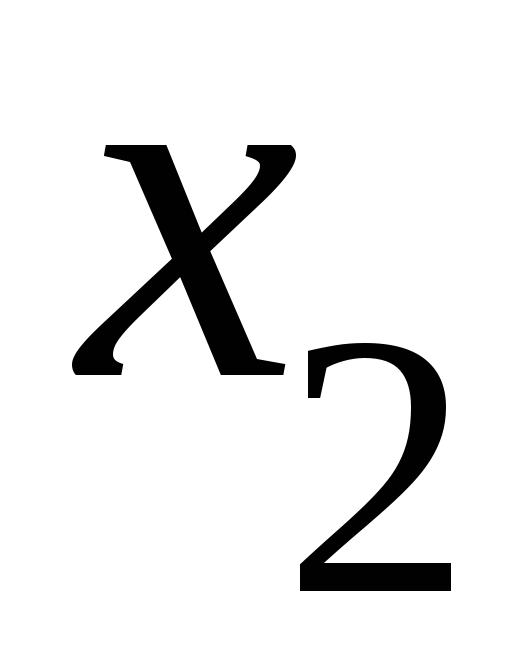 такие, что
такие, что ,
а
,
а (например,
(например,
 ).
).
Таким образом,
отображение
![]() неинъективно.
неинъективно.
График функции y=f(x) принимает все значения от – до +, поэтому можно утверждать что для любого y=
 найдётся соответствующее значение
найдётся соответствующее значение .
Таким образом, отображение
.
Таким образом, отображение
 сюръективно.
сюръективно.Так как отображение
 неинъективно, то оно не является
биективным.
неинъективно, то оно не является
биективным.На отрезке
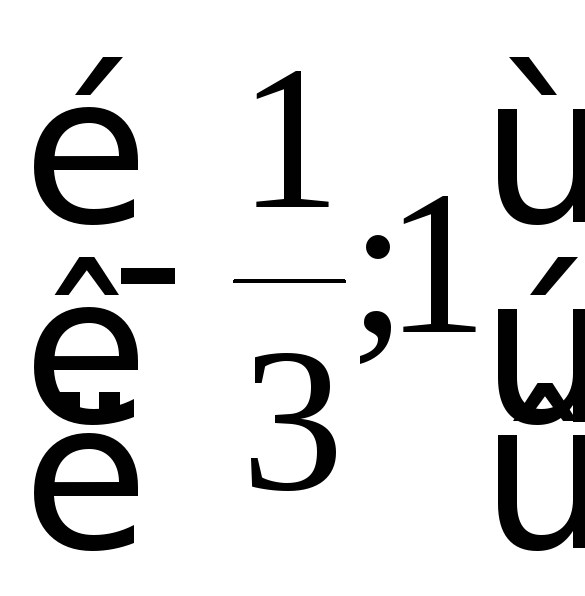 только одна точка экстремума графика
функции
только одна точка экстремума графика
функции
 .
Это точка минимума. Поэтому в этой
точке отображение примет наименьшее
значение. Для нахождения наибольшего
значения подставим значения концов
отрезка в формулу f(x):
.
Это точка минимума. Поэтому в этой
точке отображение примет наименьшее
значение. Для нахождения наибольшего
значения подставим значения концов
отрезка в формулу f(x):
 ;
;
 ;
;
![]() .
.
Образы элементов
отрезка
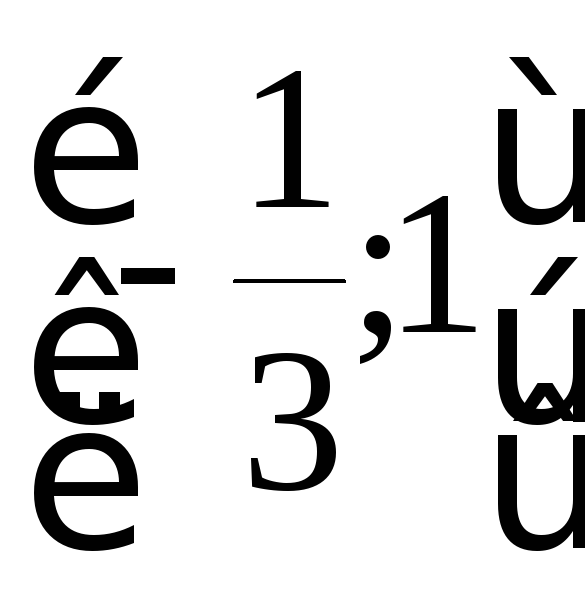 расположатся между наименьшим и
наибольшим значениями, поэтому образом
отрезка
расположатся между наименьшим и
наибольшим значениями, поэтому образом
отрезка является отрезок
является отрезок (то есть
(то есть ).
).
Для нахождения прообраза отрезка
 воспользуемся результатами, полученными
в предыдущих пунктах.
воспользуемся результатами, полученными
в предыдущих пунктах. ,
если
,
если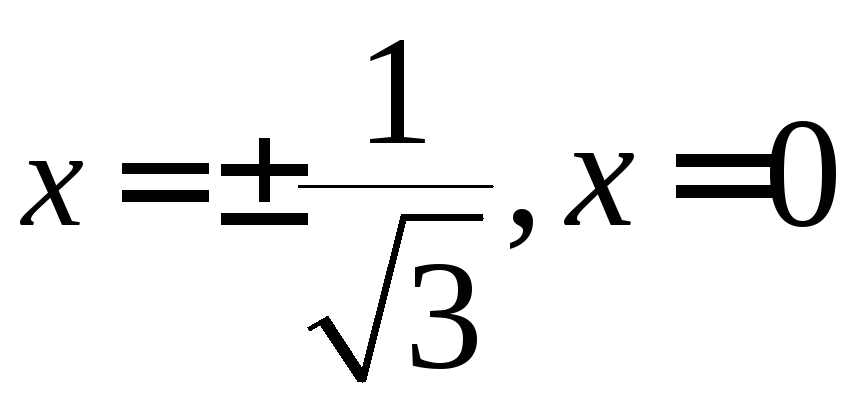 ,
причём функция принимает неотрицательные
значения при
,
причём функция принимает неотрицательные
значения при
 и при
и при .
Значение 2 функция принимает при
.
Значение 2 функция принимает при ,
причём на отрезке
,
причём на отрезке отображение инъективно. Итак, прообразом
отрезка
отображение инъективно. Итак, прообразом
отрезка
 является множество чисел
является множество чисел
 то есть
то есть .
.
Примечание.
Данную задачу проще решить, построив график отображения y=f(x).
3. «Декартово произведение множеств».
I. Необходимые определения и формулировки теорем.
Что такое «декартово произведение множеств А и В»?
II. Задачи для усвоения материала.
Заданы множества А и В. Составить декартовы произведения
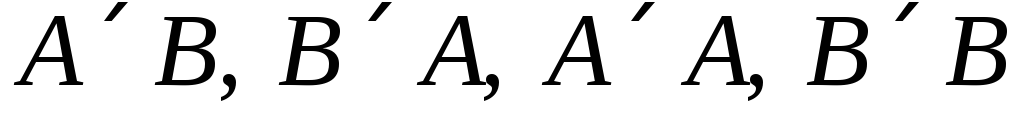 :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Доказать равенства:
а)
![]() ;
;
б)
![]() .
.
3. Изобразить на координатной плоскости множество
![]() .
Декартовым произведением каких двух
множеств из R
оно является?
.
Декартовым произведением каких двух
множеств из R
оно является?
III. Самостоятельная работа 3.
Вариант 0
1 Составить
декартово произведение множеств
![]() ,
если
,
если
![]() .
.
2 Изобразить на координатной плоскости множество
![]() .
Декартовым произведением каких двух
множеств из R
оно является?
.
Декартовым произведением каких двух
множеств из R
оно является?
Решение некоторых типовых заданий.
Составить декартово произведение множеств
 ,
,
если
![]() .
.
Решение.
Согласно определению декартового произведения множеств, получаем:
 .
.
4. «Основы комбинаторики»
Необходимые определения и формулировки теорем.
Что изучает комбинаторика?
Сформулируйте правило произведения.
Что такое перестановки?
Что Вы знаете о числе перестановок элементов без повторений?
Что Вы знаете о числе перестановок с повторениями?
Что такое сочетания?
Что Вы знаете о числе сочетаний?
Что такое размещения?
Что Вы знаете о числе размещений?
