
П.Г.Фрик - Турбулентность модели и подходы, часть 2
.pdfМ инистерство общ его и профессионального образования Российской Ф едерации
П ермский государственный технический университет
Кафедра математического моделирования систем и процессов
Ï .Ã.Ô ðèê
ТУРБУЛЕН ТН О СТЬ: М ОДЕЛИ И П ОДХОДЫ
Курс лекций
Часть II
Рекомендовано учебно-методическим советом по направлению «Электроника и прикладная математика» в качестве учебного пособия для студентов специальности «П рикладная математика»
Ï åðìü 1999
2
ÓÄÊ 532.517.4 Ô 88
Турбулентность: модели и подходы. Курс лекций. / П .Г.Ф рик; П ерм. гос. техн. ун-т. Часть II. П ермь, 1999. 136 с.
Вторая частькурса лекций вклю чаетвсебя введение и четыре из семи разделов курса «Турбулентность: модели и подходы»(три первых раздела: «Основы», «Хаос в динамических системах»и «П олуэмпирическиемодели» вош ли в первую часть курса). В четвертом разделе излагаются модели однородной и изотропной турбулентности, начиная стеории Колмогорова и кончая современными моделями перемежаемости в развитой турбулентности. П ятый раздел посвящ ен некоторым специальным турбулентным потокам. Рассмотрены особенности поведения двумерной турбулентности и турбулентности, вызванной силами Архимеда. В ш естом разделе излагаю т- сямодели, основанные на применении специальных функциональных базисов, названных иерархическими, и дается краткое изложение вейвлетанализа, с примерами его применения к гидродинамическим системам. П о- следний, седьмой раздел посвящ ен каскадным моделям турбулентности - простейш им моделям развитой турбулентности, доказавш им свою эффективность в моделировании свойств турбулентности в инерционных интервалах при очень высоких числах Рейнольдса.
Для студентов и аспирантов физико-математических специальностей. И л.89. Библиогр.: 35 назв.
Рецензенты: |
кафедра общ ей физики П ермского |
|
государственного технического университета, |
|
д-р физ.-мат.наук, профессор Д.В.Любимов |
ISBN 5-88151-193-Õ |
|
|
© |
П ермский государственный |
|
1. |
технический |
университет, |
1999 |
|
|
3
ВВЕДЕН И Е |
4 |
|
1. |
ÎÑÍ Î ÂÛ |
5 |
2. |
ХАОС В ДИ Н А М И Ч ЕСКИ Х СИСТЕМ АХ |
5 |
3. ПОЛУЭМ П И РИ Ч ЕСК И Е М ОДЕЛИ |
5 |
|
4. |
ОДН О РОДНАЯ ТУРБУЛЕН ТН О СТЬ |
6 |
|
4.1. ÎД Н ОРОДНАЯ И ИЗОТРОПНАЯ ТУРБУЛЕНТНОСТЬ |
6 |
|
4.2. ÁАЛАНС ЭНЕРГИ И П О М АСШ ТАБАМ . ÊАСКАД |
9 |
|
4.3. ÒЕОРИЯ ÊОЛМ ОГОРОВА 1941 ÃÎÄÀ (Ê41) |
13 |
|
4.4. ËОГН О РМ АЛЬНАЯ М ОДЕЛЬ (Ê62) |
22 |
|
4.5. Ô РАКТАЛЫ И ТУРБУЛЕНТНОСТЬ |
27 |
|
4.6. ËОГПУАССОНОВСКИЕ М ОДЕЛИ |
35 |
5. |
ДВУМ ЕРНАЯ ТУРБУЛЕН ТН О СТЬ |
45 |
|
5.1. ÇАКОН Ы СОХРА Н ЕН И Я И И Н ЕРЦ И О Н Н Ы Е И Н ТЕРВАЛЫ |
46 |
|
5.2. ËАБОРАТОРН Ы Е ЭКСПЕРИ М ЕНТЫ |
51 |
|
5.3. ×ИСЛЕН Н Ы Е ИССЛЕДОВАНИЯ |
53 |
|
5.4. Ï ЕРЕМ ЕЖ АЕМ ОСТЬ В ДВУМ ЕРН О Й ТУРБУЛЕН ТНОСТИ |
59 |
|
5.5. ÊО Н ВЕКТИ ВНАЯ ТУРБУЛЕН ТНОСТЬ |
65 |
6. |
И ЕРАРХ И Ч ЕСК И Е М ОДЕЛИ ТУРБУЛЕН ТН О СТИ И ВЕЙ ВЛЕТЫ |
71 |
|
6.1. È ЕРАРХИЧЕСКИ Й БАЗИС ДЛЯ ТУРБУЛЕН ТН Ы Х ПОЛЕЙ |
71 |
|
6.2. È ЕРАРХИЧЕСКАЯ М ОДЕЛЬ ДВУМ ЕРН О Й ТУРБУЛЕНТНОСТИ |
80 |
|
6.3. ÂЕЙ ВЛЕТЫ |
87 |
|
6.4. Í ЕП РЕРЫ ВНОЕ ВЕЙВЛЕТ-П РЕОБРАЗОВАНИЕ |
90 |
|
6.5. ÄИСКРЕТН О Е ВЕЙВЛЕТ-П РЕОБРАЗОВАНИЕ |
95 |
|
6.6. ÂÅÉ ÂËÅÒ-АНАЛИЗ ВРЕМ ЕН Н Ы Х КОЛЕБА Н И Й ГИДРОДИНАМ ИЧЕСКИ Х СИСТЕМ |
102 |
7. |
КАСКАДН Ы Е М ОДЕЛИ ТУРБУЛЕН ТН О СТИ |
109 |
|
7.1. ÊАСКАДН Ы Е М ОДЕЛИ |
109 |
|
7.2. Ì ОДЕЛЬ Í ОВИКОВА - ÄЕСН Я Н СКОГО |
110 |
|
7.3. Ì ОДЕЛЬ GOY |
113 |
|
7.4. ÑКЕЙ Л И Н Г И П ЕРЕМ ЕЖ АЕМ ОСТЬ В КАСКАДН Ы Х М ОДЕЛЯХ РАЗВИТОЙ ТУРБУЛЕН ТН О СТИ |
119 |
|
7.5 Ì ОДЕЛЬ КОНВЕКТИ ВНОЙ ТУРБУЛЕН ТНОСТИ |
124 |
|
7.6. ÊАСКАДН Ы Е П РО Ц ЕССЫ В Ì ÃÄ-ТУРБУЛЕНТНОСТИ |
130 |
8. |
ЗАКЛЮ ЧЕН И Е |
136 |
4
ВВЕДЕН И Е
Н астоящ ий курс лекций ставит своей целью дать представления о разнообразных подходах и методах, применяемых в исследованиях развитой турбулентности.
Курс состоит из двух частей. П ервая часть вклю чала три главы: 1.Основы, 2.Хаос в динамических системах, 3.П олуэмпирические модели. П ервая глава содержала базовые сведения об уравнениях движения идеальной и реальной жидкости и краткий обзор методов и некоторых результатов исследования устойчивости гидродинамических систем. Во второй главе обсуждались методы и подходы теории динамических систем, позволивш ей значительно углубить понимание процессов перехода от детерминированного поведения к хаотическому. Третья глава кратко знакомила с подходом Рейнольдса к описанию средних полей в развитых турбулентных течениях и вытекаю щ ими из него полуэмпирическими моделями турбулентности.
Н ужно отметить, что в первую часть курса были включены в основном сведения, которыеможно найти в различных учебниках и монографиях. Н астоящ ая, вторая часть содержит результаты, которые, за редким исклю чением, не вош ли ещ е в книги и могут быть найдены только в оригинальных статьях. Эта часть, предлагаемая вниманию читателя, состоит из четырех глав (с четвертой по седьмую , так как для обеих частей принята сквозная нумерация).
Четвертая глава посвящ ена моделям однородной и изотропной турбулентности. Здесьсобраны модели мелкомасш табной турбулентности, на- чиная со знаменитой теории Колмогорова 1941 года. Описаны первые попытки учета перемежаемости (лог-нормальная модель, бета-модель). П оказано, что дало применение к теории турбулентности идеи фрактальности и как использование новых экспериментальных данных о структуре поля диссипации энергии и о поведении высш их статистических моментов привело к появлению новых моделей, основанных на лог-пуассоновской статистике турбулентных полей.
П ятый раздел посвящ ен некоторым специальным турбулентным потокам. Рассмотрены особенности поведения двумерной турбулентности, в которой наличие дополнительного закона сохранения приводит к качественно иному поведению мелкомасш табного течения. Н а примере турбулентности, вызванной силами плавучести (т.е. конвективной турбулентности), показано, как можетменяться динамика инерционного интервала под действием дополнительного силового поля.
5
В ш естом разделе излагаю тся модели, основанные на применении специальных функциональных базисов, воспроизводящ их структуру турбулентных потоков. Эти базисы получили название иерархических и по современной терминологии относятся к вейвлет-базисам. Вейвлет-анализ (возникш ий заметно позже первых иерархических моделей) превратилсяна сегодня в развитую область матфизики и его значение для исследования стохастических гидродинамических систем и турбулентности не исчерпывается применением вейвлет-базисов для численного моделирования тече- ний. Учитывая, что до настоящ его времени литература о вейвлетах на русском языке практически отсутствует, в этой же главе дается краткое изложение основ вейвлет-анализа, с примерами его применения к гидродинами- ческим системам.
П оследний, седьмой раздел посвящ ен каскадным моделям турбулентности - простейш им моделям развитой турбулентности, доказавш им свою эффективность в моделировании свойств турбулентности в инерционных интервалах при очень высоких числах Рейнольдса. Эти модели, являясьдинамическими системами относительно высокого порядка (несколько десятков уравнений), описываю т каскадные процессы в ш ироком интервале масш табов. Дано изложение методов построения моделей этого типа, приведены примеры построения моделей для различных турбулентных течений и рассмотрены некоторые результаты их применения.
Курс предназначен для студентов специальности "П рикладная математика", ориентирую щ ихся на работу в научно-исследовательских учреждениях и на кафедрах, в особенности тех, что связаны с реш ением задач механики жидкости и газа. В то же время, в курсе рассматриваю тся и общ ие подходы к моделированию сложных динамических систем, которые могут быть полезными специалистам, занимаю щ имся моделированием самых различных (и нетолько механических) систем и явлений.
1.ÎÑÍ Î ÂÛ
2.ХАОС В Д И Н А М И Ч ЕСКИХ СИСТЕМ АХ
3.ПОЛУЭМ П И РИ Ч ЕСК И Е М ОДЕЛИ
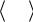
6
4. ОДН О РОДН А Я ТУРБУЛЕН ТН О СТЬ
4.1.Однородная и изотропная турбулентность
Íачиная изучение свойств мелкомасш табной турбулентности, сделаем несколько важных замечаний, частично повторяю щ их выводы, обсуждавш иеся в первой части курса. П реждевсего напомним, что мы ограничи- ваемся рассмотрением течений несжимаемой жидкости, описываемых уравнениями Н авьеСтокса, которыезапиш ем в виде
∂ v |
i |
+ v |
∂ |
v |
i |
= − ρ − 1∂ p + ν∂2 |
v |
i |
+ |
f |
, |
(4.1) |
|
t |
j |
j |
|
i |
jj |
|
|
i |
|
|
|||
∂k vk |
= 0 . |
|
|
|
|
|
|
|
|
|
(4.2) |
||
Здесь vi - компоненты скорости, |
f i - компоненты силы, ρ - плотность, |
||||||||||||
p - давление, ν - вязкость. П ри этом нужно незабывать, что сама возможность применения уравнений (4.1)-(4.2) к описанию турбулентных течений при огромныхзначениях числа Рейнольдсане является очевидной, так как при их выводе использовано предположение о том, что тензор вязких напряжений является линейной функцией только первых производных поля скорости (см. вводныезамечания к разделу 3).
Важно также подчеркнуть, что рассматривается развитая турбулентность, характеризуемая наполненными спектрами Ф урье(как временными, так и пространственными), что свидетельствует о сущ ествовании многомасш табной структуры поля скорости. И менно многомасш табность и является важнейш им признаком развитой турбулентности, приводя к возбуждению гигантского числа степеней свободы.
М ы уже говорили о том, что лю бой подход к описанию развитой турбулентности по сути представляет собой тот или иной способ ограниче- ния числа степеней свободы, приводящ ий к соответствую щ им моделям. В главе 3 был рассмотрен подход Рейнольдса, состоящ ий в представлении входящ их в (4.1)-(4.2) полей в виде сумм средних полей и пульсаций:
vi (r ,t) = U i (r , t) + ui (r ,t) , |
p(r ,t) = P(r , t) + |
|
p (r , t) , f (r , t) = F (r , t) + |
f (r , t) . (4.3) |
|||||||
П одход приводит к уравнениям длясредних величин |
|
||||||||||
∂U |
+ U |
j |
∂ U |
= − ρ− 1∂ P + ν∂2 U |
− ∂ |
j |
u u |
+ F , |
(4.4) |
||
t i |
|
j i |
|
i |
jj i |
|
j i |
i |
|
||
|
|
|
|
|
∂kU k |
= 0 , |
|
|
|
(4.5) |
|
7
вклю чаю щ им новый член - тензор напряжений Рейнольдса (угловые скобки по-прежнему обозначают осреднение по ансамблю реализаций). Различныеспособы замыкания уравнений (4.4)-(4.5) составляю т суть полуэмпирических моделей.
П одход Рейнольдса (и связанные с ним полуэмпирические модели) направлен на описание средних полей скорости, возникаю щ их в конкретных потоках. Каждая полуэмпирическая модель адаптируетсядля заданного (как правило, достаточно узкого) класса течений и включает ряд параметров, экспериментально определяемых именно для данного класса тече- ний и справедливых в определенном диапазонезначений числа Рейнольдса. Таким образом, делается попытка ограничиться описанием крупномас- ш табных полей, а влияние мелкомасш табных полей охарактеризовать с помощ ью небольш ого числа параметров.
Зададимся теперь вопросом о том, есть ли у турбулентности некие универсальные свойства, не зависящ ие от конкретных условий ее возбуждения? Очевидно, что рассчитывать на обнаружение таких универсальных свойств можно только вдали от границ и на масш табах, сущ ественно меньш их размеров области, занятых турбулентным течением. Таким образом, мы начинаем изучение мелкомасш табной турбулентности, в смысле, что основной интерес представляют для насмасш табы l << L ( L - внеш ний, или интегральный масш таб турбулентности). В то же время, говоря о развитой турбулентности, мы подразумеваем, что числа Рейнольдса столь велики, что остается ш ирокий диапазон возбужденных масш табов, удовлетворяю щ их этому условию . И начеговоря, λ << l << L , ãäå λ - микромасш таб турбулентности, характеризую щ ий масш табы пульсаций скорости, на которых становитсясущ ественной вязкая диссипация.
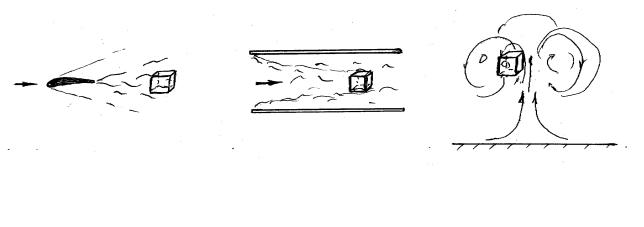
Н а рис.4.1 схематически показаны три различных турбулентных потока (турбулентный след, течение в трубе и конвективный факел) и области
Ðèñ.4.1
в них, изображенные в виде кубов, в которых можно надеяться на выявле-
8
ниетаких универсальных свойств. П ри наличии осредненного течения (поток в трубе) выделенный куб движетсясо средней скоростью этого потока.
Выделенные области не случайно имеют кубическую форму. Дело в том, что, желая избежать влияния границ, мы в то же время хотим рассматривать ограниченную область потока, причем свойства течения в этой области не должны зависеть от ее точного положения (другими словами, используетсягипотеза об однородности турбулентности на масш табах, много меньш их масш таба ее возбуждения L ). Н аиболее простой путь удовлетворения этих противоречивых требований состоит в рассмотрении кубиче- ской области с ребром D , на гранях которого выполняю тсяпериодические граничные условия. Это условие состоит в том, что для всякой функции и лю бых целых n, m, q
f (x + nD, y + mD, z + qD) = f (x, y, z) . |
(4.6) |
Такая постановка задачи очень удобна для прямых численных реш е- ний уравнений (4.1)-(4.2). И менно для куба с периодическими граничными условиями (для квадрата в случае двумерных течений) выполнены практи- чески все численные эксперименты по исследованию свойств однородной турбулентности. Заметим, что условие однородности немедленно приводит к тому, что уравнение (4.4) допускает только тривиальное реш ение
r
U (t, r ) = 0 . Кубическая геометрия и условие периодичности создаю т идеальныеусловия для применения спектральных (и спектрально-сеточных) мето-
дов, так как любая функция f (t, r ) |
можетбыть представлена в виде |
|
|||||||||||||
|
|
|
|
|
r |
) |
|
2πi |
( nx+ my+ qz ) |
) |
rr |
|
|||
|
|
|
|
f ( t,r ) = å |
f nmq ( t )e D |
|
= år fk ( t )eikr , |
(4.7) |
|||||||
|
|
|
|
|
|
n ,m ,q |
|
|
|
k |
|
|
|||
r |
2π |
r |
r |
r |
|
|
|
|
|
|
|
|
|
|
|
ãäå k = |
|
(nex |
+ me y |
+ qez ) |
есть волновой вектор, а коэффициенты Ф урье оп- |
||||||||||
D |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ределяютсяформулой |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
) |
1 |
|
D D D |
r |
rr r |
|
|
|
|||
|
|
|
|
fk ( t ) = |
|
|
òòò f ( t,r )e− ikr dr . |
|
|
(4.8) |
|||||
|
|
|
|
D3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
0 0 0 |
|
|
|
|
|
|
|
В свете поставленной задачи фурье-представление удобно тем, что каждая гармоника соответствует движению определенного пространственного масш таба. Для того, чтобы получить энергию всех движений заданного масш таба l = 2π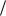 k , нужно просуммировать всегармоники, волновыевекторы которых равны по модулю
k , нужно просуммировать всегармоники, волновыевекторы которых равны по модулю
r |
|2 . |
(4.9) |
E( k ) = år | vk |
|k|=k

9
4.2. Баланс энергии по масш табам. Каскад
Для получения уравнения, описываю щ его баланс энергии в одном отдельно взятом масш табе, нужно записать уравнения Н авьеСтокса (4.1)- (4.2) в пространстве Ф урье. П ри этом можно воспользоваться рядами Ф у- рье вида (4.7), имея в виду кубическую геометрию с периодическими условиями, либо интегралами Ф урье, опираясьна рассмотрение турбулентного течения в ограниченной части бесконечного пространства. Чтобы не создать впечатление, что получаю щ иеся уравнения связаны с искусственно выбранной формой области, воспользуемся в данном параграфе интегралами Ф урье(вывод уравнений для рядов оставим для домаш них упражнений).
И так, пусть течение занимает ограниченную область, затухая на бесконечности, и все входящ ие в уравнения Н авье - Стокса величины допускаю т представление в виде
r |
1 |
∞ ) r |
|
rr r |
|
f ( r ,t ) = |
|
òf ( k ,t )eikr dk , |
(4.10) |
||
8π 3 |
|||||
ãäå |
|
− ∞ |
|
|
|
r |
∞ |
r |
rr r |
|
|
) |
|
||||
f ( k ,t ) = òf ( r ,t )e− ikr dr , |
(4.11) |
||||
|
|
− ∞ |
|
|
|
r = (x, y, z) - радиус-вектор, k = (k x , k y , k z ) - волновой вектор.
Всевеличины в уравнении (4.1) выразим черезфурье-образы (4.10)
∞ ) r rr r
r ¢ ik ′r ¢
¶t òv( k ,t )e dk +
− ∞
1
8π 3
∞ ) |
r |
r r |
r r ∞ |
) |
r |
r r |
r |
|
|
r |
′ |
ik ′r |
′ |
r |
′ |
ik ′r |
dk |
′ |
= |
òv( k ,t )e |
|
dk Ñ òv( k ,t )e |
|
|
|||||
− ∞ |
|
|
− ∞ |
|
|
|
|
|
|
r ∞ |
) |
r |
rr r |
∞ ) r |
rr r |
∞ ) r |
rr r |
|
|
|
r |
|
òf ( k ¢,t )eik ′r dk ¢ |
||
= - ρ − 1Ñ òp( k ¢,t )eik ′r dk ¢+ ν |
òv( k ¢,t )eik ′r dk ¢+ |
||||||
− ∞ |
|
|
|
− ∞ |
|
− ∞ |
|
и воспользуемсятеоремой о дифференцировании (см. параграф 2.4.2 части 1)
|
∞ ) r rr r |
|
i |
|
∞ ∞ |
r |
r r |
|
) r |
|
r r r r r |
||||||||
|
|
r |
|
|
ik ′r |
|
|
|
|
|
|
r |
|
i( k ′+ k ′)r |
|
|
|||
|
|
|
|
|
|
|
|
|
|
? |
|
|
|
|
|
|
|||
∂t |
|
v( k ′)e |
|
dk ′+ |
|
|
[ v( k ′)k ′]v( k ′)e |
|
dk ′dk ′= |
||||||||||
|
8π |
|
|
||||||||||||||||
|
ò |
|
|
|
|
|
3 ò ò |
|
|
|
|
|
|
|
|
|
|||
− ∞ |
|
|
|
|
|
|
|
− ∞ − ∞ |
|
|
|
|
|
|
|
|
|
||
|
|
i |
∞ r |
) |
r |
rr |
r |
|
∞ |
|
) r |
rr r |
∞ ) r |
rr r |
|||||
|
|
|
|
|
ik ′r |
|
|
|
2 r |
|
ik ′r |
|
|
|
ik ′r |
|
|||
= − |
|
|
′ |
|
′ |
|
|
′ |
′ |
|
′ |
|
′ |
|
′ |
|
′ |
||
|
ρ |
|
|
|
|
|
|
|
|||||||||||
|
òk p( k )e dk |
− ν òk |
|
v( k )e dk + |
òf ( k )e dk . |
||||||||||||||
|
|
|
− ∞ |
|
|
|
|
|
|
− ∞ |
|
|
|
|
|
− ∞ |
|
|
|
10
Для упрощ ения записи во всех функциях здесьи далееопускается ар-
rr
гумент t . Уравнение умножается на e− ikr и интегрируется по dr . Учитывая, что
∞ |
|
r r |
r |
|
r |
r |
r |
|
|
2π òe |
i( k′− k )r |
|
= δ( k |
′ |
|
|
|||
|
|
|
dr |
− k ) , à |
|
||||
− ∞ |
|
|
|
|
|
|
|
|
|
′ |
|
r |
|
|
|
|
|
|
|
и переобозначив k = q , получаем |
|
||||||||
) r |
|
i |
∞ |
) |
r |
) r |
|
||
r |
|
|
|
r r |
|
r r |
|
||
∂t v( k ) + |
|
|
ò[ v( q )( k |
− q )]v( k |
− |
||||
|
8π 3 |
||||||||
|
|
|
− ∞ |
|
|
|
|
|
|
∞ r |
r |
|
r r |
r |
¢ |
¢ |
¢ |
||
òf (k )δ(k |
- |
k )dk |
= f (k ) , |
|
− ∞
r r |
|
− 1 |
r r |
) |
r |
) r |
= − iρ |
) |
2 r |
|
f ( k ). |
||
q )dq |
|
kp( k ) − νk |
v( k ) + |
|||
(4.12)
Уравнение неразрывности (4.2) в пространстве Ф урье имеет простой
âèä
r |
(4.13) |
k ×v( k ) = 0 |
и может быть использовано для исклю чения из уравнения (4.12) члена с
давлением. Умножение (4.12) на k |
с учетом (4.13) приводит к выражению |
||||||||||
) |
r |
− k |
∞ ) |
r |
r |
) r |
r r |
ik |
|
) r |
|
|
r r |
|
r |
|
|
|
|||||
ρ − 1 p( k ) = |
|
ò[ v( q )( k − q )]v( k |
− q )dq − |
|
|
f ( k ) . |
(4.14) |
||||
8π 3k 2 |
k 2 |
|
|||||||||
|
|
|
− ∞ |
|
|
|
|
|
|
|
|
П одставляя (4.14) в (4.12) и используя |
|
|
r |
|
r |
rr r r |
|||||
формулу a |
´(b ´c ) = b (ac) - c(ab ) äëÿ |
||||||||||
объединения нелинейных членов, приходим к уравнению
|
) |
r |
|
i |
|
∞ |
|
r |
r |
) |
r |
|
|
r |
|
|
|
|
[ k × ( v( k − |
q ) × k )] |
r r |
|
|
||
|
∂t v( k ) + |
|
|
|
|
|
|
|
[ v( q )( k |
− |
||
|
|
8π 3 |
ò |
k 2 |
|
|||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
− ∞ |
|
|
|
|
|
|
ãäå |
r r |
|
r |
r |
|
r |
|
|
|
|
||
f ' ( k ) = k − 2 [ k ´( |
f ´k )] . |
|
|
|
|
|||||||
r r |
) |
r |
) r |
|
r |
|
f ' ( k ) , |
(4.15) |
|
q )]dq |
= − νk 2 v( k ) + |
|||
Ц елью проводимых преобразований являетсяуравнение для энергии, заклю ченной в данных масш табах (волновых числах), которая получается путем интегрирования квадрата модуля фурье-компонент поля скорости по всем волновым векторам сзаданным значением модуля | k |= k :
r |
|
E( k ) = rò|rv( k )|2 dk . |
(4.16) |
k =|k|
